Electrónica, Electricidad y Sonido
Modelado difuso de planta no lineal
“Modelado Difuso de Planta no lineal MIMO”
Extracto
Se modelará un sistema MIMO de dos entradas y dos salidas no lineal usando linealizaciones en puntos específicos, que se unirán a través de un sistema desdifusificador, para generar el modelo. Es sistema es un estanque mezclador con dos flujos de entrada y un flujo de salida, que posee una concentración de un soluto. El modelado de la dinámica del flujo de salida se consigue en un paso de difusificación, y el de la concentración se logra a través de dos en serie.
Introducción
En el ramo de control multivariable se enseña una gran cantidad de aproximaciones al control de sistemas multivariables lineales, que incluyen formas de controlar los errores debidos a la inexactitud del modelado. Sin embargo, hay casos donde no se puede aplicar un modelo lineal para caracterizar un sistema, normalmente porque las entradas y salidas no mantienen niveles estables que puedan ser considerados como puntos de equilibrio para linealizar, o a menos, en la operación normal se alejan de estos lo suficiente como para que el modelado no sea válido. En este trabajo se modelará un estanque mezclador cilíndrico[1] que posee dos flujos de entrada, cada uno con concentraciones molares constantes distintas de un soluto, que no alcanzan a modificar la densidad del líquido que lo transporta, y dos salidas: un flujo de salida, provocado sólo por diferencia de presiones, y la concentración del soluto saliente, que se considerará igual a la que se encuentra en el interior del estanque.
Modelo no lineal
Las ecuaciones que modelan el proceso son:
| Parámetro | Descripción | Valor | Unidad |
| f1(t) | Flujo de entrada 1 | - | [m3/s] |
| f2(t) | Flujo de entrada 2 | - | [m3/s] |
| f(t) | Flujo de salida | - | [m3/s] |
| c1 | concentración de entrada 1 | 1 | [mol/m3] |
| c2 | concentración de entrada 2 | 2 | [mol/m3] |
| c(t) | concentración de salida | - | [mol/m3] |
| V(t) | Volumen del líquido | - | [m3] |
| k | Constante de salida | 0.02 | [m1/2/s] |
| A | Área basal del cilindro | 1 | [m2] |
El modelo incluye tres tipos de no linealidades: La división para despejar c(t), la raíz que relaciona V(t) con f(t) y las saturaciones, que se incluirán en el diagrama Simulink a las variables, ya que ninguna puede presentar valores negativos, por definición.
Modelo lineal
Lo siguiente es explicado en detalle en la bibliografía, de donde se tomó el ejemplo, aunque se haga uso de una definición levemente distinta, pero equivalente. Definimos las variables como variaciones en torno a sus puntos de equilibrio:
Hacemos cero las derivadas del sistema, para hallar los puntos de equilibrio:
Definimos como variables de estado a y . Reemplazamos f0 y linealizamos el sistema:
Se observa que la concentración puede ser medida directamente en la salida, y el volumen puede ser medido, o se lo puede calcular con una relación algebraica. Esto facilita bastante el diseño, pues no se requiere de un observador del estado.
Validez del modelo lineal
Se implementa el sistema no lineal en Simulink, y se compara con la salida entregada por una realización lineal. Se ocupa un sistema lineal que supone puntos de equilibrio de y . Se ingresan señales sinusoidales que hacen que el volumen del mezclador varíe entre 0 y 4 [m3] y la concentración entre 1 y 2 [mol/m3]. Al alejarse del punto de equilibrio se notan los errores, imperceptibles en sus vecindades.
Figura 1: Flujo en zona no lineal
Figura 1: Concentración en zona no lineal
El error es más claro en la concentración, pues ésta no puede pasar más allá de los límites que le imponen las concentraciones de entrada. Se comprueba que un único modelo lineal de este sistema no podrá entregar información fidedigna su estado.
Modelado Difuso
Flujo
Comenzaremos difusificando la descripción del flujo, pues su dinámica no depende de la otra variable de salida. Al observar las ecuaciones linealizadas se ve que los valores de las componentes de las matrices dependen del punto de equilibrio de la raíz del volumen contenido, por lo que es natural difusificar usándolo como parámetro. Este puede ser obtenido midiendo la altura del líquido en el estanque, o calculado desde el flujo de salida.
Supondremos que el volumen del estanque tiene un rango de trabajo que va desde 1 a 3 [m3]. Se calculan la descripción lineal para el sistema para V0 igual a 0.5, 1, 2 y 4 [m3]. El sistema no puede ser linealizado en cero, pues en ese punto no es derivable, por lo que se hace una linealización en un punto cercano, V0 = 0.01, y se ocupa como si fuera la correcta.
Se escogen conjuntos difusos definidos por tramos, de modo que siempre sumen uno, y no haya que calcular el factor de ajuste. De esta manera la salida del sistema siempre es una ponderación de dos de los sistemas lineales.
Figura 3: Funciones de pertenencia del flujo
Para conseguir la salida simplemente se multiplica la función de pertenencia con el modelo que le corresponde, y luego se suma con todas las otras salidas del sistema..
El valor del volumen se toma del sistema no lineal original, pero puede ser la misma salida del sistema. La respuesta encontrada es la siguiente:
Figura 4: Flujo del Sistema Difuso
El sistema presenta aún errores, pero son mucho menores que los que se obtienen al aplicar sólo una aproximación lineal al sistema.
Concentración
En la transferencia lineal se observa que la concentración depende del valor del flujo para calcularse, por lo que no es suficiente con sólo un sistema difuso para calcular ambas. Para solucionar este problema se generan grupos de aproximaciones difusas del sistema que aproximen el flujo y la concentración para distintos pares de puntos de equilibrio de las entradas.
Primero se linealizó para c0 igual a 1; 1.5 y 2 [mol/m3], y para cada valor de V0 ocupado en el paso anterior. Se agrupó la salida de los módulos con igual c0 y se desdifusificó, hallándose que la salida no era muy satisfactoria, pues se salía de los rangos permitidos para la concentración, pues en el modelo que se usó no se incluía la limitación específica de que la concentración estaba acotada. Abandonamos ese camino, y luego se linealizó de manera similar, en c0 igual a 1.25; 1.5 y 1.75 [mol/m3], y en las fronteras se remplazó el modelo por el valor constante que toma la concentración en estos puntos. Los resultados fueron medianamente satisfactorios, pues la salida se aproximaba a los valores de cota demasiado rápido, aunque el modelado de la zona media era satisfactorio.
Figura 5: Concentración difusa, salida real punteada
Figura 6: Funciones de pertenencia
Se generó otro modelo, ahora aplicando linealizaciones en los puntos de la frontera, y se incluyó también los valores constantes para la salida de las cotas, pero con funciones de pertenencia nítidas, que después de todo son un subconjunto de las difusas.
Figura 7: Funciones de pertenencia
Así al retroalimentar la salida de la planta difusa como parámetro para difusificar, la planta debería saber que fuera de los límites de la zona permitida no hay variación en la concentración. Lamentablemente, la planta al generar salidas fuera del rango efectivamente entregaba una salida constante, pero esto impedía el cambio de representación, y la salida se mantenía siempre en el mismo valor.
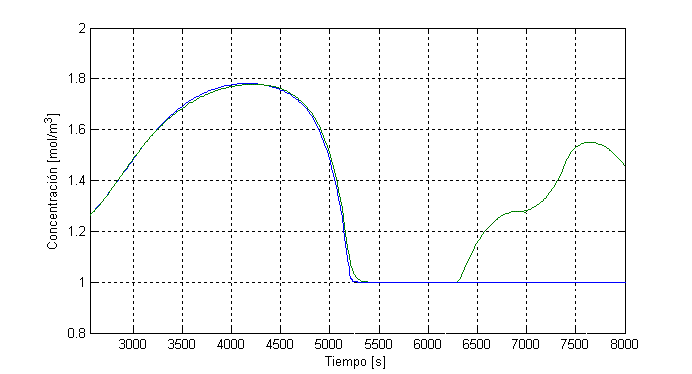
Figura 8: Salida del sistema difuso retroalimentado con lógica nítida
Se probó un tercer esquema, donde se aplicó las funciones de pertenencia de la figura 6, y simplemente se saturó la salida entre 1 y 2, externamente. Se logró una mejora sustancial, como puede apreciarse en la siguiente figura:
Figura 9: Salida del sistema difuso saturado
Cabe destacar que en el diseño del modelo de la concentración no hubo que alterar el que aproximaba al flujo. Se obtuvo errores bajos por separado, y se logró cubrir los rangos completos de trabajo describiendo de buena manera la dinámica MIMO del sistema, donde los estados interactúan entre ellos.
Conclusiones
Las descripciones lineales son válidas sólo en vecindades de los puntos donde se calculó la linealización, por lo que se debe revisar la validez del modelo al ocuparlo para diseñar un sistema de control.
El aplicar un modelado difuso permite aumentar el rango donde el sistema se asemeja al original. Esto presenta la ventaja de que se puede modelar un sistema no lineal complejo sólo caracterizando las partes de mayor importancia, y luego uniendo las descripciones por un sistema difuso.
Es útil en algunos casos mezclar lógica difusa con lógica nítida, sobre todo cuando las discontinuidades que se desea modelar son muy bruscas, no derivables, donde un cambio de descripción pausado no funciona.
Puede controlarse ahora el sistema usando un control lineal diseñado para cada caso en particular. La salida del control se encontraría difusificando y desdifusificando de la misma manera que se hizo para encontrar el modelo. El único inconveniente es que se tiene cinco puntos de equilibrio de la concentración por cada uno de los cinco puntos de equilibrio del flujo. Un método de facilitar esto es diseñar utilizando Matlab el filtro de Kalman para cada caso [2]. Esto nos entrega un arreglo matricial con componentes constantes, que presenta menos problemas para difusificar.
Referencias
Kwakernaak H., Silvan R. “Linear Optimal Control Systems”, Ejemplo 1.2 págs. 7-10
[2] Maciejowski J. M. “Multivariable Feedback Design”, capítulo 5, págs 223-230
Anexo: Diagramas Simulink
Sistema no lineal:
Sistema lineal:
Funciones de pertenencia del Flujo:
Control Multivariable, Segundo Semestre 2006
9
|
| UNIVERSIDAD TÉCNICA FEDERICO SANTA MARÍA DEPARTAMENTO DE ELECTRÓNICA |
|
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | Chile |


