Ingeniero Industrial
Métodos numéricos
PRÁCTICA NO. 1
1 Hallar la raíz de la función f(x)=0, aplicando el método de la bisección, sí:
f(x)=ln(x)-5+x con un error de 0,00001
2 Encontrar las dos raíces de la ecuación: ![]()
con una aproximación de ![]()
por cualquier método.
3 Hallar la raíz de la ecuación y=senx+lnx+5 por cualquier método con una aproximación de 0,00001.
4 Con el método de la Regula Falsi resolver la ecuación y=tan(x)-1-x, en el intervalo ![]()
.
5. Halle una raíz positiva mayor a 1 de la siguiente ecuación: ![]()
.
6 La ecuación del movimiento de un proyectil en función del tiempo viene dada por: 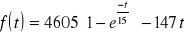
determine el tiempo transcurrido hasta el momento del impacto, con seis cifras de aproximación.
7 De una lámina metálica o plancha que mide 10 dm x 16 dm se desea construir una caja sin tapa. ¿Cuál debe ser, en dm el lado de los cuadrados que hay que recortar en cada esquina para que el volumen de la caja sea 100 dm3?. El instrumento con el que se medirán los lados de los cuadrados tiene una precisión de 0,01 mm.
8 Si deseásemos resolver ecuaciones no lineales por el método de Newton Raphson de tercer orden, ¿Cuál sería el algoritmo a emplear?. (Utilizar la serie de Taylor).
9 Resolver por el método del Punto Fijo la ecuación ![]()
con E=0,0001.
Nota. Resolver solo 6 problemas, entre ellos el 7 y el 8.
Descargar
| Enviado por: | Micky |
| Idioma: | castellano |
| País: | Bolivia |
