Matemáticas
Método de Simpson
MÉTODO DE SIMPSON.
Cálculo de áreas:
Uno de los problemas matemáticos más frecuentes es el cálculo del área que se forma al graficar una función. Por ejemplo, se necesita calcular el área A que aparece en la siguiente figura:
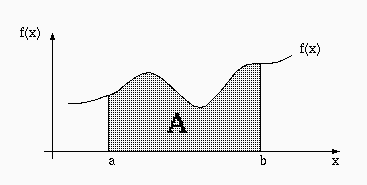
en donde la función f(x) y los valores a y b son conocidos.
En este tipo de problemas se pueden obtener dos tipos de soluciones:
-
Soluciones algebraicas: se obtiene una fórmula precisa y exacta para el área solicitada.
-
Soluciones numéricas: se calcula numéricamente una estimación del área.
Desde luego, la soluciones algebraicas son mejores que las numéricas, porque son exactas. Pero a veces, la complejidad de las funciones hace imposible (o difícil) obtener la solución algebraica, por lo que una solución numérica permite ahorrar tiempo.
El método de Simpson.
En este procedimiento, se toma el intervalo de anchura 2h, comprendido entre xi y xi+2, y se sustituye la función f(x) por la parábola que pasa por tres puntos (xi, yi), (xi+1, yi+1), y (xi+2, yi+2). El valor del área aproximada, sombreada en la figura, se calcula con un poco más de trabajo y el resultado es
![]()
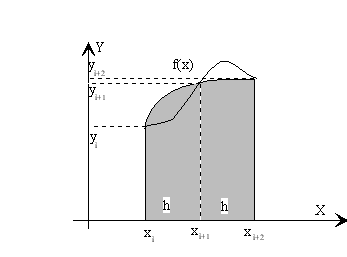
La simple inspección visual de esta figura y la que describe el fisica/cursoJava/numerico/integracion/trapecio/trapecio.htm">procedimiento de los trapecios nos confirma que el método de Simpson deberá ser mucho más exacto que el procedimiento del trapecio. El área aproximada en el intervalo [a, b] es
![]()
bien, agrupando términos
![]()
El primer paréntesis, contiene la suma de los extremos, el segundo, la suma de los términos de índice impar, y el tercero la suma de los términos de índice par. En el método de Simpson, el número de divisiones n debe de ser par. En el caso de que el usuario introduzca un número impar el programa lo convierte en el número par siguiente.
Ejemplo: Usando la regla de Simpson con n=2 y n=4 aproximamos:
![]()
cuyo valor exacto es ![]()
correcto al número de cifras mostradas. Para n=2 tenemos que h=(2-1)/2=0.5, x0=1, x1=1.5, x2=2. Ahora
![]()
Con n=4 tenemos h=(2-1)/4=0.25, x0=1, x1=1.25, x2=1.5, x3=1.75, x2=2, de modo que
![]()
Obtuvimos los siguientes resultados:
| n | Sn(f) | en=I(f)- Sn(f) | en/ e2n |
| 2 | 0.694444 | -0.00129726 | ----- |
| 4 | 0.693254 | -0.000106788 | 12.1481 |
| 8 | 0.693155 | -7.35009e-006 | 14.5288 |
| 16 | 0.693148 | -7.35009e-006 | 14.5288 |
| 32 | 0.693147 | -2.97299e-008 | 15.885 |
| 64 | 0.693147 | -1.86151e-009 | 15.9708 |
| 128 | 0.693147 | -1.16398e-010 | 15.9927 |
| 256 | 0.693147 | -7.27562e-012 | 15.9983 |
| 512 | 0.693147 | -4.54747e-013 | 15.9993 |
| 1024 | 0.693147 | -2.84217e-014 | 16.0000 |
Estos resultados confirman claramente la convergencia de la regla de Simpson en este ejemplo particular. Podemos ver que cada ves que se duplica la n, lo cual equivale a dividir la h entre dos, el error disminuye por un factor de 16 aproximadamente (última columna de la tabla) esto es característico de convergencia O(h4) lo cual confirmaremos teóricamente más adelante.
INICIO
Dame el limite inferior, superior, y la
precisión n par
a, b, n
i=1; i<=2*n-1; i=i+2
i=2; i<=2*n-2; i=i+2
RESULTADO
at
FIN
Flotantes: at, si, sp, a, b, h, x, ya, yb, s, y, f();
Enteras: i, n;
h=(b-a)/(2*n);
ya = f(a);
yb = f(b);
si=0;
x=a+i*h;
y=f (x);
si=si+y
sp=0
x=a+i*h;
y=f(x);
sp=sp+y;
at=h/3*(ya+yb+4*si+2*sp);
Descargar
| Enviado por: | Jose Arturo Hernández Cruz |
| Idioma: | castellano |
| País: | México |
