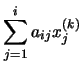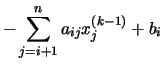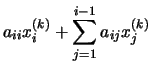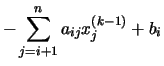Matemáticas
Método de Gauss-Seidel y Newton
Método de Gauss-Seidel
La iteración de Gauss-Seidel se define al tomar Q como la parte triangular inferior de A incluyendo los elementos de la diagonal:

Si, como en el caso anterior, definimos la matriz R=A-Q

y la ecuación (63) se puede escribir en la forma:
Qx(k) = -Rx(k-1) + b
Un elemento cualquiera, i, del vector Qx(k) vendrá dado por la ecuación:
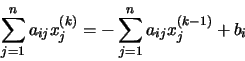
Si tenemos en cuenta la peculiar forma de las matrices Q y R, resulta que todos los sumandos para los que j > i en la parte izquierda son nulos, mientras que en la parte derecha son nulos todos los sumandos para los que ![]()
. Podemos escribir entonces:
|
| = |
|
|
|
| = |
|
|
de donde despejando xi(k), obtenemos:
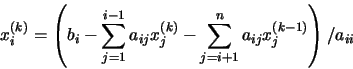
Obsérvese que en el método de Gauss-Seidel los valores actualizados de xi sustituyen de inmediato a los valores anteriores, mientras que en el método de Jacobi todas las componentes nuevas del vector se calculan antes de llevar a cabo la sustitución. Por contra, en el método de Gauss-Seidel los cálculos deben llevarse a cabo por orden, ya que el nuevo valor xi depende de los valores actualizados de x1, x2, ..., xi-1.
En la figura (15) se incluye un algoritmo para la iteración de Gauss-Seidel.
| Figure: Algoritmo para la iteración de Gauss-Seidel. |
|
|
Método de Newton
Este método parte de una aproximación inicial x0 y obtiene una aproximación mejor, x1, dada por la fórmula:
| | (29) |
La expresión anterior puede derivarse a partir de un desarrollo en serie de Taylor. Efectivamente, sea r un cero de f y sea x una aproximación a r tal que r=x+h. Si f'' existe y es continua, por el teorema de Taylor tenemos:
| 0 = f(r) = f(x+h) = f(x) + hf'(x) + O(h2) | (30) |
en donde h=r-x. Si x está próximo a r (es decir hes pequeña), es razonable ignorar el término O(h2):
| 0 = f(x) + hf'(x) | (31) |
por lo que obtenemos la siguiente expresión para h:
| | (32) |
A partir de la ecuación (32) y teniendo en cuenta que r=x+h es fácil derivar la ecuación (29).

| Figure: Interpretación geométrica del método de Newton. |
| [scale=0.9]eps/new-1 |
El método de Newton tiene una interpretación geométrica sencilla, como se puede apreciar del análisis de la figura (6). De hecho, el método de Newton consiste en una linealización de la función, es decir, f se reemplaza por una recta tal que contiene al punto (x0,f(x0)) y cuya pendiente coincide con la derivada de la función en el punto, f'(x0). La nueva aproximación a la raíz, x1, se obtiene de la intersección de la función linear con el eje X de ordenadas.
Veamos como podemos obtener la ecuación (29) a partir de lo dicho en el párrafo anterior. La ecuación de la recta que pasa por el punto (x0,f(x0)) y de pendiente f'(x0) es:
| y - f(x0) = f'(x0)(x-x0) | (33) |
de donde, haciendo y=0 y despejando x obtenemos la ecuación de Newton-Raphson (29).

| Figure: Dos situaciones en las que el método de Newton no funciona adecuadamente: (a) el método no alcanza la convergencia y (b) el método converge hacia un punto que no es un cero de la ecuación. |
| [scale=0.9]eps/new-2 |
El método de Newton es muy rápido y eficiente ya que la convergencia es de tipo cuadrático (el número de cifras significativas se duplica en cada iteración). Sin embargo, la convergencia depende en gran medida de la forma que adopta la función en las proximidades del punto de iteración. En la figura (7) se muestran dos situaciones en las que este método no es capaz de alcanzar la convergencia (figura (7a)) o bien converge hacia un punto que no es un cero de la ecuación (figura (7b)).
Algoritmo de Newton
Por ser el más sencillo de implementar, comenzaremos con este algoritmo. Supongamos que queremos hallar la raíz de la función f(x)=cos2(2x)ðx2 en el intervalo [0,1.5].
Calcule la derivada fð(x) y encuentre una expresión para la función g(x)=xðf(x)/fð(x).
Escriba una función de MATLAB llamada pfijo que ejecute la iteración de punto fijo con g. Su estructura debe ser aproximadamente
function [y]=pfijo(x)
y=x-...
donde x es el valor de entrada, e y=g(x). Recuerde salvar la función con el nombre pfijo.m. Pruebe con distintos valores de x a ver si pfijo funciona correctamente.
Implemente la función mi_newton que realice la iteración de Newton para f. La misma debe contener el llamado a la función pfijo (tantas veces como sea necesario):
function [y,iter]=mi_newton(x0,tol)
y=pfijo(x0);
...;
donde x0 es el valor inicial x(0), y la salida consta del valor y=x(k) que aproxima a la raíz r, y el valor iter que contiene la cantidad de iteraciones realizadas. Como criterio de parada escoja que
| ðx(k)ðx(kð1)ð < tol |
Se sugiere usar para ello un ciclo while con el formato
while abs(...)>=tol,
...; iter=iter+1; end
Asegúrese de que la función está trabajando correctamente.
Con la tolerancia en el error absoluto tol=10ð10 encuentre experimentalmente las regiones I ð R tales que para x(0) ð I, la iteración de Newton converge a la raíz r ð 0.5149.
La función
| F(x)=exð 1 sinx | (1) | |||
tiene dos raíces positivas, una de las cuales está muy cerca de un punto singular. Modifique las funciones elaboradas anteriormente para que pueda calcular esas dos raíces.
UNIVERSIDAD AUTONOMA DE NUEVO LEON
FIME
ANÁLISIS NUMERICO
INVESTIGACIÓN METODOS DE GAUSS Y NEWTON
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | México |