Mecánica de fluidos. Coordenada en una superficie curva
Dinámica medios continuos. Fuerza, densidad, gravedad. Línea de acción. Momento. Centroide
- Mecánica de fluidos. Coordenada en una superficie curva
Ficha resumen del documento - Mecánica de fluidos. Coordenada en una superficie curva
Versión PDF - Mecánica de fluidos. Coordenada en una superficie curva
Versión para descargar
LINEA DE ACCION DE LA COMPONENTE VERTICAL
SOBRE UNA SUPERFICIE CURVA
Para darle respuesta a esta pregunta, debemos saber primero cual es la magnitud de la fuerza Vertical:
Pero recordemos que el diferencial de Fuerza (dF) es igual a la Presión (P) multiplicada por el diferencial de Area (dA) (dF=PdA).
También Sabemos que la Presión (P) es igual a la Densidad (ρ) multiplicada por la Gravedad (g) multiplicada por la Altura (h). (P= ρgh).
Además conocemos que dAsenððdAx
Y también hdAx = dV
Integrando ambos lados de la Ecuación Tenemos:
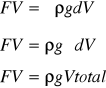
Y Además la masa (m) es igual a la Densidad (ρð por el Volumen Total (Vtotal).
(m= ρVtotal).
Lo que representa la Componente Vertical de la
Fuerza Hidrostática sobre una Superficie Curva.
Ahora bien la Línea de Acción de esta componente de la fuerza estará ubicada o más bien pasara a través del Centroide del Volumen en cuestión, extendiéndose por encima de la superficie curva hasta la superficie libre. Las Coordenadas del Centroide serian (
).
Si esta componente realiza o tiene un momento con respecto a un eje escogido convenientemente tendremos:
Donde 
será la distancia desde el origen o punto donde queremos verificar el momento hasta la Línea de Acción de la Fuerza Vertical.
Siendo el Momento de la Fuerza Resultante:
Igualamos estos Momentos y tenemos:
Recordemos que cuando hablamos de Integrales, hablamos también de Sumatorias (ð), lo que significa que:
puede expresarse como:
