Tecnología
Lógica
Introducción.
Con el pasar de los años el hombre siempre a querido buscar la manera de explicar en totalidad los fenómenos que ocurren en la naturaleza, desde la propia vida, hasta la creación del universo.
A partir de estas inquietudes, importantes ciencias han nacido, como la física, la química y la matemática por nombrar algunas, las cuales de una u otra forma han logrado, pero no en su totalidad satisfacer la curiosidad humana; estas grandes ciencias han dado pasos importantes con la ayuda de un gran aliado “La lógica”, la cual a brindado caminos para la expansión y explotación de dichas ciencias.
La lógica con el pasar de los años ha tenido una gran participación en grandes descubrimientos como ha sido la tabla periódica, creada por el ruso Dimitri Mendeleiev en 1869, o el álgebra de Boole el cual con su aporte abrió las puertas a un gran campo de la ingeniería digital como es la electrónica digital y otras, o los trabajos de Herbrand en 1930 quien presento un algoritmo para encontrar, una interpretación que pueda facilitar una formula.
Como nos podemos dar cuenta la lógica ha logrado conquistar el extenso mundo de la investigación y lo seguirá conquistando hoy, mañana y siempre.
Lógica: la lógica se puede definir como una disciplina que investiga y estudia los principios formales del conocimiento humano, y su concordancia consigo mismo, se decir, las formas y las leyes mas generales del pensamiento humano considerado puramente en si mismo sin referencia a los objetos.
A mediados del siglo pasado un hombre desarrollo una teoría matemática distinta a la que entones se conocía y cuya expansión ha sido tan rápida que en la actualidad se aplica a la resolución de mayorías de operaciones industriales complejas; este hombre fue George Boole el creador del álgebra que lleva su mismo nombre.
El álgebra de Boole establece una serie de postulados y operaciones lógicas, que consisten en admitir dos estados donde dichos estados tienen un carácter opuesto. Así, por ejemplo, a una lámpara corriente (tubo fluorescente) el álgebra de Boole sólo la considera en uno de los dos estados posibles y opuestos: encendida o apagada. No se admiten estados intermedios. A uno de los dos estados posibles (lámpara encendida), se le denomina de diversas formas tales como: Verdadero, Estado Alto, Nivel Lógico 1, etc. Al otro estado (lámpara apagada), se le referencia con palabras opuestas tales como: Falso, Estado Bajo, Nivel Lógico 0, etc.
La posibilidad de que todos los elementos admitan dos estados en este "Tipo de Álgebra" ha llevado a llamarla "álgebra binaria". La denominación de "álgebra lógica" se debe al carácter intuitivo y lógico que tienen los razonamientos que en ella se aplican.
En la implementación de las ecuaciones lógicas que resuelven los procesos en los que se aplica el álgebra de Boole, se utilizan diversas operaciones o funciones lógicas entre las que se citan las tres fundamentales:
Función AND o producto lógico.
Función OR o suma lógica.
Función NOT o negación lógica.
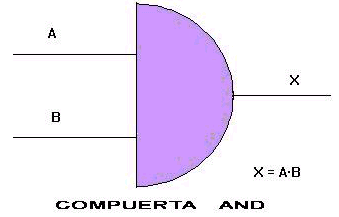
Función Lógica AND. Puerta AND:
La operación lógica AND, producen una variable de salida, que sólo toma el nivel lógico 1 o estado alto o verdadero, si todas ellas tienen dicho nivel o estado.
La operación lógica AND también recibe el nombre de producto lógico porque se representa mediante un punto, igual que la operación convencional de multiplicación.
La expresión simbólica de dicha ecuación en el álgebra de Boole es la siguiente:
Ecuación lógica de la función AND para dos variables de entrada
X = A · B
Para representar una ecuación lógica de forma clara y completa se usa un gráfico denominado Tabla de Verdad, que consiste en una tabla cuyas columnas de la parte izquierda representan todas las combinaciones posibles que pueden tomar las variables de entrada. En la columna derecha se indica el valor que toman las salidas para cada combinación de las entradas. En el caso de la ecuación X = A · B, existen dos entradas (A, B) y un sola salida (X). El número de combinaciones diferentes, N que se pueden realizar con a variables binarias viene expresado por la fórmula N = 2ª , que en el ejemplo citado, dará lugar a N = 2 x 2 = 4 combinaciones posibles. En consecuencia, la tabla de verdad dispondrá de 4 combinaciones diferentes para las dos entradas y, para cada una de ellas, (en la columna de la derecha) se expresará el valor que toma la salida tal como se expresa a continuación:
Tabla de verdad que describe la ecuación lógica X = A . B
| VALOR EN LA PARTE A | VALOR EN LA PARTE B | VALOR OBTENIDO EN LA SALIDA |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Representación Grafica de la Compuerta
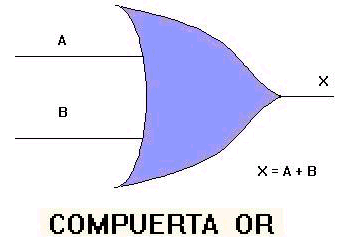
Función Lógica OR ó Puerta OR:
Cuando distintas variables lógicas se combinan mediante la función OR, el resultado toma el estado ALTO si alguna de ellas tiene dicho estado.
La operación OR es menos exigente que la AND por que sólo exige que alguna de las variables de entrada valga 1, para que la salida tome ese nivel. A la función OR también se le denomina Suma Lógica ya que se representa con el símbolo suma (+). En castellano recibe el nombre de operación O, puesto que la salida vale sólo 1 solo si presenta dicho valor la entrada A "o" la B. La ecuación que representa la función OR de dos variables de entrada es la siguiente:
A continuación se representa la tabla de verdad que representa a la ecuación anterior.
Ecuación lógica de la función OR para dos variables de entrada
X= A + B
| VALOR EN LA PARTE A | VALOR EN LA PARTE B | VALOR OBTENIDO EN LA SALIDA |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Representación Grafica de la Compuerta
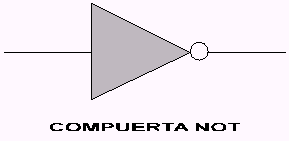
FUNCION LÓGICA NOT. PUERTA NOT O INVERSOR
Se trata de una operación que sólo maneja una variable de entrada y otra de salida. La salida toma el estado opuesto o inverso del que tiene la entrada. Por este motivo, también se le llama Función Inversión o negación. En castellano recibe el nombre de operación NO.
La siguiente figura muestra la ecuación lógica de la función NOT, su tabla de verdad y el símbolo usado para la representación de la puerta NOT.
Tabla de Verdad de la Puerta Inversora NOT
| Entrada | Salida |
| 0 | 1 |
| 1 | 0 |
Representación Grafica de la Compuerta
Utilidad del Álgebra de Boole
La lógica binaria a dado un gran aporte a los circuitos lógicos porque es lo mas sencillo de manejar ya que en la lógica binaria solamente hay dos posibles estados; Cero o Uno (un 1 equivale a 5 voltios) o es un cero (un 0 como lo indica su nombre tiene un valor de cero voltios) y esto nos simplifica el trabajo, pues con sólo dos estados posibles son menos variables las que debemos de tomar en cuenta al realizar diseños, pudiendo realizarlos desde una complejidad mínima hasta una complejidad considerablemente alta.
El álgebra Booleana se aprovecha para expresar y simular los efectos que los diversos circuitos digitales ejercen sobre las entradas lógicas, y para manipular variables lógicas con el objeto de determinar el mejor método de ejecución de cierta función.
Ya que sólo puede haber dos valores, el álgebra Booleana es relativamente fácil de manejar, comparándola con el álgebra ordinaria. En el álgebra Booleana, no hay fracciones, números negativos, raíces cuadradas, raíces cúbicas, logaritmos, números imaginarios ni nada de esas operaciones que empleamos en el álgebra decimal.
INTENTO DE CLASIFICACIÓN DE LOS ELEMENTOS
En la Edad Media, los alquimistas, los antecesores de los químicos, tenían como meta fundamental modificar su ser interior para alcanzar un estado espiritual mas elevado y pensaban que con la transmutación de los metales en oro podían lograrlo. Esa transmutación, conocida como la gran obra, debía realizarse en presencia de la piedra filosofal, cuya preparación fue la tarea que se impusieron los alquimistas. En el siglo XIII, el objetivo de la alquimia incorporo la búsqueda del elixir de la larga vida, infusión de la piedra filosofal, que debía eliminar la enfermedad y prolongar la vida.
El primer intento de clasificación se baso en separar los elementos en 2 grupos. Los elementos que tenían características metálicas y los que no las tenían, es decir; separaron los metales de los no metales. Sin embargo, este primer intento de clasificación no resulto satisfactorio ya que quedaban agrupados elementos muy diferentes y además no podía establecerse una separación clara entre ambos grupos ya que algunos elementos presentaban a la vez características metálicas y no metálicas.
En 1829 el químico alemán Dôbereiner observó que había serie de tres elementos, que denominó tríadas, que presentaban propiedades muy similares. Así, por ejemplo: Li, Na, K; Ca , Sr, Ba; Cl, Br , I; etc. Además, se cumplía que la masa atómica del elemento central de la tríada era prácticamente la media aritmética de las masas atómicas de los elementos de los extremos. En efecto, si consideramos la tríada formada por Li, Na , K, las masas atómicas respectivas son 7,23, y 39. Puede comprobarse con facilidad que (7+ 39):2 = 23. Sin embargo, no todos los elementos podían clasificarse de este modo.
En 1830 el químico John Jacob Berzelius propuso un método para representar los elementos: utilizar la inicial del nombre en latín o en todo caso la inicial seguida de otra letra presente en el nombre latino si dos o mas elementos tenían la misma inicial, por ejemplo: N(Nitrógeno), Na(Sodio), Ni(Níquel). Actualmente se sigue empleando esta simbología.
En 1864 el químico John Newlands ordenó los elementos entonces conocidos en orden de masa atómicas crecientes. Newlands observó que al ordenar los elementos de este modo, cada siete elementos consecutivos tenían propiedades diferentes pero el octavo elemento tenía propiedades similares a las del primer elemento del grupo anterior. Hoy en día se conoce este intento de clasificación como ley de las octavas de Newlands. El problema que se le planteaba a Newlands es que su ley tan solo funcionaba correctamente para dos octavas; en la tercera octava y en las siguientes no se verificaba.
Entre 1868 y 1870 los trabajos de Meyer y Mendeleiev los llevaron a clasificar los elementos atendiendo a sus propiedades físicas y químicas. Meyer ordeno los elementos por orden creciente de los pesos atómicos y los relaciono con el volumen atómico en función de los pesos atómicos. En el gráfico se formaban una serie de picos máximos, que correspondían a aquellos grupos con propiedades similares, cada pico constituía un período de la tabla de elementos.
Mendeleiev publico sus resultados en 1870. Una vez ordenados los elementos por peso atómico, estudio sus propiedades químicas en especial en cuanto a sus valencias. Observo que los primeros elementos de la lista mostraban un cambio progresivo en sus valencias, con valores crecientes y decrecientes, estableció así periodos. Los elementos de una misma fila horizontal constituyen un período. Cada período empieza por un metal alcalino y termina con un gas noble. La genialidad y osadía de Mendeleiev se pusieron de manifiesto al dejar espacios vacíos para formar grupos de elementos con las mismas propiedades y predijo las propiedades de los elementos que ocuparían esos lugares vacantes una vez descubiertos. Les dio un nombre provisorio compuesto por el nombre del elemento inmediato superior en la tabla y un prefijo que indicaba el numero de espacios hacia debajo de donde se encontraba ese elemento: eka (para un espacio) y dwi (para dos espacios). Como ejemplo tenemos: eka-boro, eka-aluminio, eka-silicio que fueron descubiertos con posterioridad y se conocen actualmente con los nombres de escanio, galio y germanio respectivamente. Mendeleiev predijo una masa atómica, en el caso del germanio, de 72 cuando experimentalmente se ha comprobado que es de 72,6 y una densidad de 5,5 mientras que la hallada experimentalmente es de 5,47.
El sistema de Mendeleiev consiguió un gran éxito y es una herramienta imprescindible para los químicos actuales.
Ventajas del Sistema de Mendeleiev:
Corrigió los pesos atómicos y las valencias de algunos elementos por no tener sitio en su tabla de la forma en que eran considerados hasta entonces.
Señaló las propiedades de algunos elementos desconocidos.
En 1894 Ramsy descubrió un gas el que denominó Argón. Es monoatómico, no presenta reacciones químicas y carecía de un lugar en la tabla. Inmediatamente suposo que debían existir otros gases de propiedades similares y que todos juntos formarían un grupo. En efecto, poco después se descubrieron los otros gases nobles y se les asigno el grupo cero.
Todos los huecos que dejo en blanco se fueron llenando al descubrirse los elementos correspondientes. Estos presentaban propiedades similares a las asignadas por Mendeleiev.
Desventajas del Sistema de Mendeleiev:
No tiene un lugar fijo para el Hidrógeno.
Destaca una sola valencia.
El conjunto de elementos con el nombre de tierras raras o escasas no tiene ubicación en la tabla o es necesario ponerlos todos junto en un mismo lugar, como si fueran un solo elemento, lo cual no es cierto.
No había explicación posible al hecho de que unos períodos contarán de 8 elementos, otros de 18, otros de 32, etc.
La distribución de los elementos no esta siempre en orden creciente de sus pesos atómicos.
La configuración electrónica de cualquier elemento, en el sistema periódico actual, es igual a la del elemento que le precede mas un electrón que recibe el nombre de electrón diferenciador. Esto es así porque al estar ordenados los elementos por números atómicos crecientes cada elemento tiene un electrón mas y un protón mas en el núcleo que el elemento precedente. De este modo, los elementos de cada grupo se caracterizan por la configuraciones electrónicas de sus últimos niveles. Así, los metales alcalinos, es decir, los elementos del grupo 1a se caracterizan porque la configuración electrónica de su ultimo nivel energético es ns1. Análogamente, los elementos alcalinotérreos , es decir, el grupo 2a presenta configuración electrónica ns2 en su último nivel energético. Los elementos térreos, o sea, los del grupos 3b tienen configuración electrónica ns2np1. los elementos carbonoideos, es decir, el grupo 4b se caracterizan por tener configuración electrónica ns2np2 en su ultimo nivel energético. Los elementos nitrogenoideos, o sea, el grupo 5b presenta configuración electrónica ns2np3 en su ultimo energético. Los elementos anfígenos, es decir, los elementos del grupo 6b presentan configuración electrónica ns2np4 en su ultimo nivel energético. Los elementos halógenos, o sea, el grupo 7b presenta configuración electrónica ns2np5 en su ultimo nivel energético. Los gases nobles tienen configuración electrónica ns2np6 en su ultimo nivel energético. Los elementos de transición se caracterizan porque en su configuración electrónica aún no se ha completado el subnivel d del penúltimo nivel. Los elementos de doble transición , es decir, lantánidos y actínidos se caracterizan porque en su configuración electrónica aún no se ha completado el subnivel f del antepenúltimo nivel energético. Así pues, la situación de un elemento en el sistema periódico nos permite deducir una serie de importantes propiedades relacionadas con su comportamiento químico.
Una de las grandes virtudes de la clasificación de los elementos en el sistema periódico es que permite estudiar comparativamente una serie de propiedades de los elementos.
APLICACIONES DE LA LOGICA A LA DEMOSTRACIÓN AUTOMATICA DE TEOREMAS
La lógica de Primer Orden es , en la actualidad, una de las herramientas mas importantes para la solución de problemas.
Aunque el problema de encontrar un procedimiento único para probar la validez de todas las fórmulas del Calculo de Primer Orden, es irresoluble, existen procedimientos de prueba que pueden verificar si una fórmula es valida (cuando efectivamente lo es), aunque no se pueda conocer efectivamente cuando una fórmula es invalida. En virtud de los resultados de Church y Turing, el planteamiento anterior es lo mejor que podemos esperar obtener de un procedimiento de “Demostración Automática de Teoremas”. Los procedimientos de demostración de Herbrand y los basados en resolución, son procedimientos por refutación; es decir, en lugar de probar que una fórmula es valida, se probará que la negación de la fórmula es inconsistente.
Herbrand en 1930 presentó un algoritmo para encontrar una “interpretación” que pueda “falsificar” una fórmula. El método de Herbrand, es la base de muchos procedimientos automáticos de prueba que se usan en la actualidad. Dado un conjunto S de cláusulas, el algoritmo de Herbrand genera una secuencia S'1,S'2,...,S'n de conjuntos de instancias base de S, y prueba sucesivamente la insatisfactibilidad de los conjuntos generados.
Gilmore, en 1960 fue el primero en presentar una implementación en una computadora, del procedimiento de Herbrand, generando los conjuntos S'n,S'1... en donde S'i es la conjunción de todas las instancias base obtenidas de reemplazar “todas” las variables en S, por las constantes del i-esimo nivel del Universo de Herbrand. El universo de Herbrand define lo siguiente: Sea H0un conjunto de constantes que aparecen en S. Si no aparecen constantes en S, entonces H0 consiste de una sola constante, se dice que H0={a}. Para i=0,1,2,..., sea Hi+1, la unión de Hi y el conjunto de todos los términos de la forma fn(t1,...,tn) para todas las funciones N-arias fn de S, donde tj, j=1, ...n son miembros del conjunto Hi. Entonces cada Hi es llamado el conjunto de constantes de nivel i de S y H",o lim Hi es llamado el Universo de Herbrand de S.
i "
Probar la inconsistencia ahora, es asunto de la lógica de proposiciones y Gilmore uso para ello el método multiplicativo (un método para el cálculo de proposiciones).
Davis y Putnam mejoraron el método unos meses después de publicado el trabajo de Gilmore en el mismo año de 1960. dado un conjunto de cláusulas base S, este método esencialmente elimina cláusulas aplicando cuatro reglas de simplificación. Obtiene un conjunto S', y aplicando el teorema de Herbrand se sabe que S' es insatisfactible si y solo si, S es insatisfactible .
El método de resolución de Robinson esta considerado como el precursor de toda una familia de métodos, que hacen uso de los conceptos centrales, pero que, de alguna manera proponen algún refinamiento. Consiste esencialmente en una extensión de la regla de la literal simple de Davis y Putman. Se aplica directamente a cualquier conjunto de cláusulas (no necesariamente cláusulas base), para probar la insatisfactibilidad de S. El aspecto central del método consiste en probar que si S contiene la cláusula vacía, entonces es inconsistente. En caso de que S no contenga la cláusula vacía, entonces es inconsistente. En caso de que S no contenga la cláusula vacía, se intentara derivarla a partir de la cláusulas existente en S. Si la cláusula vacía es derivada de las cláusulas existente, S es inconsistente.
Descargar
| Enviado por: | Galan De La Red |
| Idioma: | castellano |
| País: | Venezuela |
