Desarrollo de productos electrónicos
Lógica digital
MEMORIA DE EJERCICIOS
Lógica Digital
En esta memoria se van a reflejar una serie de ejercicios realizados en clase, tanto en el entrenador, como en el programa Workbench.
Cada ejercicio estará compuesto de tres partes. La primera parte será el enunciado del ejercicio. La segunda estará formada por la resolución del ejercicio, con todos los elementos que se pidan, como son tabla de verdad, funciones simplificadas, esquemas, etc. La tercera y última parte de cada ejercicio, estará formada por una breve explicación de la teoría empleada para la realización de cada ejercicio, y como se ha aplicado al mismo.
Dado que los ejercicios de esta memoria se van a realizar con el programa Workbench, y éste representa las variables negadas de una función con el símbolo de comillas (`) utilizaré el mismo símbolo durante toda la memoria para representar las variables negadas.
Construir mediante puertas los circuitos correspondientes a las siguientes funciones lógicas:
(abc + a'c)d
[a+b(b'+c)]d'
(b+c')[a'+b'(c+d')
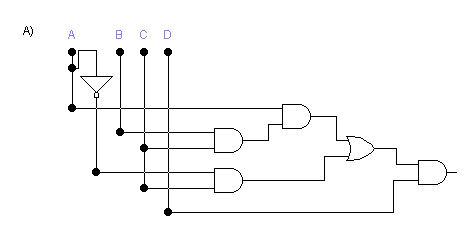
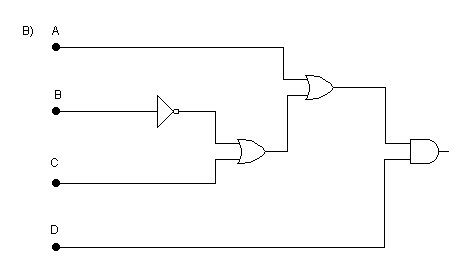
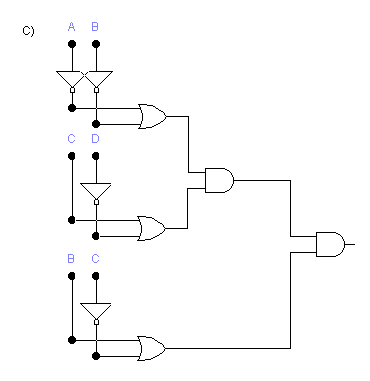
La teoría empleada para la realización de este ejercicio es la de los principios básicos de la electrónica digital, es decir las puertas lógicas. Las puertas lógicas son el dispositivo básico con que se puede montar cualquier circuito. Estas puertas representan dos posibles estados (1 y 0) en los que puede haber o no haber tensión. Pueden ser de diversos tipos, representando cada una de ellas una operación lógica básica.
Puerta NOT o Puerta inversora
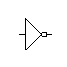
Su función lógica es la de invertir la señal de entrada a la salida. S = A'
Puerta AND o Multiplicación Lógica
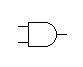
Su función lógica es la de multiplicar sus dos entradas. S = AB
Puerta OR o Suma Lógica
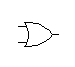
Su función Lógica es la de realizar una suma. S = A + B
Puerta XOR o Suma binaria
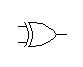
Su función lógica es la de realizar una suma binaria. S = A'B + AB'
Con esta serie de puertas lógicas, se puede implementar cualquier función lógica dada, a partir de esta o de una tabla de verdad.
Todas estas puertas tienen una puerta complementaria, que niega a la salida.
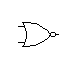
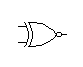
NAND NOR XNOR
Todas estas puertas son la base de la lógica digital, pero actualmente se construyen dentro de un circuito integrado, que está formado por varias de estas puertas.



4 Puertas NAND 4 Puertas NOR 6 Puertas NOT



4 Puertas AND 4 Puertas OR 4 Puertas XOR
Obtener la función y tabla de la verdad de las siguientes figuras:

F = A'B'+A'B+AB'
Tabla de Verdad
| A | B | S |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

F = A'B+AB'
Tabla de Verdad
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
La teoría empleada para realizar este ejercicio es la basada en la obtención de una función y de su tabla de verdad a través del diseño del circuito o viceversa.
En este caso se nos da un diseño de circuito determinado, y a través del mismo, hay que deducir la tabla de la verdad, teniendo en cuenta cómo es el circuito, las puertas lógicas que incluye, y las distintas variaciones a que se somete a las variables. La tabla de verdad es un cuadro formado por tantas columnas como variables tenga la función, y corresponde a la representación gráfica de una función booleana.
Una vez obtenida la tabla de la verdad, habrá que obtener la Función Booleana, que es una variable binaria, cuyo valor depende de una expresión algebraica. Esta función vendrá dada por el número de puertas, y las características de éstas que haya en el diseño del circuito.
Dependiendo del valor de salida que se escoja, esta función se podrá representar de dos maneras, por “producto de sumas” y por “suma de productos” siendo funciones equivalentes. En este caso se ha optado por la suma de productos, y para ello hay que escoger los 1 que hay en la salida, dando como resultado una función que representa el circuito diseñado.
Para realizar una primera selección de ingreso en una determinada empresa, se solicita a los aspirantes que cumplan los requisitos de alguno de los tres puntos siguientes:
-
estar en posesión del título académico y dos años de experiencia en trabajo análogo al ofertado
-
acreditar cinco años de experiencia y vivir en la misma ciudad
-
ser recomendado de la dirección
En todos los casos será necesario tener coche propio.
Obtener la función lógica que relacione adecuadamente todas las variables, y construir un circuito que efectúe automáticamente la selección.
Tabla de Verdad
| A | B | C | D | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Tener coche = A Para ser admitido, tienen que estar
Tener título = B activas al menos la variable A y cualquiera otra.
Tener experiencia = C
Ser recomendado = D
Representación de la función por Suma de productos
F = AB'C'D + AB'CD'+ AB'CD + ABC'D' + ABC'D + ABCD'+ ABCD

La teoría empleada para realizar este ejercicio, está basada de nuevo en las puertas lógicas, pero con variaciones. En este problema nos dan una serie de variables reales, para que a partir de esos supuestos, se construya un circuito electrónico.
El primer paso que se debe seguir, es asignar a cada uno de esos supuestos una letra (A, B, C, D) que serán con las que más adelante construyamos la función. Una vez asignada la letra a cada supuesto, habrá que realizar una Tabla de Verdad.
La Tabla de Verdad es una tabla que incluye tantas variables de entrada y de salida como tengamos. Según las entradas que tengamos, obtendremos una u otra salida. En este caso tenemos cuatro variables de entradas y una única salida y hay que tener en cuenta que tiene que haber siempre una variable activa (en este caso, tener coche) mas una cualquiera de las otras para resultar admitido.
Por tanto, siempre que tengamos un uno en la variable del coche (A) y un uno cualquiera en cualquiera de las otras variables, la salida será un uno. En el caso contrario en que en la variable A tengamos un cero, dará igual cualquiera de las otras variables, puesto que la salida siempre dará como resultado cero.
Una vez obtenida la Tabla de Verdad, con todas sus entradas y salidas, hay que proceder a obtener la función lógica de dicha tabla. Esto se puede realizar de dos maneras, fijándose en los unos a la salida, o en los ceros.
Si nos fijamos en los unos, habrá que sumar todos los productos lógicos para que esa función de cómo resultado uno, obteniendo tantos productos lógicos como unos haya. Cuando una de las variables vale uno, se representa esa variable, pero si la variable vale cero, se representará una variable negada.
Si nos fijamos en los ceros, habrá que multiplicar todas las sumas lógicas para que el resultado final de la función sea 0, obteniendo tantas sumas lógicas como 0 haya. Al igual que en el caso anterior cuando la variable aparece en forma de 0, se representará esa variable, pero si la variable aparece en forma de 1, se representará negada.
Extraer la función en su forma canónica en producto de sumas y suma de productos, de la siguiente tabla:
| A | B | C | S |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
F = A'B'C' + A'BC + AB'C + ABC'

F = (A + B + C')(A + B' + C)(A' + B + C)(A'+B'+C')

En este ejercicio se obtiene una función a partir de una determinada tabla de la verdad. Se obtienen dos funciones distintas, una de suma de productos, obtenida a partir de los unos de las salidas y otra de producto de sumas, obtenidas a partir de los ceros de las salidas.
Simplificar esta expresión mediante la aplicación de los postulados, propiedades y teoremas del álgebra de Boole:
F = (A+B+C)(A+B+D)(A'+B+C')(C+D)(B+D')
__________________________________
__________________________________
F = (A+B+C)(A+B+D)(A'+B+C')(C+D)(B+D')
________________________________
F = A'B'C'+ A'B'D' + A'B'C + C'D' + B'D
_
F = (A'C' + A'D' + A'C + D)B' + C'D'
_
F = A'B + A'B+ CD
_
F = A'B + C'D'
__________
F = A'B + C'D'
F= (A + B')(C+D)

Para simplificar esta función, se ha utilizado el Álgebra de Boole, que se puede definir como las matemáticas de los sistemas digitales. En este sistema, cada variable se designa mediante una letra, y la complementaria de esa variable, se representa con una barra encima de ella (en este caso con una `) Cada función “Booleana” de sumas, multiplicaciones, etc. de variables, es una función lógica, que se puede representar con una puerta. La función básica del Álgebra de Boole es la de representar una función lógica lo mas reducida posible, para que a la hora de implementar el circuito resultante de dicha función, este sea lo más simple y barato posible.
Para lograr estas simplificaciones máximas, el Álgebra de Boole postula una serie de reglas, leyes y postulados para lograrlo.
La primera de estas leyes, es la Ley Conmutativa, que establece que el orden que se aplica a las variables en una operación OR es indiferente.
| A + B = B + A |
La segunda de las leyes es la Ley Asociativa, que establece que al aplicar la operación OR a más de dos variables, el resultado es el mismo, independientemente de la forma en que se agrupen las variables.
| A + (B+C) = (A+B) +C |
La tercera ley es la Ley distributiva, que dice que si se aplica la operación OR a dos o más variables, y luego se aplica la operación AND al resultado de esa operación y otra variable aislada, es equivalente a aplicar la operación AND a la variable aislada con cada uno de las otras dos variables y luego aplicar la operación OR a los productos resultantes.
| A(B + C) = AB+AC |
Además de estas leyes, el Álgebra de Boole tiene una serie de reglas para la simplificación de expresiones booleanas.
| A + 0 = A |
| A + 1 = 1 |
| A · 0 = 0 |
| A· 1 = A |
| A + A = A |
| A + A' = 1 |
| A · A = A |
| A · A' = 0 |
| A · A'' = A |
| A + AB = A + B |
| A + AB = A |
| A + A'B = A+B |
La última parte del Álgebra de Boole, son los Teoremas de DeMorgan, que forman una parte muy importante del Álgebra de Boole, ya que nos indican equivalencias entre distintas puertas.
El primer teorema dice que “ el complemento de dos o más variables a las que se aplica la operación AND es equivalente a aplicar la operación OR a los complementos de cada variable.”
| ___ XY = X' + Y' |
El segundo teorema dice que “ el complemento de dos o más variables a las que se aplica la operación OR es equivalente a aplicar la operación AND a los complementos de cada variable.”
| _____ X + Y = X'Y' |
En el ejercicio realizado, se han utilizado todos los métodos del Álgebra de Boole para la simplificación de la función.
Se comienza aplicando el segundo teorema de DeMorgan para negar dos veces la función. A continuación se utiliza la Ley distributiva para sacar factor común de la función y simplificarla. Y se termina utilizando los postulados para llegar al resultado final.
Transformar las siguientes funciones para poder implementar el circuito exclusivamente con puertas NAND
_____________
F = ABC'D + AB'C
____________
____________
______ _____
F = (abc'd) (ab'c)
______ _____
F = (abc'd) (ab'c)

______ _________
F= (A'+B) (A'+B'+C)
F = (A''B) (A''B''C')
F = (AB') (ABC')

Para la realización de esto ejercicio, se utilizan las Leyes de DeMorgan, incluidas en el Álgebra de Boole.
En el enunciado del ejercicio, indica que las funciones que se presentan, deben ser implementadas en un circuito formado con puertas NAND. Como dichas funciones están escritas con todo tipo de puertas, hay que conseguir convertir esas funciones en multiplicaciones lógicas, para así poder montar el circuito con puertas NAND de dos entradas.
En el primero de los casos, la función viene dada como una suma de productos que se niega a la salida. El primer paso a dar, es convertir esta función en una multiplicación, para lo que se niega dos veces toda la función, obteniéndose dos productos, negados individualmente, y luego negados dos veces a la salida. Si se aplica a toda esta función el postulado 9 del Álgebra de Boole, esta función negada dos veces a la salida, es igual que la misma función sin negar, por lo que se eliminan las negaciones, obteniéndose un producto de productos, que ya si que se puede implementar con puertas NAND.
En el segundo de los casos la función viene presentada como producto de sumas, negados independientemente. Para la conversión de esta función hacemos uso del segundo teorema de DeMorgan, que dice que “el complemento de dos o más variables a las que se aplica la operación OR es equivalente a aplicar la operación AND a los complementos de cada variable.” Según este teorema, las dos sumas que forman la función se podrán convertir en multiplicaciones, negando una vez por separado cada variable de la misma. Como ya existen variables negadas, utilizando de nuevo el postulado 9, desaparecen esas negaciones, con lo que al final se obtiene de nuevo una función de producto de productos para que se pueda implementar con puertas NAND.
7. En la figura siguiente se muestra el dibujo de un sistema de apertura de puerta de un garaje. Para que la puerta se pueda abrir, es necesario, que tanto a la entrada como a la salida el coche se encuentre bien situado sobre la plataforma, para que se activen los pulsadores a1 o b1 y además, que el conductor introduzca una llave en el registro correspondiente (a2 o b2) Si un coche quiere salir y otro quiere entrar al mismo tiempo, la puerta no se abrirá, y una lámpara de color naranja indicará al conductor del coche que desea entrar que se retire para que pueda salir el que está dentro. Otra lámpara del mismo color, que se ilumina al mismo tiempo que la de fuera, indicará al conductor del coche de dentro que debe esperar hasta que se retire el de fuera. Otra lámpara de color rojo, situada al principio del túnel de salida (visible desde las plazas de aparcamiento), indicará al conductor que quiere salir del garaje que modere su velocidad, y espere, por que un coche está situado en la plataforma de entrada.
El coche que quiera entrar o que quiera salir debe permanecer en reposo hasta que la puerta se haya abierto completamente. El cierre de la puerta se produce automáticamente transcurrido un tiempo.
Desarrollar un circuito de control para la apertura de la puerta arrastrada por el motor M y para las señales luminosas LN y LR. Montar el diagrama lógico con puertas NAND de dos entradas y comprobar el funcionamiento.
TABLA DE VERDAD
| A1 | A2 | B1 | B2 | S | LN | LR |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
SM = A'B'CD + A'BCD + ABC'D' + ABC'D
| AB CD | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | |||
| 11 | 1 | 1 | ||
| 10 |
SM = ABC' + A'CD
LN= AB'CD' + AB'CD + ABCD' + ABCD
| AB CD | 00 | 01 | 11 | 10 |
| 00 | ||||
| 01 | ||||
| 11 | 1 | 1 | ||
| 10 | 1 | 1 |
LN = AC
LR = AB'C'D'+AB'C'D+AB'CD' + AB'CD + ABC'D' + ABC'D + ABCD' + ABCD
| AB CD | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | ||
| 01 | 1 | 1 | ||
| 11 | 1 | 1 | ||
| 10 | 1 | 1 |
LR = A

En este ejercicio hay que partir de la base de los puntos que nos indican en el enunciado para construir la tabla de la verdad. Para que el motor funcione tienen que estar como mínimo activados los pulsadores A1 y A2, o B1 y B2 simultáneamente, por lo que estas variables deben tener un valor de 1. En el caso de que los pulsadores A2 o B2 estén activados al mismo tiempo, el sistema considerará que puede abrir la puerta.
Por otro lado existe una luz de advertencia naranja, según la cual si los pulsadores A1 y B1 están activados a la vez, uno de los coches deberá retroceder. También otra luz roja se encenderá cada vez que uno de los pulsadores B1 o A1 esté activado.
Siguiendo estas indicaciones, se obtiene la tabla de verdad, resultando una tabla con cuatro entradas y tres salidas, que indicarán los movimientos de la puerta del garaje así como el encendido o apagado de las luces de indicación.
A partir de la tabla de la verdad, habrá que obtener las funciones lógicas que se correspondan con cada elemento de la salida, es decir, el motor ( S), la luz naranja (LN) y la luz roja (LR) En este caso, al ser menor el número de 1 que de 0 y dado que hay que implementar el circuito con puertas NAND, se ha optado por obtener las funciones lógicas en forma de suma de productos.
Una vez obtenidas las funciones en forma de suma de productos, se procederá a su simplificación. Para ello se va a emplear el Método Gráfico de Karnaugh, que es una técnica mas precisa, y sobre todo más sencilla que la simplificación según el Álgebra de Boole.
Para llevar a cabo el Método Gráfico de Karnaugh es necesario hacer un gráfico que se divide en forma de cuadrícula, tantas como variables tenga la función.
Método de Karnaugh para
funciones de tres variables.
| 00 | 01 | 11 | 10 | |
| 0 | ||||
| 1 |
Las variables de la función están repartidas en dos ejes de coordenadas, y en cada eje deben aparecer todas las posibles combinaciones que se pueden realizar con esas variables. El orden debe ser tal que sólo cambie el valor de una variable, para que exista adyacencia algebraica, y poder agrupar la primera casilla con la última, tanto en sentido vertical como horizontal, simulando un cilindro imaginario.
Una vez que se ha hecho el gráfico, se procede a colocar un 1 o un 0 en cada casilla que cumpla la función. La colocación de un 1 o un 0 dependerá de si la función está expresada en forma de suma de productos o producto de sumas respectivamente. Una vez se haya trasladado la función completa a la tabla, se procederá a agrupar el número de 1 o 0 en función de potencia de 2, es decir, de dos en dos, de cuatro en cuatro, de ocho en ocho, etc., pudiendo además una variable formar parte de mas de un grupo. De cada grupo de 1 ó 0 se obtendrá un término, y se eliminará cada variable que a lo largo o a lo ancho de cada grupo varíen de valor (1,0) Con las variables que no se eliminen y teniendo en cuenta, la forma de la función original, se construirá una nueva función simplificada, para implementarla en el circuito.
En este ejercicio, se pide además de su simplificación, que la función resultante se implemente con puertas NAND de dos entradas, ya que se trata de una “puerta universal”
En primer lugar habría que negar la función dos veces, para poder convertir la función en un producto de productos, eliminando el signo +. Para ello utilizamos el teorema de DeMorgan. Una vez convertida, obtenemos una multiplicación lógica de todos sus valores, negados a la salida de la función, y negados a la salida de cada conjunto de variables de la función, con lo que ya se puede implementar este circuito con puertas NAND, tal y como se puede observar en el gráfico.
Montaje con puertas NAND de dos Entradas

8. Display de 7 Segmentos.
Este ejercicio consiste en montar un display de 7 segmentos partiendo de la base de un codificador 74148 y el display de 7 segmentos. El codificador codificará números digitales, con una relación de 8 a 3. Para realizar la práctica será necesario calcular la tabla de verdad, las funciones, y los esquemas con puertas lógicas que se correspondan con el decodificador 7447, que es un decodificador de BCD a 7 segmentos.
Tabla de Verdad
| A | B | C | A | B | C | D | E | F | G |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Funciones en Producto de Sumas y Simplificaciones por Karnaugh
FA = (A' + B' + C)(A + B' + C')
Esta función no tiene simplificación
FB = (A + B' + C)(A + B + C')
Esta función no tiene simplificación
FC = A' + B + C'
Esta función no tiene simplificación
FD = (A' + B' + C)(A + B' + C')(A + B + C)
Esta función no tiene simplificación
FE = (A' + B' + C)(A' + B +C)(A + B' + C')(A + B' + C)(A + B + C)
| ABC | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 |
FE = (A + B')C
FF = (A' + B' + C)(A' + B + C')(A' + B + C)(A + B + C)
| ABC | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | 0 | |
| 1 | 0 |
FF = (B + C)(A' + C)(A' + B)
FG = (A' + B' + C')(A' + B' + C)(A + B + C)
| ABC | 00 | 01 | 11 | 10 |
| 0 | 0 | 0 | ||
| 1 | 0 |
FG = (A' + B')(A + B + C)
En este ejercicio, se pretende utilizar un display de 7 segmentos, un codificador 74148 y un decodificador 7447. El codificador 74148 es un dispositivo de 8 líneas de entrada y tres de salida, que se emplea para codificar en binario los 8 primeros números del sistema digital. Para utilizar este dispositivo junto con un display de 7 segmentos, es necesario utilizar un decodificador 7447 que decodifica los números binarios, trasladándolos a cada segmento del display. En este caso hipotético, no se dispone del decodificador, por lo que será necesario utilizar puertas lógicas básicas para desempeñar la misma función.
El primer paso es calcular la tabla de verdad. Esta tabla esta formada por tres entradas, que en realidad son las tres salidas del codificador, y por 8 salidas, que son las que se apliquen a cada una de las entradas del display. Hay que tener en cuenta que el codificador 74148 proporciona el valor codificado de las entradas activas en forma negada en la salida, por lo que para calcular la tabla de la verdad, habrá que invertir los términos.
Una vez obtenida la tabla de la verdad, se obtiene la función lógica correspondiente a cada segmento del display. En este caso, y al ser menor el número de 0 que de 1, se obtienen las funciones en forma de producto de sumas. Una vez obtenidas las ocho funciones, correspondientes a cada display, se procede a simplificarlas por el Método de Karnaugh, no pudiéndose simplificar las cuatro primeras de ellas.
Para la representación del circuito se utilizan un codificador 74148, puertas NOT, puertas OR, puertas NAND y un display de 7 segmentos.
El primer paso es conectar mediante interruptores, la fuente de alimentación a cada una de las entradas del codificador, que están numeradas de 0 a 7, siendo estos los números digitales que vamos a convertir en binarios.
Las salidas A0, A1 y A2, serán las que conectemos a nuestro circuito formado con puertas lógicas, para decodificarlas y trasladarlas al display.
El codificador 74148 está compuesto por 8 entradas y por dos terminales EI (Enable Input) y EO (Enable Output) aparte de las entradas Vcc y Gnd.
La entrada Enable Input (EI) es una entrada de habilitación o inhibición que permite codificar el dispositivo cuando se le aplica un nivel bajo. Cuando está en nivel alto, sea cual sea el estado de las entradas, el circuito se inhibe, y no codifica, apareciendo un nivel alto en todas las salidas. En este caso, no se necesita la entrada EI, pero esta si es imprescindible cuando se conectan dos o más codificadores en cascada.
La salida Enable Output (EO) indica mediante un nivel bajo, que ninguna entrada está activada, y que por tanto, está activada la entrada EI con un nivel bajo, pudiendo codificar.
En este caso, ninguno de los dos terminales es necesario para este circuito, ya que nuestras salidas se envían a puertas lógicas para decodificarlas y enviarlas al display.
Si hay que tener en cuenta, que cuando una determinada entrada está activada, con un nivel alto, el dispositivo codifica esta entrada con su número correspondiente, independientemente de cual sea el estado de todas las demás entradas, reconociendo siempre el valor mas alto.
Una vez que se hayan obtenido y simplificado las funciones lógicas, se procederá a implementarlas con puertas lógicas, y una vez implementadas, conectarlas al codificador y al display. Para conectarlas al codificador, se utilizarán sus tres salidas A0, A1, A2, teniendo en cuenta, que A2 se corresponde con el BIT más significante, por lo que se conectarán invertidas las salidas A0 y A2.

8. Codificador 74148
En este ejercicio se va a estudiar el dispositivo 74148, que es un codificador con ocho líneas de entrada y tres de salida, y que tiene como función la de codificar números digitales en números binarios. Éste circuito sólo permite codificar los 8 primeros números binarios, por lo que para conseguir más números, será necesario conectar en cascada varios dispositivos. En el ejercicio se tendrá que construir una tabla de verdad, y responder una serie de preguntas.
| 0' | 1' | 2' | 3' | 4' | 5' | 6' | 7' | 8' | 9' | 10' | 11' | 12' | 13' | 14' | 15' | A3 | A2 | A1 | A0 |
| X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 |
| X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 0 |
| X | X | X | X | X | X | X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| X | X | X | X | X | X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| X | X | X | X | X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| X | X | X | X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| X | X | X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| X | X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| X | X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| X | X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| X | X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| X | X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| X | X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X | X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| X | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
- ¿Cuál es el nivel activo que hay que aplicar a las entradas?
El nivel que hay que aplicar a las entradas es 0, ya que el codificador 74148 niega las entradas a la salida.
- ¿Qué quiere decir que el decodificador es prioritario?
Esto quiere decir que el codificador que el dispositivo va a codificar la entrada mas alta, ignorando todas las que estén a su izquierda, independientemente de su nivel de entrada. Si actuamos sobre la entrada 7, el codificador codificará el número 7 en binario, e ignorará las codificaciones anteriores.
- ¿Qué función cumple la entrada EI?
La entrada EI (Enable Input) es una entada de inhibición que hace que el dispositivo codifique cuando está en un nivel bajo. Si el nivel es alto, sea cual sea el estado de las entradas, el circuito no codifica.
- ¿Qué información suministran las salidas EO y GS?
La salida EO (Enable Output) indica mediante un nivel bajo que ninguna de las entradas está activa, habilitando al dispositivo para codificar. Si alguna de las entradas está activada, EO tendrá un nivel alto.
La salida GS (Group Signal) muestra un nivel bajo cuando alguna entrada está activada, y un nivel alto cuando todas las entradas están inactivas o el circuito inhibido.

El codificador 74148 es un dispositivo con 8 líneas de entrada (0 a 7) y tres de salida (A0, A1 y A2) que convierte números digitales en binario. Para poder codificar números decimales del 0 al 15, son necesarias 16 entradas diferentes, por eso es necesario utilizar dos codificadores diferentes.
El codificador 74148 está compuesto por 8 entradas y por dos terminales EI (Enable Input) y EO (Enable Output) aparte de las entradas Vcc y Gnd. Las salidas que ofrece dicho codificador, aparecen a la salida negadas, por lo que habrá que tenerlo en cuenta a la hora de su utilización.
La entrada Enable Input (EI) es una entrada de habilitación o inhibición que permite codificar el dispositivo cuando se le aplica un nivel bajo. Cuando está en nivel alto, sea cual sea el estado de las entradas, el circuito se inhibe, y no codifica, apareciendo un nivel alto en todas las salidas. Esta es imprescindible cuando, como en este caso, se conectan dos o más codificadores en cascada.
La salida Enable Output (EO) indica mediante un nivel bajo, que ninguna entrada está activada, y que por tanto, está activada la entrada EI con un nivel bajo, pudiendo codificar.
En este caso, al utilizar dos codificadores, será imprescindible utilizar la salida EO de uno de ellos, para completar las cuatro salidas del decodificador.
Las entradas de menor peso (números 0-7) se conectarán al primer codificador para que convierta los números digitales en binario. La salida EO del segundo codificador, se conectará a la entrada EI del primer codificador, para que mientras que no haya un nivel alto en las entradas de este codificador, la salida EO permanezca a nivel bajo, permitiendo al primer dispositivo codificar los números del 0 al 7.
Al estar habilitado el segundo dispositivo, y sin nivel activo en ninguna entrada, todas las salidas presentan nivel alto, por lo que a la salida de todo el dispositivo (puertas NAND) obtendremos de forma negada, el valor de las salidas del primer codificador. Como este tipo de codificadores niega a la salida, obtendremos los ocho primeros dígitos correspondientes al primer codificador. Como la salida EO del segundo codificador presenta un nivel bajo, al no tener activas ninguna de sus entradas, la salida D conectada a una puerta AND, permanecerá con un nivel bajo.
Cuando alguna de las entradas del segundo codificador (8-15) esté en nivel alto, su salida EO estará a nivel alto también, inhibiendo el primer codificador, independientemente de las entradas que tenga. En las salidas A, B y C aparecerá ahora de forma negada la información de las salidas del segundo codificador, que al suministrarlas éste negadas, aparecerán en su forma directa. En este segundo caso, la salida D que es la de mayor peso, aparece a un nivel alto, ya que este es el nivel de la salida EO.
Con este segundo ejercicio, se pretende demostrar la utilidad de la entrada EI y de la salida EO que sirven para habilitar o deshabilitar los codificadores cuando se encuentran conectados dos o más entre sí, y llevarlo a la práctica, probando que cuando el segundo codificador se encuentra habilitado, el primer codificador no codifica y no se tienen en cuenta sus entradas y sus salidas.
Descargar
| Enviado por: | DIMITRI |
| Idioma: | castellano |
| País: | España |
