Ingeniero Industrial
Líneas de transmisión
LÍNEAS DE TRANSMISIÓN.
BIBLIOGRAFÍA.
Líneas de Transmisión. Neri Vela, Rodolfo. McGraw Hill
Cálculo de Antenas. García, A. Alfaomega.
Sistemas de Comunicaciones Electrónicas. Wayne Tomasi, Prentice-Hall.
RESUMEN.-
A diferencia de los ejemplos tratados en el Análisis de Circuitos, en las Líneas de Transmisión (LT) se manejan normalmente tensiones y corrientes con longitudes de onda pequeñas en relación a la longitud total de la línea empleada. Esto implica un tratamiento diferente para las tensiones y corrientes, involucrando una nueva variable que es la posición a lo largo de la línea.
En principio se hará relevante una atenuación de la señal a medida que ésta se propaga a lo largo de la línea y de la misma manera existirá una también una modificación de la fase. Ambos elementos dependerán de las características físicas de la LT y de la frecuencia empleada.
La LT presenta una Impedancia Característica (Z0), y los elementos comentados anteriormente representarán la única complicación si la línea está terminada en una impedancia terminal (ZT) igual a la de la LT. Esta condición define el concepto de línea acoplada.
Para otras condiciones (Z0 distinta de ZT), existirán ondas que se reflejarán desde la carga hacia el generador e interactuarán con las ondas transmitidas. Esto dará lugar a un efecto denominado "onda estacionaria".
Los nuevos elementos para este caso de líneas "desacopladas" son el Coeficiente de Reflexión y la Relación de Onda Estacionaria de Tensión (VSWR = Voltage Standing Wave Ratio).
El objetivo de ingeniería implica conocer los métodos y realizar los cálculos necesarios para lograr que una línea desacoplada se comporte como una línea sin reflexiones, logrando así un uso eficiente de la misma en la transmisión de señales de información o de potencia.
POSTULADOS.-
El estudio de las líneas de transmisión uniformes se basa en el análisis de circuitos con coeficientes distribuidos, por unidad de longitud, el cual se deriva de aplicar las leyes básicas del análisis de circuitos eléctricos a sistemas descritos por los siguientes postulados:
Postulado 1.- El sistema o línea uniforme consiste de dos conductores rectos y paralelos.
El adjetivo "uniforme" significa que los materiales, dimensiones y sección transversal de la línea y el medio que la rodea, permanecen constantes en todo el trayecto. Típicamente en un extremo se conecta una fuente de señal y en el otro una carga, como se muestra:
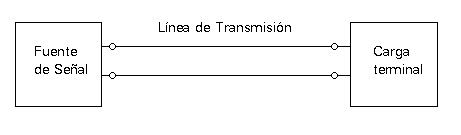
Figura 1.- Representación de una Línea de Transmisión.
No significa que los dos conductores sean del mismo material o tengan la misma forma en su sección transversal. El análisis es válido para un conductor de cualquier material y sección transversal que actúe junto con otro conductor con diferentes características, o para un alambre paralelo a cualquier plano conductor o banda (pista de circuito impreso).
Algunas secciones transversales de conductores usados en ingeniería se muestran:
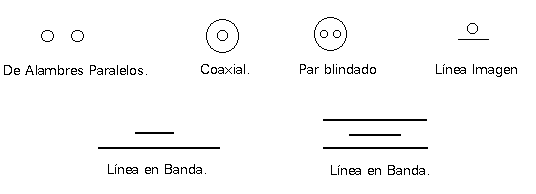
Figura 2.- Secciones transversales de varias líneas de transmisión prácticas.
En general, las torsiones o curvaturas en una línea de transmisión violan el postulado de "uniformidad" y crean efectos no explicables por la teoría de circuito distribuido. Lo mismo sucede con cualquier discontinuidad en la línea, tal como el punto de conexión entre dos líneas uniformes que difieren físicamente en alguna forma.
Postulado 2.- Las corrientes en los conductores de la línea fluyen únicamente en la dirección de la longitud de la línea.
Bajo ciertas condiciones, las señales pueden propagarse en cualquier línea de transmisión uniforme con la totalidad de la corriente o una componente de ella fluyendo alrededor de los conductores, en lugar de fluir a lo largo de ellos. Estos casos no se presentan en una LT y se conocen como modos de propagación en una guía de onda.
Postulado 3.- En la intersección de cualquier plano transversal a los conductores de una línea de transmisión, las corrientes instantáneas totales en los dos conductores son iguales en magnitud, pero fluyen en direcciones opuestas.
En la teoría elemental de redes, para el circuito mostrado en la fig. 1 se estipula que la corriente es la misma en todos los puntos del circuito en un instante dado. El postulado 3 admite que las corrientes instantáneas sean diferentes en distintas secciones transversales de la línea, en el mismo instante.
Claramente esto no es posible sin violar la Ley de Kirchhoff de Corrientes, a menos que éstas puedan fluir transversalmente entre los dos conductores en cualquier parte a lo largo de la longitud de la línea.
Postulado 4.- En la intersección de cualquier plano transversal a los conductores de la línea hay un valor de diferencia de potencial único entre los conductores, en cualquier instante, que es igual a la integral del campo eléctrico a lo largo de todas las trayectorias en el plano transversal, entre cualquier punto sobre la periferia de uno de los conductores y cualquier punto sobre la periferia del otro.
De la misma manera que el postulado 3, este postulado tiene como consecuencia descartar los modos de propagación en la guía de onda, para los cuales la integral del campo eléctrico no es, en general, independiente de la trayectoria.
Postulado 5.- El comportamiento eléctrico de la línea se describe completamente por cuatro coeficientes del circuito eléctrico distribuido, cuyos valores por unidad de longitud de la línea son constantes en cualquier parte de esta. Estos coeficientes de circuito eléctrico son resistencias e inductancias uniformemente distribuidas, como elementos de circuito, en serie a lo largo de la línea, junto con capacitancias y conductancias uniformemente distribuidas, como elementos de circuito, en paralelo a lo largo de la línea.
Es parte esencial de este postulado que los valores de estos coeficientes, a una frecuencia dada, sean determinados únicamente por los materiales y dimensiones de los conductores de la línea y el medio que la rodea. Estos coeficientes no varían ni con el tiempo ni con la tensión o la corriente de la línea.
Las corrientes en la línea están acompañadas de un campo magnético. La inductancia distribuida de la línea es una medida de la energía almacenada en este campo magnético en una unidad de longitud de línea y por unidad de corriente.
Existe pérdida de potencia a medida que las corrientes de línea fluyen por los conductores. La resistencia distribuida de la línea es una medida de la pérdida de potencia en la unidad de longitud de la línea y por unidad de corriente.
La diferencia de potencial de la línea está asociada a un campo eléctrico. La capacitancia distribuida es una medida de la energía almacenada en este campo, en la unidad de longitud de la línea por unidad de diferencia de potencial.
Existe pérdida de potencia en el espacio entre los conductores. La conductancia distribuida de la línea es una medida de esta pérdida, en la unidad de longitud de la línea por unidad de tensión.
La existencia de coeficientes de circuito distribuido en paralelo sugiere la posibilidad de que las corrientes del conductor pueden ser diferentes en distintas secciones transversales de la línea. Corrientes de conducción o corrientes de desplazamiento fluirán entre los conductores en función de la tensión entre ellos o de su tasa de cambio con el tiempo, respectivamente. Las corrientes en la línea en dos secciones transversales separadas, difieren en una cantidad de corriente transversal en la parte de línea tratada.
Definiciones de los Coeficientes.-
Los símbolos para éstos son: R, L, G y C, cuyas definiciones son:
R.- Resistencia total en Serie de la línea por unidad de longitud, incluyendo ambos conductores. Unidades: Ohms/metro.
L.- Inductancia total en Serie de la línea por unidad de longitud, incluyendo la inductancia debida al flujo magnético interno y externo a los conductores de la línea. Henrios/metro.
G.- Conductancia en paralelo de la línea por unidad de longitud. Es una representación de las pérdidas que son proporcionales al cuadrado de la tensión entre los conductores o al cuadrado del campo eléctrico en el medio. Generalmente G representa una pérdida interna molecular de los materiales aislantes dieléctricos. Siemens/metro.
C.- Capacidad en paralelo de la línea por unidad de longitud. Farads/metro.
Nota.- Los símbolos definidos tienen diferentes significados y dimensiones que los empleados en el análisis de circuitos eléctricos. En el caso de las líneas de tx, tratadas como redes de dos puertos con longitudes no despreciables, dichos símbolos representan resistencia, inductancia, etc, por unidad de longitud.
COORDENADAS Y VARIABLES.-
El análisis de la línea de transmisión es unidimensional, con un eje de coordenadas único paralelo a la longitud de la línea. Este es el eje z (minúscula para diferenciar de Z, impedancia.) Dicha coordenada tiene su origen en la fuente de señal.
En algunas ocasiones la distancia de un punto sobre la línea a la carga, se indica por una coordenada d, con origen en la carga y creciendo de derecha a izquierda. El símbolo ð se usa normalmente para la longitud total de la línea. Esto es:
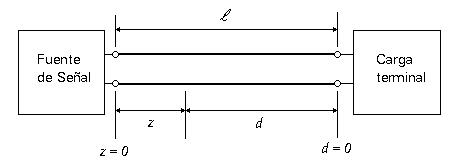
Figura 3.- Coordenadas en una Línea de Transmisión.
Las variables dependientes son la corriente y la tensión, las cuales son funciones del tiempo en cualquier punto de la línea y funciones de su posición en cualquier instante. Así por ejemplo:
i(z, t) = Corriente instantánea en un punto específico sobre la línea de tx, es decir, corriente en el tiempo t y en la coordenada z.
Los símbolos en mayúsculas representan valores fasoriales de números complejos, con magnitudes en valores rms. Si no son designados específicamente como cantidades en la carga o en la fuente de señal, serán funciones de la posición a lo largo de la línea.
I(z) = Valor rms complejo (fasorial) de una corriente, en la coordenada z.
En una coordenada z sobre una línea de tx, como se muestra en la figura siguiente, una tensión se puede representar por una flecha de un conductor a otro, en el plano transversal a z. La punta de la flecha tiene una polaridad positiva, y la tensión es positiva cuando la flecha está dirigida hacia el conductor superior. Similarmente, las corrientes en la coordenada z se indican por dos puntas de flecha una en cada conductor y apuntando en direcciones opuestas (postulado 3). El signo de la corriente es positivo cuando la corriente del conductor superior fluye en la dirección creciente de z.
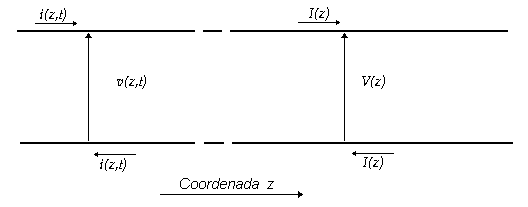
Figura 4.- Tramos de línea de Transmisión mostrando las convenciones especificadas, en el dominio del tiempo y en el de la frecuencia.
CIRCUITO EQUIVALENTE.-
Incorporando los coeficientes de circuito distribuido, una sección de línea se puede representar mediante un circuito equivalente de dos puertos, el cual puede tener distintas configuraciones, una de estas es la sección en L de la figura siguiente, representando una sección infinitesimal de la línea de longitud ð z, localizada en la coordenada z sobre la línea.
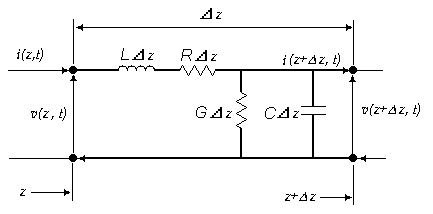
Figura 5.- Circuito equivalente de un elemento infinitesimal de Línea de Transmisión. (Dominio del Tiempo).
ECUACIONES.-
A partir del circuito equivalente, mediante Ley de Kirchhoff de Tensiones:
![]()
--- ( 1 )
Similarmente mediante LKC:
![]()
--- ( 2 )
Dividiendo por ð z y haciendo que ð z tienda a cero, se obtienen las siguientes diferenciales parciales:
![]()
--- ( 3 )
![]()
--- ( 4 )
De estas expresiones se obtiene una ec. diferencial que satisface la onda de tensión:
![]()
--- ( 5 )
y otra expresión similar para la onda de corriente:
![]()
--- ( 6 )
Mediante un proceso similar, pero en función de la frecuencia, se obtienen las siguientes expresiones:
![]()
--- ( 7 )
![]()
--- ( 8 )
Y resolviendo el sistema se obtienen ecuaciones para la tensión y para la corriente:
![]()
--- ( 9 )
![]()
--- ( 10 )
Las ecuaciones diferenciales anteriores determinan las distribuciones de tensión y de corriente a lo largo de la LT. La solución de ellas nos resultan en las ecuaciones siguientes:

--- (11)
![]()
--- (12)
Estas son las ecuaciones generales para la tensión y para la corriente en una línea de transmisión, las cuales se estudiarán en la siguiente parte de estos apuntes.
EJERCICIOS.-
1.- Los coeficientes de circuito distribuido de una línea de transmisión a ð =104 rad/seg son:
R = 0.053 ð /m L = 0.62 ðH/m G = 950 pS/m C = 39.5 pF/m.
En la coordenada z sobre la línea, la corriente instantánea está dada por: i(t) = 75 cos 10 4t mA.
a) Encuentre una expresión para el gradiente de tensión a lo largo de la línea, en el punto z.
b) ¿Cuál es el valor máximo posible del gradiente de tensión?
a) El gradiente de tensión se da en el dominio del tiempo por:

--- (3)
Sustituyendo valores:
= - 0.053 ( 0.075 cos 10 4 t) + ( 0.62 x 10 -6 ) (0.075 x10 4 sen 10 4 t) =
= - 3.98 x10 -3 cos 10 4 t + 0.465 x 10 -3 sen 104 t =
...
= 4.006 x10 -3 cos( 10 4 t - 3.03) Volts/metro.
= 4.006 x10 -3 cos( 10 4 t - 173.4 ð ) Volts/metro.
b) El máximo gradiente de tensión posible es igual a la amplitud de 4 mV. Y sucede cuando:
cos(104 t - 3.03) = 1,
esto implica que:
104 t - 3.03 = 0 , 2ð , 4ð ... radianes.
Esto sucede en los tiempos:
t0 = 3.03 / 104 = 3.03 x 10-4 seg , entonces: t0 = 303 ðS
t1 = (2ð ð 3.03) / 104 = 9.31 x 10-4 seg , ... t1 = 931 ðS
tn = (nð ð 3.03) / 104 n = 0, 2, 4 ...
2.-Para una línea de transmisión con los mismos coeficientes distribuidos, el fasor de tensión en un punto sobre la línea tiene una magnitud rms de 16.5 Volts, y la frecuencia de la señal es de 1100Hz.
Encuentre una expresión para el gradiente del fasor de corriente a lo largo de la línea en el mismo punto.
¿Cuál es la magnitud fasorial rms de la corriente transversal entre los conductores a lo largo de 10 cm de longitud de línea, y cuál es el ángulo de fase con relación a la tensión de la línea en el punto?
¿Cuál es el gradiente máximo de corriente instantánea a lo largo de la línea?
a).- El gradiente de la corriente a lo largo de la línea está dado en el dominio de la frecuencia por:

--- (8)
Solo se deben sustituir valores:
= - [ 950 x 10 -12 + j ( 2ð x 1100 ) ( 39.5x 10 -12 ) ] (16.5 + j 0)
= - ( 0.016 + j 4.51 ) x 10 -6 Amperes/metro
b) La ecuación ð I(z) = -G ðz V(z) - jðC ðz V(z) , (de la cual se deriva la ecuación 8), indica que el cambio en la corriente longitudinal a lo largo de una sección corta de la línea es el negativo de la corriente transversal para la misma sección. Luego la corriente transversal para 10 cm de longitud es de:
Corriente Transversal = 0.1 ( 0.016 + j 4.51 ) x 10-6 Amperes = (0.0016 + j 0.451) x 10-6 = 0.451 x 10-6 ð 1.56
=0.451 x 10-6 ð 89.79ð Amperes.
La corriente transversal adelanta a la tensión por 89.7 grados, ¿En qué elemento de circuito sucede esto?.
c).- Puesto que las magnitudes de todas las cantidades encontradas en los incisos anteriores, expresadas como fasores son valores rms, el gradiente máximo (valor pico) de corriente instantánea a lo largo de la línea es:
Im ð (ððððððð(ððððð ðA/metro
Im = 6.38 ðA/metro
Descargar
| Enviado por: | Alfredo Luna Garcia |
| Idioma: | castellano |
| País: | México |
