Física
Leyes de Newton
Las Leyes de Newton
Las Leyes del Movimiento publicadas en 1687 por Isaac Newton es su obra Principios Matemáticos de la Filosofía Natural describen formalmente los mecanismos del movimiento en general. Estas tres leyes básicas, fundamentadas en observaciones experimentales hace más de tres siglos, constituyen la base de la Mecánica Clásica.
LEY DE LA INERCIA
La primera de la Leyes de Newton explica lo que sucede cuando un cuerpo está ajeno a la interacción con otros cuerpos o cuando la interacción de varios cuerpos hace que el efecto sea nulo. La medida de la interacción con otros cuerpos en lo que conocemos como fuerza. Es por esto que la primera Ley de Newton se puede expresar como: "Si la fuerza externa resultante sobre un determinado cuerpo es cero, entonces su velocidad permanecerá invariante". Es decir, un objeto en reposo permanecerá en reposo y un objeto en movimiento seguirá moviéndose con la misma velocidad (esto es, con la misma rapidez y en línea recta) si es que no actúan sobre él fuerzas externas. Newton expresó esta Ley matemáticamente como:
Si ![]()
F = 0 entonces: a = 0
Lo que sugiere que si la suma total de las interacciones con otros cuerpos es nula, la aceleración del cuerpo será nula, osea que su velocidad seguirá siendo la misma (magnitud, dirección y sentido).
LEY DE LAS FUERZAS
Explica lo que ocurre cuando la fuerza resultante sobre un cuerpo NO es nula. Lo que Newton observó era que mientras que una fuerza esté siendo aplicada a un cuerpo, éste experimentaba un cambio en su velocidad, osea, era acelerado. Newton observó que a medida que aumentaba la magnitud de la fuerza, la aceleración era mayor y por el contrario, cuando disminuía la magnitud de la fuerza, lo mismo ocurría con la aceleración del cuerpo. Ahora, cuando la masa del objeto era mayor, resultaba que la aceleración decrecía un tanto, y por el contrario, cuando la masa era menor, la aceleración aumentaba. De esa manera, Newton elaboró su segunda Ley: "La aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre el e inversamente proporcional a su masa".
![]()
, o en su forma más común: F = m a
Note que esta ley puede llevarnos a la primera. Si hacemos que la fuerza que actúa sobre el cuerpo sea cero, no habrá aceleración, y por lo tanto la velocidad del objeto será invariable, como lo indica la Primera Ley. Es necesario acotar que esta no es la forma en la que Newton expresó exactamente esta Ley, éste lo describió en términos de la tasa de cambio del momento lineal con el tiempo, es decir:
, donde p = m v , es el momento lineal del cuerpo en cuestión.
Esta otra relación también nos lleva a la Primera ley de Newton si hacemos F = 0, ya que en tal caso p sería una constante en el tiempo y por consiguiente también v lo será.
LEY DE LA ACCION - REACCION
Esta ley establece que "si dos cuerpos interactúan, la fuerza ejercida sobre el cuerpo 1 por el cuerpo 2 es igual y opuesta a la ejercida sobre el cuerpo 2 por el cuerpo 1". Lo que es equivalente a decir que las fuerzas siempre ocurren en pares, no puede existir una fuerza individual.
Fuerza de rozamiento
Se debe reconocer que las fuerzas de rozamiento describen la suma de multitud de interacciones elementales de átomos y moléculas situadas en las superficies en contacto.
La fuerza de rozamiento empieza en cero y se incrementa a medida que lo hace la fuerza que se aplica sobre el objeto hasta que se "rompe", y comienza el deslizamiento. Se usa la palabra "rompe" como una analogía con una cuerda que se rompe cuando se incrementa la tensión por encima de un cierto valor crítico.
Los estudiantes tienden, erróneamente, a usar la fórmula Fr=mNcada vez que se presenta una fuerza de rozamiento por deslizamiento.
Se observa que asocian de forma inmediata la reacción del plano con el peso o con la componente del peso en la dirección perpendicular al mismo. Para corregir este defecto, se deberá proponer una situación que contradiga esta suposición, por ejemplo, cuando tiramos de un bloque con una cuerda en una dirección que no sea paralela al plano, véase el apartado fuerza normal.
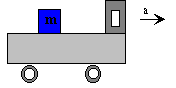
Las fuerzas de rozamiento presentan dificultades a los estudiantes sobre todo en el caso estático, que se pone de manifiesto cuando se estudia la dinámica de una caja sobre la plataforma de un camión que acelera. Se proporciona los datos de la masa y de los coeficientes estático y dinámico de rozamiento, y se le pide calcular la fuerza de rozamiento y la aceleración de la caja cuando se dan tres valores de la aceleración del camión en las siguientes situaciones:
|
| 1. Cuando la caja está en reposo sobre la plataforma. 2. Cuando la caja va a empezar a deslizar sobre la plataforma. 3. Cuando se mueve sobre la plataforma. En este caso, se pide también la aceleración relativa de la caja desde el punto de vista del conductor del camión. |
La principal dificultad del problema radica en poner adecuadamente la fuerza de rozamiento sobre la caja e indicar si tiene o no aceleración, ya que tienden a ponerse en el lugar de los observadores acelerados. Al estar el bloque en reposo sobre la plataforma piensan que su aceleración es nula.
Al plantear el tercer caso, el cálculo de la aceleración de la caja respecto del camión, aceptan que la caja se mueva hacia atrás respecto del camión, sin embargo, les sorprende que se mueva hacia adelante respecto de Tierra.
El estudio de las fuerzas de rozamiento, dedicamos tres páginas web de este capítulo. Se han diseñado dos experimentos simulados, que miden el coeficiente estático de rozamiento y el coeficiente dinámico de rozamiento.
FUERZA ELÁSTICA:
Cuando se aprieta un resorte se puede sentir la llamada fuerza elástica. Algunas bicicletas tienen resortes debajo del asiento para que sea más cómodo conducir
ESFUERZO DE TENSIÓN:
Es la razón de una fuerza aplicada respecto al área sobre la que actúa.
MODULO DE YOUNG:
El esfuerzo es proporcional a la deformación y la constante de proporcionalidad es característica del material.
ESFUERZO / DEFORMACION = CONSTANTE
Si definimos el modulo longitudinal de elasticidad como modulo de young, y podemos escribir la ecuación como:
MODULO DE YOUNG = ESFUERZO LONGITUDINAL / DEFORMACION LONGITUDINAL.
Las unidades del modulo de young son las mismas que las de el esfuerzo, es decir, libras por pulgada cuadrada o pascales. Esto es consecuencia de que la deformación longitudinal es una cantidad sin unidades (dimensional). Algunos valores representativos para alguno de los materiales mas comunes se observan en las tablas:
DINÁMICA DE LAS ROTACIONES (MOMENTOS):
En el caso de la traslación se definió a la Fuerza como la magnitud física que produce variaciones en el
movimiento lineal. La fuerza produce una aceleración, la cual queda definida por la Segunda Ley del
Movimiento: F = m a.
También sabemos que en el caso del movimiento de rotación, la aceleración angular a es la responsable
de las variaciones de la velocidad angular w.
¿ Qué agente externo es el que produce la aceleración angular?.
Consideremos la siguiente situación:
Una partícula P posee una posición dada por su vector posición r , ubicado en el plano xy. Sobre la partícula
actúa una fuerza F con dirección q , contenida también el plano xy. Suponiendo que la distancia de la partícula
al origen permanece constante ( módulo de r es constante), la acción de la fuerza F será el hacer rotar la
partícula en torno al origen del sistema de coordenadas, produciéndole una aceleración angular.
Definamos la magnitud, llamada Momento de la Fuerza o Torque de la fuerza, "t" , al producto vectorial:
t = r x F
El Torque t es un vector cuyo módulo es: t = r F senq. y cuya dirección es perpendicular al plano formado
por los vectores r y F .Es decir, en este caso, en la dirección del eje z., tal como se muestra en la figura anterior.
Nótese que esta dirección queda determinada por el orden del producto vectorial, de modo que según la "regla
del tornillo", al girar r hacia F un tornillo avanzaría en la referida dirección (+ z).
La unidad de medida del Torque es: Ntm , dina cm , libra pié, según el sistema de unidades elegido.
De las condiciones dadas y de la definición del torque se pueden destacar las siguientes propiedades:
1.- De la definición de Torque se concluye que si la partícula se encuentra en el origen del sistema de coordenadas,
o sea, en el "centro de rotación" su torque será nulo, cualquiera sea la fuerza actuante.
2.- Si escribimos el módulo del Torque en la forma: t = (r senq) F , la cantidad entre paréntesis corresponde a la
componente del vector posición en la dirección de la "línea de acción" de la fuerza F. Esta componente r^ se
llama "Brazo de la Fuerza" o "Brazo de Palanca".
De acuerdo a lo anterior, se puede concluir que el Torque de una fuerza se puede calcular como: el producto de
la Fuerza y su "Brazo".
3.- Si escribimos el módulo del Torque en la forma: t = r (F senq) , la cantidad entre paréntesis corresponde
a la componente de la fuerza que es perpendicular al radio de rotación.
F senq = F^ .
4.- Si se invierte uno de los vectores ( r o F ) en el producto vectorial, el resultado es un cambio de signo
en el valor del Torque. Si se invierten ambos vectores, el Torque permanece invariable.
5.- Por convención se ha establecido que los Torques que producen una rotación en la dirección "contraria a
los punteros del reloj", son positivos. Si la rotación es en la dirección opuesta a la anterior, el Torque
es negativo.
Ley de Gravitación Universal
![]()
La fuerza con la que dos cuerpos se atrae, es directamente proporcional al producto de las masas e inversamente proporcional al cuadrado de la distancia que los separa.
Algo similar ocurre con los cuerpos situados en las proximidades de la superficie terrestre:
![]()
Fuerza-peso: Dirección radial, perpendicular a la superficie terrestre. Punto de Aplicación en la masa, sentido hacia el centro de la Tierra.
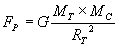
La fuerza con que la Tierra atrae a los cuerpos (Fp) es directamente proporcional al producto de la masa terrestre(Mt) por la masa del cuerpo (Mc) e inversamente proporcional al cuadrado del radio de la tierra (Rt), si el cuerpo se encuentra en las proximidades de la superficie terrestre.
![]()
![]()
Centro de gravedad
LA fuerza más corriente que actúa sobre un cuerpo es su propio peso. En todo cuerpo por irregular que sea, existe un punto tal en el que puedo considerarse en él concentrado todo su peso, este punto es considerado el centro de gravedad .
El centro de gravedad puede ser un punto exterior o interior del cuerpo que se considere.
El conocimiento de la posición de los centros de gravedad, es de suma importancia en la resolución de problemas de equilibrio, porque son los puntos de aplicación de los vectores representativos de los respectivos pesos.
El centro de gravedad de una línea está en el punto de aplicación de un sistema de fuerzas paralelas aplicadas a cada uno de los fragmentos elementales en que se puede considerar descompuesta la misma y proporcionales respectivamente a las longitudes de estos elementos de línea. Si se trata de un elemento rectilíneo, el centro de gravedad se haya en su punto medio. El de un arco de circunferencia puede calcularse mediante recursos de cálculo referencial, y se encuentra situado sobre el radio medio, a una distancia del centro.
En conclusión el centro de gravedad es el punto en el que se encuentran aplicadas las fuerzas gravitatorias de un objeto, o es decir es el pto. en el que actúa el peso. Siempre que la aceleración de la gravedad sea constante, el centro de gravedad se encuentra en el mismo punto que el centro de masas1.
El equilibrio de una partícula o de un cuerpo rígido también se puede describir como estable o inestable en un campo gravitacional. Para los cuerpos rígidos, las categorías del equilibrio se pueden analizar de manera conveniente en términos del centro de gravedad. El Centro de gravedad es el punto en el cual se puede considerar que todo el peso de un cuerpo está concentrado y representado como una partícula. Cuando la aceleración debida a la gravedad sea constante, el centro de gravedad y el centro de masa coinciden.
En forma análoga, el centro de gravedad de un cuerpo extendido, en equilibrio estable, está prácticamente cuenco de energía potencial. Cualquier desplazamiento ligero elevará su centro de gravedad, y una fuerza restauradora lo regresa a la posición de energía potencial mínima. Esta fuerza es, en realidad, una torca que se debe a un componente de la fuerza peso y que tiende a hacer rotar el objeto alrededor de un punto pivote de regreso a su posición original.
Un objeto está en equilibrio estable mientras su Centro de gravedad quede arriba y dentro de su base original de apoyo.
Cuando éste es el caso, siempre habrá una torca de restauración . No obstante cuando el centro de gravedad o el centro de masa cae fuera de la base de apoyo, pasa sobre el cuerpo, debido a una torca gravitacional que lo hace rotar fuera de su posición de equilibrio.
Los cuerpos rígidos con bases amplias y centros de gravedad bajos son, por consiguiente más estables y menos propensos a voltearse. Esta relación es evidente en el diseño de los automóviles de carrera de alta velocidad, que tienen neumáticos y centros de gravedad cercanos al suelo.
Ejemplo:

El centro de gravedad de este auto es muy bajo por lo que es casi imposible que se voltee.
También la posición del centro de gravedad del cuerpo humano tiene efectos sobre ciertas capacidades físicas. Por ejemplo, las mujeres suelen doblarse y tocar los dedos de sus pies o el suelo con las palmas de las manos, con más facilidad que los hombres, quienes con frecuencia se caen al tratar de hacerlo. En general, los hombres tienen el centro de gravedad más alto (hombros más anchos) que las mujeres (pelvis grande), y es por eso que es más fácil que el centro de gravedad de un hombre quede fuera de apoyo cuando se flexiona hacia el frente.
Cuando el centro de gravedad queda fuera de la base de soporte, el objeto es inestable (hay una torsión desplazadora).
En los circos usualmente hay actos de acróbatas y lo que sucede es que el acróbata, cualquiera sea el acto que haga tiene una base de soporte muy angosta, o sea el área pequeña del contacto de su cuerpo con su soporte. Mientras que el centro de gravedad permanezca sobre esta área, él está en equilibrio, pero un movimiento de unos cuantos centímetros sería suficiente para desbalancearlo.
Descargar
| Enviado por: | Borgetti |
| Idioma: | castellano |
| País: | México |