Física
La palanca
TRABAJO PRACTICO DE FISICA APLICADA
Introducción
Maquinaria Simple: son aparatos destinados a equilibrar unas fuerzas con otras y trasladar el pto. de aplicación de unas aplicando ligeramente la intensidad de otras. En toda máquina simple se distinguen dos fuerzas:
(Q) Resistencia, que es la aplicada al cuerpo que se quiere mover
(F) Potencia, que representa la fuerza que debe actuar a fin de equilibrar la resistencia del cuerpo y desplazar su punto de aplicación.
Entre las más importantes citaremos:
-
Palanca
-
Polea
-
Torno
-
Plano Inclinado
-
Cobrestante
-
Cabria
Equilibrio
Equilibrio: se presenta en un cuerpo cuando hay un sistema de fuerzas opuestas e iguales actuando sobre este.
Estas fuerzas son el peso aplicado en el centro de gravedad y la reacción del vínculo aplicado en el punto de suspensión.
Otro dato es que un cuerpo está en equilibrio cuando el centro de gravedad y el punto de suspensión pertenecen a una misma vertical.
Palanca
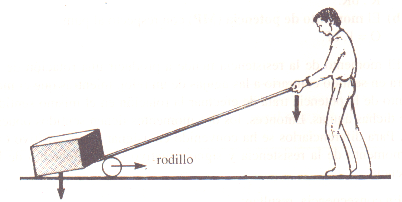
Cuando se desea desplazar un cuerpo pesado, para efectuar menos fuerza, se suele operar así:
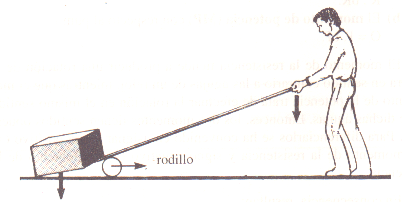
Cuando se desea desplazar un cuerpo pesado, para efectuar menos fuerza, se suele operar así:
Este sistema es un ejemplo de palanca y en él se puede distinguir:
a) una barra rígida que puede girar libremente alrededor de un rodillo. (Punto de apoyo O.)
b) el peso del cuerpo que se quiere mover y que se denomina resistencia(Q).
c) la fuerza que aplica la persona para mover el cuerpo y que se llama
potencia(F).
En consecuencia, podemos establecer que:
Una PALANCA es una barra rígida que puede girar libremente alrededor de un punto de apoyo o de un eje, por la acción de dos fuerzas, la resistencia y la potencia.
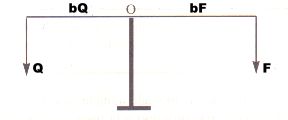
Los elementos de una palanca son:
a) Punto de apoyo (O).
b) Resistencia (Q) = Fuerza que se quiere vencer.
c) Potencia (F) = Fuerza que se aplica.
d) Brazo de resistencia (bQ) = distancia desde el punto de apoyo a la recta de acción de la resistencia.
e) Brazo de potencia (bF) = distancia desde el punto de apoyo a la recta de acción de la potencia.
En una palanca se pueden señalar:
El momento de la resistencia (Mq) con respecto al punto O.
Mo(Q) = Q.bQ
El momento de potencia (Mf) con respecto al punto O
Mo(F) = F . bF.
El momento de la resistencia tiende a producir una rotación de la barra en sentido contrario a las agujas de un reloj, mientras que el momento de la potencia trata de efectuar la rotación en el mismo sentido que dichas agujas.
En consecuencia:
Mq= Q.bQ y Mf= -F.bF
Condición de equilibrio de una PALANCA
Consideremos el siguiente ejemplo de una palanca de 1° género.
bQ bF
bP
Q + P + F -
" Mo(F) = 0
- Mo(F) + Mo(Q) + Mo(P) = 0
- F.bF + Q.bQ + P.bP = 0
F.bF = Q.bQ + PbP
F = Q. bQ + PbP
bF
En forma similar se puede demostrar la condición de equilibrio de la palanca de 2° y 3° género.
Multiplicación de una palanca
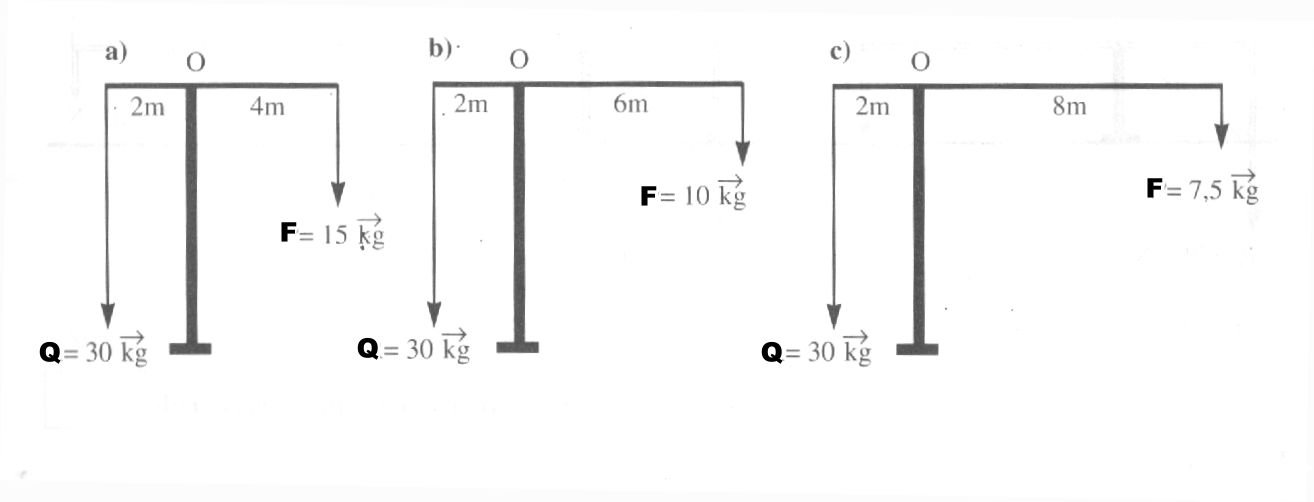
Observemos los siguientes objetos:
En los tres casos se mantiene constante el momento de la resistencia
(Q . bQ) y se incrementa la longitud del brazo de la potencia. Entonces, se reduce el valor de la potencia y, por lo tanto, se debe realizar una fuerza menor para mantener el equilibrio de la palanca.
Asimismo, podemos observar:
bF 4 m
En a) = = 2 y Q = F . 2
bQ 2 m
bF 6 m
En b) = = 3 y Q = F . 3
bQ 2 m
bF 8 m
En c) = = 4 y Q = F . 4
bQ 2 m
bF
Esto demuestra que el cociente da el valor por el cual hay que
bQ
multiplicar la potencia para obtener el valor de la resistencia. A la relación
bF
se la denomina factor de multiplicación.
bQ
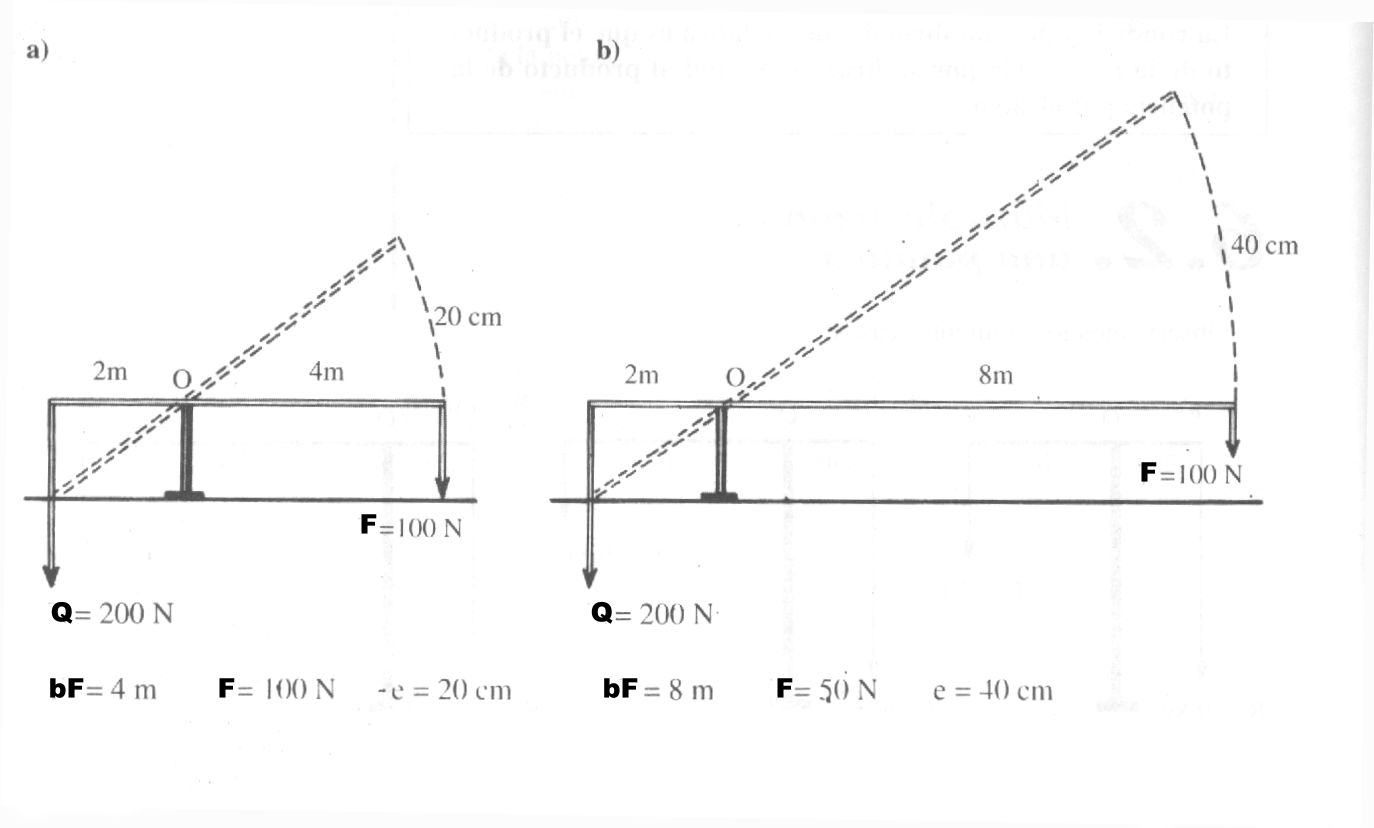
Cuanto mayor es la longitud del brazo de potencia (bF) menor es la fuerza F que se debe aplicar, pero se incrementa el espacio (e) a recorrer:
Lo que se gana es fuerza, se pierde en espacio recorrido
Géneros de palanca
Palanca de primer género:
Una palanca es de primer género cuando el punto de apoyo está ubicado entre la resistencia y la potencia:
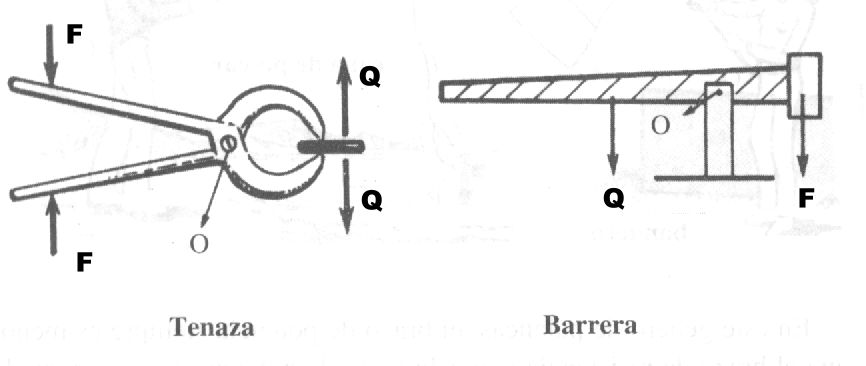
Sabiendo que en el equilibrio de la palanca se cumple:
Q . bQ = F .bF , se deduce:
Cuando el brazo de la potencia es mayor que el brazo de la resistencia (bF > bQ), la potencia es menor que la resistencia
(F < Q) y, en consecuencia, se gana fuerza.
Si bF < bQ resulta F > Q. Se pierde fuerza.
Cuando bF = bQ, es F = Q. No se gana ni se pierde fuerza.
2) Palanca de segundo género:
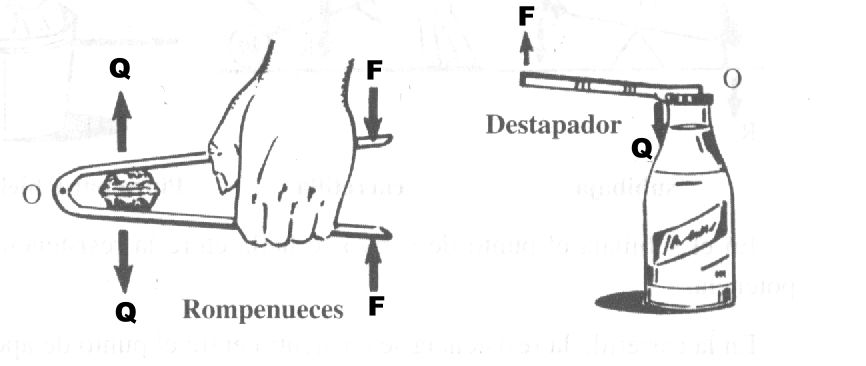
Una palanca es de segundo género cuando la resistencia se halla entre el punto de apoyo y la potencia:
Como en las palancas de segundo género el brazo de potencia es siempre mayor que el brazo de resistencia, en todas ellas se gana fuerza.
Palanca de tercer género:
Cuando la potencia se encuentra entre el punto de apoyo y la resistencia, la palanca es de tercer genero.
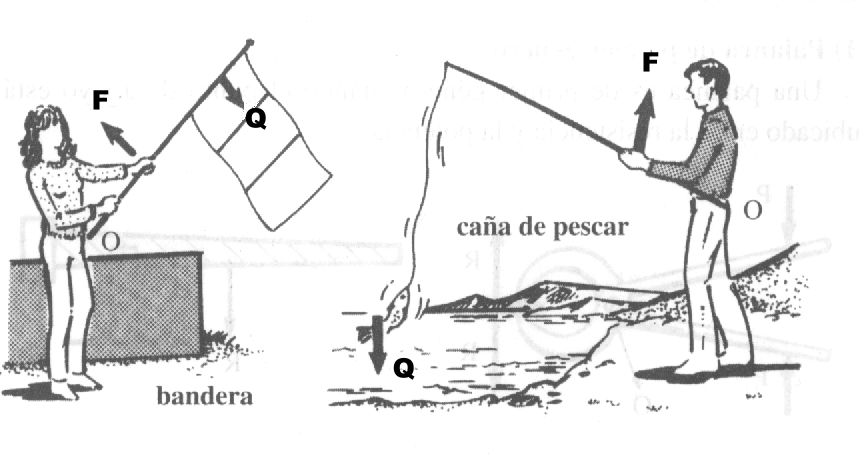
En este género de palancas, el brazo de potencia siempre es menor que el brazo de resistencia y, por lo tanto, la potencia es mayor que la resistencia. Entonces, siempre se pierde fuerza pero se gana comodidad.
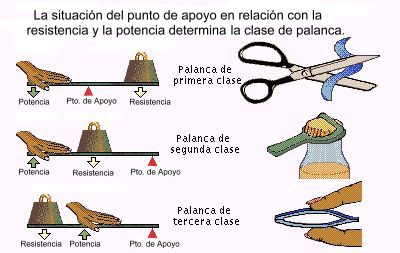
Resumiendo los géneros o clases:
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | España |
