Equipos e instalaciones electrotécnicas
Instalaciones de sonido
Memoria 1
Instalaciones de sonido
Una resistencia.
-
Croquis o esquema
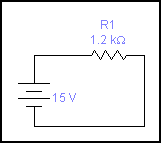
-
Cálculos
R1=1k2 I1= 12,51mA It= 12,51mA Vt=14'8v
-
Cálculos hechos manualmente
It= 12'6mA I1=12'6mA Vt=15v
-
Formulas y operaciones
V = R · I
15 = 1k2 · I
I= 15/1k2
I = 12.5mA
-
Conclusiones
La intesidad es la misma en todo el circuito
Dos resistencias en serie
-
Croquis o esquema
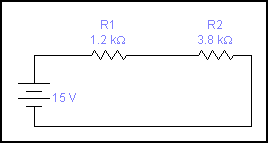
-
Cálculos
Vt= 15v V1= 3,4v V2= 11,1v R1=1k2 R2= 3k8
Rt= 5k I1= 2'8mA I2= 2'9mA It= 2,9mA
-
Formulas y operaciones
V= Rt · It
15= 5k · It Rt= R1 + R2 Vt= V1 + V2
It= 15/5 Rt= 1K2 + 3K8 Vt= 3,4 + 11'1
It= 3Ma Rt= 5k Vt= 15v
-
Conclusiones
Las intensidades en series es siempre la misma.
Para saber el voltaje total en serie se suman los voltajes de cada resistencia
Las resistencias en serie se suman.
Dos resistencias en paralelo.
-
Croquis o esquema
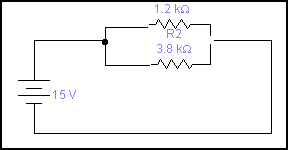
-
Cálculos
Vt=15v R1=1k2 R2= 3k8 Rt= 1
I1= 13mA I2= 3'8 It= 2,5mA
-
Formulas y operaciones
Rt= 1/Rt= 1/R1 + 1/R2 Vt=Rt · I V= R1 · I1
1/Rt= 1/1k2 + 1/3k8 15= 6k5 · I I1= 15/1k8
Rt= 0k912 I= 15/1k I1= 12'6mA
It= 2,3mA
I2= Vt/R2
I2= 15/3k8
I2= 3,9mA
-
Conclusiones
Cuando las resistencias están en paralelo el voltaje siempre es el mismo, y la intesidad total es igual a la suma de las otras intensidades.
Dos resistencias en paralelo y una en serie
-
Croquis o esquema
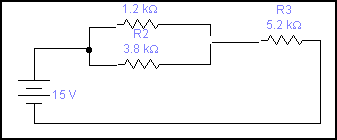
-
Cálculos
Vt=15v V1,2= 14'9v V3= 14'9v
It= 2,2mA I1=3,8mA I2= 12,3mA I3= 5,4mA
Rt= 6k2 R1= 1k2 R2= 3k8 R3=5k2
-
Formulas y operaciones
R(1k2+3k8)= 0,9k It= Vt/Rt I1= 12'6mA
It= 15/6k1 I2= 3,9mA
Rt= R3 + R1,2 It= 2,4mA
Rt= 5k2 + 0k9
Rt= 6k1 I3= 15/5k2
I3= 5k3
-
Conclusiones
En la parte del circuito donde las resistencias están en paralelo el voltaje es el mismo y las intesidades se suman, el resultado de ello, haces que quede 2 resistencias en serie, por lo tanto los voltajes se sumaran y la intesidad será la misma.
Varias combinaciones en serie y paralelo
-
Croquis o esquema
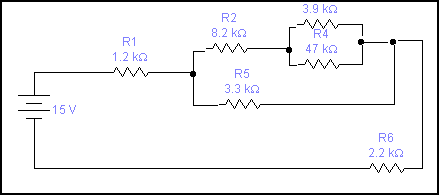
-
Cálculos
R1= 1k2 Vt= 15v I1= 2,3mA
R2= 8k2 V2= 4,32v I2= 0,52mA
R3= 3k9 V3= 2,15v I3= 0,55mA
R4= 47k V4= 2,15v I4= 0,04mA
R5= 3k3 V5= 6,35v I5= 1,92mA
R6= 2k2 V6= 5,35v I6=2,43mA
Rt= 5k97 V1= 2,80v it=2,80mA
-
Formulas y operaciones
R3,4= 1/3'9 + 1/ 47 = 3,36k
R2,+3,4= 3,36 +8,2= 11,56
Rt2, 5= ¡/11'56 + 1/ 3,3 = 2,5k
Rt= R1+ Rt2 + R6= 5k9
I1= 2,80v/1,2= 2,3mA
I2= 4,32v/ 8,2= 0,52mA
I3= 2,15/ 3,9= 0,55mA
I4= 2,15/47= 0,04mA
I5= 6,35/ 3,3= 1,92mA
I6= 5,35/ 2,2= 2,43mA
It= I3+I4 = 0,59
It= It2 =I2= 0,52 It= I2 +I5= 2,4mA It= I1=It3 =I6 = 2,5mA
-
Conclusiones
Para calcular la Rt se empieza por las resistencias que se encuentran en el núcleo del circuito y que están en paralelo, a partir de ahí se va calculando la resta de resistencias, utilizando la función correspondiente según si están en serie o en paralelo.
Para las intensidades se empieza por la primera y se va
Descargar
| Enviado por: | Eduard Martínez |
| Idioma: | castellano |
| País: | España |
