Ingeniero Industrial
Ingeniería económica
UNIDAD 1
LA NATURALEZA BIAMBIENTAL DE LA INGENIERÍA
1.1.- ¿Por qué es tan importante la ingeniería económica?
Porque prácticamente a diario se toman decisiones que afectan el futuro. Las opciones que se tomen cambian la vida de las personas poco y en algunas ocasiones considerablemente. Por ejemplo, la compra en efectivo de una camisa nueva aumenta la selección de ropa del comprador cuando se viste cada día y reduce la suma de dinero que lleva consigo en ese momento. Por otra parte, el comprar un automóvil nuevo y suponer que un préstamo para automóvil nos da opciones nuevas de transporte, puede causar una reducción significativa en el efectivo disponible a medida que se efectúan los pagos mensuales. En ambos casos, los factores económicos y no económicos, lo mismo que los factores tangibles e intangibles son importantes en la decisión de comprar la camisa o el automóvil.
Los individuos, los propietarios de pequeños negocios, los presidentes de grandes corporaciones y los dirigentes de agencias gubernamentales se enfrentan rutinariamente al desafío de tomar decisiones significativas al seleccionar una alternativa sobre otra. Estas son decisiones de cómo invertir en la mejor forma los fondos, o el capital de la Compañía y sus propietarios. El monto del capital siempre es limitado, de la misma manera que en general es limitado el efectivo disponible de un individuo. Estas decisiones de negocios cambiarán invariablemente el futuro, con la esperanza de que sea para mejorar. Por lo normal, los factores considerados pueden ser una vez más, económicos y no económicos, lo mismo tangibles que intangibles.
1.2.- Definición de Ingeniería Económica y su terminología básica
La ingeniería económica hace referencia al la determinación de los factores y criterios económicos utilizados cuando se considera una selección entre una o más alternativas.
Otra definición de ingeniería económica plantea que es una colección de técnicas matemáticas que simplifican las comparaciones económicas. Con estas técnicas es posible desarrollar un enfoque racional y significativo para evaluar los aspectos económicos de los diferentes métodos (alternativas) empleados en el logro del objetivo determinado. Las técnicas pueden funcionar tanto para un individuo como para una corporación que se enfrenta con una decisión de tipo económico.
Los términos comúnmente utilizados en la ingeniería económica son los siguientes:
P = Valor o suma de dinero en un momento denotado como el presente, denominado el valor presente.
F = Valor o suma de dinero en algún tiempo futuro, denominado valor futuro.
A = Serie de sumas de dinero consecutivas, iguales de fin de periodo, denominadas valor equivalente por periodo o valor anual.
n = Número de periodos de interés; años, meses, días.
i = Tasa de interés por periodo de interés; porcentaje anual, porcentaje mensual.
t = Tiempo expresado en periodos; años, meses, días.
UNIDAD 2
2.1 Interés simple e interés compuesto.
Los términos interés, periodo de interés y tasa de interés, son útiles para el cálculo de sumas equivalentes de dinero para un periodo de interés en el pasado y un periodo en el futuro. Sin embargo, para más de un periodo de interés, los términos interés simple e interés compuesto resultan importantes.
El interés simple se calcula utilizando solo el principal, ignorando cualquier interés causado en los periodos de interés anteriores. El interés simple total durante diversos periodos se calcula como:
Interés = (principal) (número de periodos) (tasa de interés)
En donde la tasa de interés está expresada en forma decimal.
Ejemplo: Si se obtiene un préstamo de $1000 para pagar en 3 años a una tasa de interés simple del 5% anual. ¿Cuánto dinero se pagará al final de los tres años?
Interés anual = $1000 * 0.05 = $50
Interés por los tres años = $50 * 3 = $150
Total a pagar al final de los 3 años = $1000 + $150 = $1150
Para el interés compuesto, el interés acumulado para cada periodo de interés se calcula sobre el principal más el monto total del interés acumulado en todos los periodos anteriores. Por lo tanto, el interés compuesto significa un interés sobre el interés, es decir, refleja el efecto del valor del dinero en el tiempo también sobre el interés. El interés compuesto para un periodo de tiempo se calcula:
Interés = (principal + todo el interés causado) (tasa de interés)
Ejemplo: Si se obtiene un préstamo de $1000 al 5% anual compuesto, calcule la suma total a pagar después de los tres años.
Interés año 1 = $1000 * 0.05 = $50
Suma después del año 1 = $1050
Interés año 2 = $1050 * 0.05 = $52.50
Suma después del año 2 = $1102.50
Interés año 3 = $1102.50 * 0.05 = $55.13
Suma después del año 3 = $1157.63
2.2.- Concepto de equivalencia
Cuando se consideran juntos, el valor del dinero en el tiempo y la tasa de interés ayudan a desarrollar el concepto de equivalencia, el cual significa que sumas diferentes de dinero en momentos diferentes son iguales en valor económico. Por ejemplo, si la tasa de interés es de 6% anual, $100 hoy serían equivalentes a $106 en un año a partir de hoy ó $94.34 hace un año. (Ejemplo 1.6 página 14).
2.3 Factores del interés compuesto
Factor de cantidad compuesta pago único (FCCPU) o factor F/P:
F = P (1+i)n
Factor de valor presente, pago único (FVPPU) o factor P/F:
P = F [1 / (1+i)n]
Factor del valor presente, serie uniforme (FVP-SU) o factor P/A:
P = A [(1+i)n-1 / i(1+i)n]
Factor de recuperación del capital (FRC) o factor A/P:
A = P [i(1+i)n / (1+i)n-1]
Factor del fondo de amortización (FA) o factor A/F:
A = F [i / (1+i)n-1]
Factor de cantidad compuesta, serie uniforme (FCCSU) o factor F/A:
F = A [(1+i)n-1 / i]
Notación estándar de los factores:
Para identificar factores es más sencillo utilizar la notación estándar de los nombres de los factores y ésta será utilizada en lo sucesivo:
Nombre del factor notación estándar
| Valor presente, pago único | (P/F,i,n) |
| Cantidad compuesta, pago único | (F/P,i,n) |
| Valor presente, serie uniforme | (P/A,i,n) |
| Recuperación del capital | (A/P,i,n) |
| Fondo de amortización | (A/F,i,n) |
| Cantidad compuesta, serie uniforme | (F/A,i,n) |
La notación anterior es útil para buscar los valores de los factores involucrados los cuales se establecen en las tablas correspondientes, por ejemplo:
(P/A,5%,10) es el factor utilizado en el cálculo de un valor presente, dado el valor de una anualidad, con una tasa de interés del 5% y un valor de 10 periodos de capitalización. Este factor, en las tablas correspondientes es igual a 7.7217
Si utilizamos la fórmula para calcular el valor de este factor (P/A), tenemos:
(P/A,5%,10) = [(1+i)n-1 / i(1+i)n]
= (1.05)10-1 / 0.05(1.05)10
= 7.7217
Ejemplos del la utilización de factores:
Un contratista independiente realizó una auditoria de algunos registros viejos y encontró que el costo de los suministros de oficinas variaban como se muestra en la siguiente tabla:
| Año 0 | $600 |
| Año 1 | $175 |
| Año 2 | $300 |
| Año 3 | $135 |
| Año 4 | $250 |
| Año 5 | $400 |
Si el contratista deseaba conocer el valor equivalente de las 3 sumas más grandes solamente, ¿Cuál será ese total a una tasa de interés del 5%?
F = 600(F/P,5%,10) + 300(F/P,5%,8)+400(F/P,5%,5) F=?
F = $1931.11
0 1 2 3 4 5 6 7 8 9 10
300
400
600
Otra forma de solucionarlo
P = 600+300(P/F,5%,2)+400(P/F,5%,5) = $1185.50
F = $1185.50(F/P,5%,10) = 1185.50(1.6289) = $1931.06
¿Cuánto dinero tendría un hombre en su cuenta de inversión después de 8 años, si depositó $1000 anualmente durante 8 años al 14 % anual empezando en una año a partir de hoy?
F = A(F/A,14%,8) = 1000(13.2328) = $13232.80
¿Cuánto dinero estaría una persona dispuesta a gastar ahora con el fin de evitar el gasto de $500 dentro de 7 años a partir de hoy si la tasa de interés es del 18% anual?
P = F(P/F,18%,7) = 500(0.3139) = $156.95
¿Cuánto dinero estaría una persona dispuesta a pagar ahora por una inversión cuyo retorno garantizado será de $600 anual durante 9 años empezando el año próximo a una tasa de interés del 16% anual?
P = A(P/A,16%,9) = 600(4.6065) = $2763.90
¿Cuánto dinero debo depositar cada año empezando dentro de 1 año al 5.5% anual con el fin de acumular $6000 dentro de 7 años?
A = F(F/A,5.5%,7) = 6000(0.12096) = $725.76 anual.
2.4 Cálculo de tasas de interés desconocidas
En algunos casos, se conoce la cantidad de dinero depositado y la cantidad de dinero recibida luego de un número especificado de años pero de desconoce la tasa de interés o tasa de retorno. Cuando hay involucrados un pago único y un recibo único, una serie uniforme de pagos recibidos, o un gradiente convencional uniforme de pagos recibido, la tasa desconocida puede determinarse para “i” por una solución directa de la ecuación del valor del dinero en el tiempo. Sin embargo, cuando hay pagos no uniformes, o muchos factores, el problema debe resolverse mediante un método de ensayo y error, ó numérico.
Ejemplo: Si Carolina puede hacer una inversión de negocios que requiere de un gasto de $3000 ahora con el fin de recibir $5000 dentro de 5 años, ¿Cuál sería la tasa de retorno sobre la inversión?
P = F [1/(1+i)n]
3000 = 5000 [1 / (1+i)5]
0.600 = 1 / (1+i)5
i = (1/0.6)0.2-1 = 0.1076 = 10.76%
2.5 Cálculo de años desconocidos
En el análisis económico del punto de equilibrio, algunas veces es necesario determinar el número de años (periodos) requerido antes de que la inversión se pague. Otras veces se desea saber cuándo determinadas cantidades de dinero estarán disponibles a partir de una inversión propuesta. En estos casos, el valor desconocido es “n”; para encontrar esta variable pueden utilizarse técnicas similares a aquellas que se utilizan para el cálculo de tasa de interés desconocida.
Ejemplo: ¿Cuánto tiempo tardará duplicar $1000 si la tasa de interés de del 5% anual?
El valor “n” se puede determinar sea mediante el factor F/P o el factor P/F. utilizando el factor P/F.
P = F(P/F,i,n)
1000 = 2000(P/F,5%,n)
(P/F,5%,n) = 0.500
Según la tabla de interés del 5%, el valor 0.5 bajo la columna P/F se encuentra entre 14 y 15 años. Por interpolación, n = 14.2 años.
Por logaritmos: Ln (1.05)n = Ln 2 … n = Ln 2 / Ln 1.05 = 14.21
UNIDAD 3
Tasas nominales y efectivas
Las tasas de interés nominales y efectivas tienen la misma relación que entre sí guardan el interés simple y el compuesto. La diferencia es que las tasas de interés efectivas se utilizan cuando el periodo de capitalización (o periodo de interés) es menor a un año, por ejemplo 1% mensual, deben considerarse los términos de las tasas de interés nominales y efectivas.
El diccionario define la palabra nominal como “pretendida, llamada, ostensible o profesada”. Estos sinónimos implican que una tasa de interés nominal no es una tasa correcta, real, genuina o efectiva.
Las tasas de interés nominales deben convertirse en tasas efectivas con el fin de reflejar, en forma precisa, consideraciones del valor del tiempo. Antes de analizar las tasas efectivas, sin embargo, es preciso definir la tasa de interés nominal, r, como la tasa de interés por periodo por el número de periodos. En forma de ecuación,
R = tasa de interés del periodo * número de periodos.
Puede encontrarse una tasa de interés nominal para cualquier periodo de tiempo mayor que el periodo originalmente establecido. Por ejemplo, una tasa de interés de una periodo que aparece como 1.5% mensual también puede expresarse como un 4.5% nominal por trimestre.
La tasa de interés nominal obviamente ignora el valor del dinero en el tiempo y la frecuencia con la cual se capitaliza el interés. Cuando se considera el valor del dinero en el tiempo al calcular las tasas de interés a partir de las tasas de interés del periodo, la tasa se denomina tasa de interés efectiva. De igual manera que fue válido para las tasas de interés nominales, las tasas efectivas pueden determinarse para cualquier periodo de tiempo mayor que el periodo establecido originalmente.
Para comprender la diferencia entre tasas de interés nominales y efectivas, se determina el valor futuro de $100 dentro de 1 año utilizando ambas tasas. Si un banco paga el 12% de interés compuesto anualmente, el valor futuro de $100 utilizando una tasa de interés del 12% anual es:
F = P(1+i)n = 100(1.12)1 = $112.00
Por otra parte, si el banco paga un interés que es compuesto semestralmente, el valor futuro debe incluir el interés sobre el interés ganado en el primer periodo. Una tasa de interés del 12% anual, compuesto semestralmente significa que el banco pagará 6% de interés después de 6 meses y otro 6% después de 12 meses. Por lo tanto, los valores futuros de $100 después de 6 meses y después de 12 meses son:
F6 = 100(1.06)1 = $106.00
F12 = 106(1.06)1 = $112.36
Donde 6% es la tasa de interés efectiva semestral. En este caso, el interés ganado en 1 año es de $12.36 en vez de $12.00; por consiguiente, la tasa de interés efectiva anual es de 12.36%. la ecuación para determinar la tasa de interés efectiva a partir de la tasa de interés nominal puede generalizarse de la siguiente manera:
i = (1 +r/m)m - 1
donde: i = tasa de interés efectiva por periodo
r = tasa de interés nominal por periodo
m = número de periodos de capitalización
Ejemplo de el cálculo de tasas de interés efectivas:
Una tarjeta de crédito tiene una tasa de interés del 2% mensual sobre el saldo no pagado.
Calcule la tasa efectiva por periodo semestral.
Si la tasa de interés se expresa como 5% por trimestre, encuentre las tasas efectivas por periodos semestrales y anuales.
Solución:
(a) En esta parte del ejemplo, el periodo de capitalización es mensual. Dado que se desea obtener la tasa de interés efectiva por periodo semestral, la “r” debe ser la tasa nominal por 6 meses ó
r = 2% mensual * 6 meses (periodo semestral) = 12% por periodo semestral
la “m” es igual a 6, puesto que el interés estaría compuesto 6 veces en un periodo de 6 meses. Por lo tanto, la tasa efectiva semestral es:
i por cada 6 meses = (1 +0.12/6)6 - 1 = 0.1262 = 12.62%
(b) Para una tasa de interés del 5% por trimestre, el periodo de capitalización es trimestral. Por consiguiente, en un periodo semestral, m = 2 y r = 10%. En consecuencia,
i por cada 6 meses = (1 +10/2)2 - 1 = 0.1025 = 10.25%
La tasa de interés efectiva anual puede determinarse utilizando r = 20% y m = 4, de la siguiente manera:
i por cada año = (1 +20/4)4 - 1 = .02155 = 21.55%
3.2, 3.4 Cálculos para periodos de pago iguales o mayores que los periodos de capitalización
Cuando el periodo de capitalización de una inversión o préstamo no coincide con el periodo de pago, se hace necesario manipular la tasa de interés y/o pago con el fin de determinar la cantidad correcta de dinero acumulado o pagado en diversos momentos. Recuerde que si el pago y los periodos de capitalización no coinciden, no es posible utilizar las tablas de interés hasta hacer las correcciones apropiadas. En esta ocasión analizaremos la situación en la cual el periodo de pago (por ejemplo un año) es igual o mayor que el periodo de capitalización (por ejemplo un mes). Dos condiciones pueden ocurrir:
Los flujos de efectivo requieren del uso de factores de pago único (P/F, F/P).
Los flujos de efectivo requieren el uso de series uniformes o factores de gradientes.
Factores de pago único
En esencia, un número infinito de procedimientos correctos pueden utilizarse cuando solamente hay factores únicos involucrados. Esto se debe a que sólo hay dos requisitos que deben ser satisfechos: (1) Debe utilizarse una tasa efectiva para i. y (2) las unidades en n deben ser las mismas que aquéllas en i. en notación estándar de factores, entonces, las ecuaciones de pago único pueden generalizarse de la siguiente manera:
P = F(P/F, i efectivo por periodo, número de periodos)
F = P(F/P, i efectivo por periodo, número de periodos)
Por consiguiente, para una tasa de interés del 12% anual compuesto mensualmente, podrían utilizarse cualquiera de las i y los valores correspondientes de n que aparecen en la siguiente tabla, en las fórmulas de pago único. Por ejemplo, si se utiliza la tasa efectiva equivalente por mes para i (1%), entonces el término n debe estar en meses (12). Si se utiliza una tasa de interés efectiva semestral para i, es decir (1.03)3 - 1 ó 3.03%, entonces n debe estar en trimestres (4).
| Tasa de interés efectiva | Unidades par n |
| 1% mensual | Meses |
| 3.03% trimestral | trimestres |
| 6.15% semestral | Periodos semestrales |
| 12.68% anual | Años |
| 26.97% cada 2 años | Periodos de 2 años |
El señor Hernández planea invertir su dinero en un depósito que paga el 18% anual compuesto diariamente. ¿Qué tasa efectiva recibirá anual y semestralmente?
i anual = (1+0.18/365)365-1 = 19.72%
i semestral = (1+.09/182)182-1 = 9.41%
Si una persona deposita $1000 ahora, $3000 dentro de 4 años a partir de la fecha del anterior depósito y $1500 dentro de 6 años a una tasa de interés del 12% anual compuesto semestralmente. ¿Cuánto dinero tendrá en su cuenta dentro de 10 años?
Solución: Suponga que se ha decidido utilizar una tasa de interés anual para resolver el problema. Dado que solamente pueden ser utilizadas tasas de interés efectivas en las ecuaciones, el primer paso es encontrar la tasa efectiva anual. De acuerdo con la tabla anterior, para r = 12% y capitalización semestral, i efectivo = 12.36%, o mediante la ecuación:
i anual =(1 +0.12/2)2 - 1 = 0.1236 = 12.36%
Dado que i está expresado en unidades anuales, n debe estar expresado en años. Por lo tanto.
F = 1000(F/P,12.36%,10)+3000(F/P,12.36%,6)+1500(F/P,12.36%,4)
F = 1000(3.21)+3000(2.01)+1500(1.59)
F = $11625.00
Como el interés capitaliza semestralmente, si utilizamos la tasa de interés efectiva semestral, obtenemos el siguiente resultado:
F = 1000(F/P,6%,20)+3000(F/P,6%,12)+1500(F/P,6%,8)
F = 1000(3.2071)+3000(2.0122)+1500(1.5938)
F = $11634.40
Si una mujer deposita $500 cada 6 meses durante 7 años. ¿Cuánto dinero tendrá luego del último depósito si la tasa de interés es del 20% anual compuesto trimestralmente?
n = 14 semestres; convertir la tasa trimestral en semestral
i= (1+0.10/2)2-1 = 10.25% semestral.
F = A(F/A,i,n) = 500(10.25%,14) = 500[(1.1025)14-1/.1025]
F = $14244.53
3.3 Cuando los periodos de pago son menores que los periodos de capitalización
Cuando el periodo de pago es más corto que el periodo de capitalización (PP < PC), el procedimiento para calcular el valor futuro o el valor presente, depende de las condiciones especificadas en relación con la capitalización entre los periodos. La capitalización ínter periódica se refiere al manejo de los pagos efectuados entre los periodos de capitalización. Pueden existir 3 casos posibles:
-
No hay interés pagado sobre el dinero depositado o retirado entre los periodos de capitalización.
-
El dinero depositado o retirado entre los periodos de capitalización gana un interés simple.
-
Todas las transacciones entre los periodos ganan interés compuesto.
En esta ocasión se considera únicamente el caso 1 ya que la mayoría de las transacciones reales del mundo real se encuentran dentro de esta categoría. Si no se paga interés sobre las transacciones entre los periodos, entonces se considera que cualquier cantidad de dinero depositado o retirado entre los periodos de capitalización ha sido depositada al final del periodo de capitalización o retirada al principio de dicho periodo.
Ejemplo: Si la tasa de interés es del 12% anual compuesta trimestralmente, entonces para el siguiente flujo de efectivo, tenemos:
90 120 45
150 200 75 100 50
P = -150 - 200(P/F,3%,1)-85(P/F,3%,2)+165(P/F,3%,3)-50(P/F,3%,4)
P = $317.73
3.5 Tasa de interés efectiva para capitalización continua
A medida que el periodo de capitalización disminuye, el valor m (número de periodos de capitalización) aumenta.
Cuando el interés se capitaliza en forma continua, m se acerca al infinito y la fórmula de tasa de interés efectiva puede escribirse de una nueva forma:
i = er-1
Ejemplo: Para una tasa de interés del 15% anual, la tasa efectiva continua anual es:
i = e0.15-1 = 0.16183 = 16.18%
Para una tasa de interés del 18% anual compuesto en forma continua, calcule la tasa de interés efectiva anual y mensual.
i mensual = e0.18/12-1 = 1.51%
i anual = e0.18-1 = 19.72%
Si un inversionista exige un retorno efectivo de por lo menos el 15% sobre su dinero ¿Cuál es la tasa mínima anual nominal aceptable si tiene lugar una capitalización continua?
0.15 = er-1 --- er = 1.15 --- lner = ln 1.15 --- r = ln 1.15
r = 0.1398 = 13.98%
El señor Rodríguez y la señora Hernández planean invertir $5000 a 10 años a un 10% anual. Calcule el valor futuro para ambos si el señor Rodríguez obtiene un interés compuesto anualmente y la señora Hernández obtiene capitalización continua.
Para el señor R.: F = P(F/P,10%,10) = 5000(2.5937) = $12968.5
Para la señora H.: i = e0.10-1 = 10.52%
F = P(1+i)n = 5000(1.1052)10 = 5000(2.72) = $13594.99
UNIDAD 4
MÉTODO DEL VALOR PRESENTE
4.1.1 Método del valor presente
El método del valor presente de evaluación de alternativas es muy popular debido a que los gastos o los ingresos futuros se transforman en dólares equivalentes de ahora. Es decir, todos los flujos futuros de efectivo asociado con una alternativa se convierten en dólares presentes. En esta forma, es muy fácil, aún para una persona que no está familiarizada con el análisis económico, ver la ventaja económica de una alternativa sobre otra.
La comparación de alternativas con vidas iguales mediante el método del valor presente es directa. Si se utilizan ambas alternativas con capacidades idénticas para el mismo periodo de tiempo, estas reciben el nombre de alternativas de servicio igual.
Con frecuencia, los flujos de efectivo de una alternativa representan solamente desembolsos, es decir, no se estiman entradas. Por ejemplo, se podría estar interesado en identificar el proceso cuyo costo inicial, operacional y de mantenimiento equivalente es más bajo. En otras ocasiones, los flujos de efectivo incluirán entradas y desembolsos. Las entradas, por ejemplo, podrían provenir de las ventas de un producto, de los valores de salvamento de equipo o de ahorros realizables asociados con un aspecto particular de la alternativa. Dado que la mayoría de los problemas que se considerarán involucran tanto entradas como desembolsos, estos últimos se representan como flujos negativos de efectivo y las entradas como positivos.
Por lo tanto, aunque las alternativas comprendan solamente desembolsos, o entradas y desembolsos, se aplican las siguientes guías par seleccionar una alternativa utilizando la medida de valor del valor presente:
Una alternativa: Si VP >= 0, la tasa de retorno solicitada es lograda o excedida y la alternativa es financieramente viable.
Dos alternativas o más: Cuando sólo puede escogerse una alternativa (las alternativas son mutuamente excluyentes), se debe seleccionar aquella con el valor presente que sea mayor en términos numéricos, es decir, menos negativo o más positivo, indicando un VP de costos más bajos o VP más alto de un flujo de efectivo neto de entradas y desembolsos.
En lo sucesivo se utiliza el símbolo VP, en lugar de P, para indicar la cantidad del valor presente de una alternativa.
Ejemplo: Haga una comparación del valor presente de las máquinas de servicio igual para las cuales se muestran los costos a continuación, si la i = 10% anual.
| Tipo A | Tipo B | |
| Costo inicial (P) $ | 2500 | 3500 |
| Costo anual de operación (CAO) $ | 900 | 700 |
| Valor de salvamento (VS) $ | 200 | 350 |
| Vida (años) | 5 | 5 |
La solución queda de la siguiente manera:
VPA = -2500 - 900(P/A,10%,5) + 200(P/F,10%,5) = -$5787.54
VPB = -3500 - 700(P/A,10%,5) + 350(P/F,10%,5) = -$5936.25
Una agente viajera espera comprar un auto usado este año y ha estimado la siguiente información: El costo inicial es $10,000; el valor comercial será de $500 dentro de 4 años; el mantenimiento anual y los costos de seguro son de $1,500; y el ingreso anual adicional debido a la capacidad de viaje es de $5,000. ¿Podrá la agente viajera obtener una tasa de retorno del 20% anual sobre su compra?
Solución: Calcular el VP de la inversión con i = 20%
VP = -10000 + 500(P/F,20%,4) - 1500(P/A,20%,4) + 5000(P/A,20%,4) = -$698.40
No obtendrá una tasa de retorno del 20% porque VP es menor que cero.
4.1.2 Comparación en valor presente de alternativas con vidas diferentes
Cuando se utiliza el método del valor presente para comparar alternativas mutuamente excluyentes que tienen vidas diferentes, se sigue un procedimiento similar al anterior, pero con una excepción: Las alternativas deben compararse durante el mismo número de años. Esto es necesario pues, una comparación comprende el cálculo del valor presente equivalente de todos los flujos de efectivo futuros para cada alternativa. Una comparación justa puede realizarse sólo cuando los valores presentes representan los costos y las entradas asociadas con un servicio igual.
La imposibilidad de comparar un servicio igual siempre favorecerá la alternativa de vida más corta (para costos), aún si ésta no fuera la más económica, ya que hay menos periodos de costos involucrados. El requerimiento de servicio igual puede satisfacerse mediante dos enfoques:
Comparar las alternativas durante un periodo de tiempo igual al mínimo común múltiplo (MCM) de sus vidas.
Comparar las alternativas utilizando un periodo de estudio de longitud de “n” años, que no necesariamente considera las vidas de las alternativas. Este se denomina el enfoque de horizonte de planeación.
Para el enfoque MCM, se logra un servicio igual comparando el mínimo común múltiplo de las vidas entre las alternativas, lo cual hace que automáticamente sus flujos de efectivo extiendan al mismo periodo de tiempo. Es decir, se supone que el flujo de efectivo para un “ciclo” de una alternativa debe duplicarse por el mínimo común múltiplo de los años en términos de dinero de valor constante. Entonces, el servicio se compara durante la misma vida total para cada alternativa. Por ejemplo, si se desean comparar alternativas que tienen vidas de 3 y 2 años, respectivamente, las alternativas son evaluadas durante un periodo de 6 años. Es importante recordar que cuando una alternativa tiene un valor de salvamento terminal positivo o negativo, éste también debe incluirse y aparecer como un ingreso en el diagrama de flujo de efectivo de cada ciclo de vida. Es obvio que un procedimiento como éste requiere que se planteen algunos supuestos sobre las alternativas en sus ciclos de vida posteriores. De manera específica, estos supuestos son:
-
Las alternativas bajo consideración serán requeridas para el mínimo común múltiplo de años o más.
-
Los costos respectivos de las alternativas en todos los ciclos de vida posteriores serán los mismos que en el segundo.
El segundo supuesto es válido cuando se espera que los flujos de efectivo cambien con la tasa de inflación o de deflación exactamente, lo cual es aplicable a través del periodo de tiempo MCM. Si se espera que los flujos de efectivo cambien en alguna otra tasa, entonces debe realizarse un estudio del periodo con base en el análisis de VP. Esta aseveración también se cumple cuando no puede hacerse el supuesto durante el tiempo en que se necesitan las alternativas.
Para el segundo enfoque del periodo de estudio, se selecciona un horizonte de tiempo sobre el cual debe efectuarse el análisis económico y sólo aquellos flujos de efectivo que ocurren durante ese periodo de tiempo son considerados relevantes para el análisis. Los demás flujos de efectivo que ocurran más allá del horizonte estipulado, bien sea que ingresen o que salgan, son ignorados. Debe hacerse y utilizarse un valor de salvamento realista estimado al final del periodo de estudio de ambas alternativas. El horizonte de tiempo seleccionado podría ser relativamente corto, en especial cuando las metas de negocios de corto plazo son muy importantes, o viceversa. En cualquier caso, una vez que se ha seleccionado el horizonte y se han estimado los flujos de efectivo para cada alternativa, se determinan los valores VP y se escoge el más económico. El concepto de periodo de estudio u horizonte de planeación, es de particular utilidad en el análisis de reposición.
Ejemplo: Un administrador de planta está tratando de decidir entre dos máquinas excavadoras con base en las estimaciones que se presentan a continuación:
| Máquina A | Máquina B | |
| Costo inicial P | 11000 | 18000 |
| Costo anual de operación | 3500 | 3100 |
| Valor de salvamento | 1000 | 2000 |
| Vida (años) | 6 | 9 |
Determinar cuál debe ser seleccionada con base en una comparación de valor presente utilizando una tasa de interés del 15% anual.
Si se especifica un periodo de estudio de 5 años y no se espera que los valores de salvamento cambien, ¿Cuál alternativa debe seleccionarse?
¿Cuál máquina debe ser seleccionada en un horizonte de 6 años si se estima que el valor de salvamento de la máquina B es de $6000 después de 6 años?
Solución:
Puesto que las máquinas tienen vidas diferentes, estas deben compararse con su MCM, que es 18 años. Para ciclos de vida posteriores al primero, el primer costo se repite en el año 0 del nuevo ciclo, que es el último año del ciclo anterior. Estos son los años 6 y 12 para la máquina A y al año 9 para la máquina B.
VPA = -11000-11000(P/F,15%,6)-11000(P/F,15%,12)-3500(P/A,15%,18) +1000(P/F,15%,6)+1000(P/F,15%,12)+1000(P/F,15%,18) = -$38599.20
VPB = -18000-18000(P/F,15%,9) - 3100(P/A,15%,18) + 2000(P/F,15%,9) + 2000((P/F,15%,18) = $41384.00
Se selecciona la máquina A puesto que cuesta menos en términos de VP que la máquina B.
Para un horizonte de planeación a 5 años no se necesitan repeticiones de ciclo y VSA = $1000 y VSB = $2000 en el año 5. El análisis VP es:
VPA = -11000 - 3500(P/A,15%,5) + 1000(P/F,15%,5) = -$22235.50
VPB = -18000 - 3100(P/A,15%,5) + 2000(P/F,15%,5) = -$27397.42
La máquina A sigue siendo la mejor selección.
Para el horizonte de planeación de 6 años, VSB = $6000 en el año 6.
VPA = -11000 - 3500(P/A,15%,6) + 1000(P/F,15%,6) = -$23813.45
VPB = -18000 - 3100(P/A,15%,6) + 6000(P/F,15%,6) = -$27138.15
Definitivamente la máquina A es la mejor alternativa.
La firma ASVERA Cementos planea abrir una nueva cantera. Se han diseñado dos planes para el movimiento de la materia prima desde la cantera hasta la planta. El plan A requiere la compra de dos volquetas y la construcción de una plataforma de descargue en la planta. El plan B requiere la construcción de un sistema de banda transportadora desde la cantera hasta la planta. Los costos para cada plan se detallan más adelante en la tabla correspondiente.
Mediante el análisis del VP, determinar cuál plan debe seleccionarse si el dinero vale actualmente 15% anual.
| Plan | A | Plan B | |
| volqueta | plataforma | Banda transportadora | |
| Costo inicial | 45000 | 28000 | 175000 |
| Costo anual de operación | 6000 | 300 | 2500 |
| Valor de salvamento | 5000 | 2000 | 10000 |
| Vida (años) | 8 | 12 | 24 |
Solución: La evaluación debe incluir del MCM de 8 y 12, es decir, 24 años. La reinversión en las 2 volquetas ocurrirá en los años 8 y 16, y la plataforma nuevamente deberá ser comprada en el año 12. No se necesita reinversión para el plan B.
Para simplificar los cálculos, analicemos que los CAO de el plan A son $9800 más elevados que para el plan B (2 volquetas = (12000 + 300) - 2500 = 9800
Por lo tanto, el VPA = VP volquetas + VP plataforma + VPCAO
VP volquetas = -90000 - 90000(0.3269) - 90000(0.1069) +10000(0.3269) + 10000(0.1069) + 10000(0.0349) = -$124355.00
VP plataforma = -28000 - 28000(0.1869) + 2000(0.1869) + 2000(0.0349 = -$32789.60
VPCAO = -9800(6.4338) = -$63051.24
Por lo tanto el VP plan A = -$220195.84
Para el plan B se resuelve de la siguiente manera:
VP plan B = -175000 + 10000(0.0349) = -$174651.00
Como se puede apreciar, el plan más viable es el plan B (es el menos negativo), por lo que se debe optar por esta alternativa y construir la banda transportadora.
Ejemplo: Un propietario de un restaurante está tratando de decidir entre dos vaciadores de desechos de basura. Un vaciador de acero común (AC) tiene un costo inicial de $65000 y una vida de 4 años. La otra alternativa es un vaciador resistente al óxido construido principalmente de acero inoxidable (AI), cuyo costo inicial es de $110000; se espera que éste dure 10 años. Debido a que el vaciador AI tiene un motor ligeramente más grande, se espera que su operación cueste alrededor de $5000 más por año que la del vaciador AC. Si la tasa de interés es 16% anual, ¿Cuál alternativa debe seleccionarse?
AC: P = $65000; n = 4 años; A = $0.00
AI: P = $110000; n = 10 años; A = $5000
VP (AC) = -65000 - 65000(P/F,16%,4) - 65000(P/F,16%,8) - 65000(P/F,16%,12) - 65000(P/F,16%,16) = -$137,722.00
VP (AI) = -110000 - 110000(P/F,16%,10) - 5000(P/A,16%,20) = -$164,581.00
Debe adquirir el vaciador de acero común, ya que es el que presenta el menor valor presente total.
4.1.3 Cálculos del costo capitalizado
El costo capitalizado (CC) se refiere al valor presente de un proyecto cuya vida útil se supone durará para siempre. Algunos proyectos de obras públicas tales como diques, sistemas de irrigación y ferrocarriles se encuentran en esta categoría. Además, las dotaciones permanentes de universidades o de organizaciones de caridad se evalúan utilizando métodos de costo capitalizado. En general, el procedimiento seguido al calcular el costo capitalizado de una secuencia infinita de flujos de efectivo es el siguiente:
Trace un diagrama de flujo de efectivo que muestre todos los costos y/o ingresos no recurrentes (una vez) y por lo menos dos ciclos de todos los costos y entradas recurrentes (periódicas).
Encuentre el valor presente de todas las cantidades no recurrentes.
Encuentre el valor anual uniforme equivalente (VA) durante un ciclo de vida de todas las cantidades recurrentes y agregue esto a todas las demás cantidades uniformes que ocurren en los años 1 hasta el infinito, lo cual genera un valor anual uniforme equivalente total (VA).
Divida el VA obtenido en el paso 3 mediante la tasa de interés “i” para lograr el costo capitalizado.
Agregue el valor obtenido en el paso 2 al valor obtenido en el paso 4.
El propósito de empezar la solución trazando un diagrama de flujo de efectivo debe ser evidente. Sin embargo, el diagrama de flujo de efectivo es probablemente más importante en los cálculos de costo capitalizado que en cualquier otra parte, porque éste facilita la diferenciación entre las cantidades no recurrentes y las recurrentes o periódicas.
Costo capitalizado = VA / i ó VP = VA / i ; P = A / i
Ejemplo: Calcule el costo capitalizado de un proyecto que tiene un costo inicial de $150,000 y un costo de inversión adicional de $50,000 después de 10 años. El costo anual de operación será de $5,000 durante los primeros 4 años y $8,000 de allí en adelante. Además se espera que haya un costo de adaptación considerable de tipo recurrente por $15000 cada 13 años. Suponga que i = 15 % anual.
P1 = -150,000 - 50,000(P/F,15%,10[0.2472]) = -$162,360.00
A1 = -15,000(A/F,15%,13[0.02911] = -$436.65
P2 = -436.65 / 0.15 = -$2911.00
P3 = 5,000 / 0.15 = -$33,333.33
P4 = -3,000 / 0.15 (P/F,15%,4[0.5718]) = -$11,436.00
VP = P1 + P2 + P3 + P4 = -$210,040.33
Actualmente hay dos lugares en consideración para la construcción de un puente que cruce el río Ohio. El lado norte, que conecta una autopista estatal principal haciendo una ruta circular interestatal alrededor de la ciudad, aliviaría en gran medida el tráfico local. Entre las desventajas de éste lugar se menciona que el puente haría poco para aliviar la congestión de tráfico local durante las horas de congestión y tendría que ser alargado de una colina a otra para cubrir la parte más ancha del río, las líneas del ferrocarril y las autopistas locales que hay debajo. Por consiguiente, tendría que ser un puente de suspensión. El lado sur requeriría un espacio mucho más corto, permitiendo la construcción de un puente de celosía, pero exigiría la construcción de una nueva carretera.
El puente de suspensión tendría un costo inicial de $30,000,000 con costos anuales de inspección y mantenimiento de $15,000. Además, el suelo de concreto tendría que ser repavimentado cada 10 años a un costo de $50,000. Se espera que el puente de celosía y las carreteras cuesten $12,000,000 y tengan costos anuales de mantenimiento de $10,000. Así mismo, éste tendría que ser pulido cada 10 años a un costo de $45,000. Se espera que el costo de adquirir los derechos de vía sean de $800,000 para el puente de suspensión y de $10,300,000 para el puente de celosía. Compare las alternativas con base en su costo capitalizado si la tasa de interés es de 6% anual.
Solución:
Alternativa 1: P = 30,000,000 + 800,000; A = 15,000; R1 = 50,000 c/10 años.
Alternativa 2: P = 12,000,000 + 10,300,000; A = 8,000; R1 = 10,000 c/ 3 años; R2 =45,000 c/ 10 años.
VP1 = -30,000,000 - 800,000 -(15,000/0.06) - ((50,000/0.06)(A/F,6%,10)[0.07587]) = -$31,113,225.00
VP2 = -12,000,000 - 10,300,000 -- ((10,000/0.06(A/F,6%,3)[0.31411]) - ((45,000/0.06(A/F,6%,10)[0.07587]) = -$22,542,587.50
Se debe construir el puente de celosía, puesto que su costo capitalizado es más bajo.
Ejemplo: Un ingeniero de una ciudad está considerando dos alternativas para el suministro de agua local. La primera alternativa comprende la construcción de un embalse de tierra sobre un río cercano, que tiene un caudal altamente variable. El embalse formará una represa, de manera que la ciudad pueda tener una fuente de agua de la cual pueda depender. Se espera que el costo inicial del embalse sea de $8,000,000 con costos de mantenimiento anual de $25,000 y que el embalse dure indefinidamente.
Como alternativa, la ciudad puede perforar pozos en la medida requerida y construir acueductos para transportar el agua a la ciudad. El ingeniero estima que se requerirá inicialmente un promedio 10 pozos a un costo de $45,000 por cada uno, incluyendo la tubería de conducción. Se espera que la vida promedio de un pozo sea de 5 años con un costo anual de operación de $12,000 por pozo. Si la tasa de interés que se utiliza es del 15% anual, determine cuál alternativa debe seleccionarse con base en sus costos capitalizados.
Alternativa 1: P = 8,000,000; A = 25,000
Alternativa 2: P = 45,000 * 10; n = 10 años; A = 12,000 * 10
VP1 = -8,000,000 - 25,000/0.15 = -$8,166,666.67
A1 = -45,000*10(A/P,15%5[0.29832]) = -134,244.00
A2 = 12,000 * 10 = 120,000
VP2 = (A1 + A2)/i = (-134,244 - 120,000) / 0.15 = -$1,694,960.00
Los costos son considerablemente más baratos que el embalse.
4.2 Método del valor anual uniforme equivalente
El método VA se utiliza comúnmente para comparar alternativas. El VA significa que todos los ingresos y desembolsos son convertidos en una cantidad anual uniforme equivalente de fin de periodo, que es la misma cada periodo.
La ventaja principal de éste método sobre todos los demás radica en que en este no se requiere hacer comparación sobre el mínimo común múltiplo de los años cuando las alternativas tienen vidas útiles diferentes, es decir, el VA de la alternativa se calcula para un ciclo de vida únicamente, porque como su nombre lo implica, el VA es un valor anual equivalente sobre la vida del proyecto. Si el proyecto continúa durante más de un ciclo, se supone que el valor anual equivalente durante el siguiente ciclo y todos los ciclos posteriores es exactamente igual que para el primero, siempre y cuando todos los flujos de efectivo actuales sean los mismos para cada ciclo.
La condición repetible de la serie anual uniforme a través de diversos ciclos de vida puede demostrarse con el siguiente ejemplo.
El valor anual para dos ciclos de vida de un activo con un costo inicial de $20,000, un costo de operación anual de $8,000 una vida de 3 años y una i=22%.
El VA para un ciclo de vida se calculará de la siguiente manera:
VA = -20,000(A/P,22%,3[0.48966])-8000 = -$17793.20
El VA para dos ciclos de vida:
VA = -20,000(A/P,22%,6[0.31576])-20,000(P/F,22%,3[0.5507])(A/P,22%,6)-8000 = -$17793.20
4.2.1 y 4.2.4 Período de estudio para alternativas con vidas útiles diferentes
El método de valor anual para comparar alternativas es probablemente el más simple a realizar. La alternativa seleccionada tiene el costo equivalente más bajo o el ingreso equivalente más alto.
Tal vez la regla más importante de recordar al hacer las comparaciones VA es la que plantea que sólo debe de considerarse un ciclo de vida de cada alternativa, lo cual se debe a que el VA será el mismo para cualquier número de ciclos de vida que para uno.
Ejemplo: Los siguientes datos han sido estimados para dos máquinas de pelar tomates que prestan el mismo servicio, las cuales serán evaluadas por un gerente de una planta enlatadora:
| Máquina A | Máquina B | |
| Costo inicial | 26,000 | 36,000 |
| Costo de mtto. Anual | 800 | 300 |
| Costo de mano de obra anual | 11,000 | 7,000 |
| ISR anuales | - | 2,600 |
| Valor de salvamento | 2,000 | 3,000 |
| Vida en años | 6 | 10 |
Si la tasa de retorno mínima requerida es 15% anual, ¿Cuál máquina debe seleccionar el gerente?
VAA = -26,000(A/P,15%,6[0.26424]+2000(A/F,15%,6[0.11424]) - 11800
= -$18,441.76
VAB = -36000(A/P,15%,10[0.19925])+3000(A/F,15%10[0.04925]) -9900
= -$16,925.25
Se selecciona la máquina B puesto que representa el costo anual más bajo.
Suponga que la Compañía del ejemplo anterior está planeando salir del negocio de enlatados de tomates dentro de 4 años. Para ese momento, la compañía espera vender la máquina A en $12,000 o la máquina B en $15,000. Se espera que todos los demás costos continúen iguales. ¿Cuál máquina debe comprar la compañía bajo estas condiciones?
Si todos los costos, incluyendo los valores de salvamento, son los mismos que se habían estimado originalmente, ¿Cuál máquina debe seleccionarse utilizando un horizonte de 4 años?
VAA = -26000(A/P,15%,4[0.35027]) +12000(A/F,15%,4[0.20027]) -11800 = -$18,503.78
VAB = -36000(A/P,15%,4[0.35027]) + 15000(A/F,15%,4[0.20027]) -9900 = -$19,505.67
Se selecciona la máquina A.
VAA = -26000(A/P,15%,4[0.35027]) + 2000(A/F,15%,4[0.20027])-11800 = -$20,506.48
VAB = -36000(A/P,15%,4[0.35027]) + 3000(A/F,15%,4[0.20027]) - 9900 = -$21,908.91
Se selecciona la máquina A.
4.2.2 Método de fondo de amortización de salvamento
Cuando un activo tiene un valor de salvamento terminal (VS), hay muchas formas de calcular el VA.
En el método del fondo de amortización de salvamento, el costo inicial P se convierte primero en una cantidad anual uniforme equivalente utilizando el factor A/P. Dado normalmente, su carácter de flujo de efectivo positivo, después de su conversión a una cantidad uniforme equivalente a través del factor A/F, el valor de salvamento se agrega al equivalente anual del costo inicial. Estos cálculos pueden estar representados por la ecuación general:
VA = -P(A/P,i,n) + VS(A/F,i,n) ; naturalmente, si la alternativa tiene cualquier otro flujo de efectivo, éste debe ser incluido en el cálculo completo de VA.
Ejemplo: Calcule el VA de un aditamento de tractor que tiene un costo inicial de $8000 y un valor de salvamento de $500 después de 8 años. Se estima que los costos anuales de operación de la máquina son $900 y se aplica una tasa de interés del 20% anual.
VA = -8000(AP,20,8[0.26061]) + 500(AF,20,,8[0.06061]) - 900 = -2954.58
Ejemplo: una pizzería local acaba de comprar una flota de cinco mini vehículos eléctricos para hacer entregas en un área urbana. El costo inicial fue de $4600 por vehículo y su vida esperada y valores de salvamento son 5 años y $300 respectivamente. Se espera que los costos combinados del seguro, mantenimiento, recargo y lubricación sean de $650 el primer año y aumenten en $50 anuales de ahí en adelante. El servicio de entrega generará una cantidad extra estimada de $1200 anuales. Si se requiere un retorno del 10% anual, use el método del VA para determinar si la compra debió haberse hecho.
VA = 5*4600(AP,10,5[0.2638]) + 5*300(AF,10,5[0.1638])-650 - 50(AG,10,5[1.8101] + 1200 = -$5362.21
Puesto que VA es menor < 0 y se espera un retorno del 10%, la compra no se justifica.
4.2.3 Método del valor presente de salvamento
El método del valor presente también convierte las inversiones y valores de salvamento en un VA. El valor presente de salvamento se retira del costo de inversión inicial y la diferencia resultante es anualizada con el factor A/P durante la vida del activo.
La ecuación general es: VA = -P + VS(P/F,i,n)(A/P,i,n).
Los pasos para obtener el VA del activo completo son:
Calcular el valor presente del valor de salvamento mediante el factor P/F.
Combinar el valor obtenido en el paso 1 con el costo de inversión P.
Anualizar la diferencia resultante durante la vida del activo utilizando el factor A/P.
Combinar cualquier valor anual uniforme con el paso 3.
Convertir cualquier otro flujo de efectivo en un valor anual uniforme equivalente y combinar con el valor obtenido en el paso 4.
Ejemplo: Calcule el VA del aditamento de tractor del ejemplo anteriormente analizado utilizando el método del valor presente de salvamento.
VA = [-8000 + 500(PF,20,8[0.2326])](AP,20,8[0.26061]) - 900] = -$2,954.57
4.2.5 Costo anual uniforme equivalente de una inversión perpetua
La evaluación de proyectos de control de inundaciones, canales de irrigación, puentes u otros proyectos de gran escala, requiere la comparación de alternativas cuyas vidas son tan largas que pueden ser consideradas infinitas en términos de análisis económico. Para este tipo de análisis es importante reconocer que el valor anual de la inversión inicial es igual simplemente al interés anual ganado sobre la inversión global, como lo expresa la siguiente ecuación: A = Pi.
Los flujos de efectivo que son recurrentes en intervalos regulares o irregulares se manejan exactamente igual que en los cálculos VA convencionales, es decir, son convertidos a cantidades anuales uniformes equivalentes durante un ciclo, lo cual de manera automática las anualiza para cada ciclo de vida posterior.
El sistema operador de aguas del estado de Puebla está considerando dos propuestas para aumentar la capacidad del canal principal en su sistema de irrigación en la localidad de valle bajo.
La propuesta A comprendería el dragado del canal con el fin de retirar el sedimento y la maleza acumulados durante su funcionamiento en años anteriores. Dado que la capacidad del canal tendrá que mantenerse en el futuro cerca del caudal, debido a la mayor demanda de agua, la oficina está planeando comprar equipo y accesorios de dragado por $65,000. Se espera que el equipo tenga una vida de 10 años y un valor de salvamento de $7,000. Se estima que los costos anuales de mano de obra y de operación para el funcionamiento del dragado totalizan $22,000. Para controlar la formación de maleza en el canal mismo y a lo largo de los bancos se aplicará herbicidas durante la época de irrigación. Se espera que el costo anual del programa de control de maleza sea de $12,000.
La propuesta B involucraría el revestimiento del canal con el concreto a un costo inicial de $650,000. Se supone que el revestimiento es permanente, pero será necesario efectuar algún mantenimiento cada año por un costo de $1,000. Además, tendrán que hacerse reparaciones de revestimiento cada 5 años a un costo de $10,000. Compare las dos alternativas con base en el valor anual uniforme equivalente utilizando una tasa de interés del 5% anual.
| A | B |
| P = -$65,000 | P = -$650,000 |
| n = 10 años | A = -$1,000 |
| VS = $7,000 | F = $10,000 (cada 5 años) |
| A1 = -$22,000 | |
| A2 = -$12,000 |
VAA = -65000(AP,5,10[0.1295] + 7000(AF,5,10[0.07950]) - 22000 - 12000 = -$41,861.00
VAB = -650,000(0.05) - 1000 - 10,000(AF,5,5[0.18097]) = -$35,309.70
Debe seleccionarse la alternativa B puesto que representa el menor valor anual uniforme equivalente.
Ejemplo: Si el joven Vera deposita ahora una tasa de interés del 7% anual, ¿Cuántos años debe acumularse el dinero antes de que pueda retirar $1,400 anuales por tiempo indefinido?
VPn = VA/i = 1400/0.07 = 20,000 es el valor presente necesario.
¿En cuanto tiempo los $10,000 iniciales serán $20,000?
F = P(F/P,7%,n) ----- 20000= 10000(1.07)n
n = ln 2 / ln 1.07
n = 10.24 años.
Unidad 5
5.1 Conceptos generales sobre el cálculo de la tasa de retorno
Si el dinero se obtiene en préstamo, la tasa de interés se aplica al saldo no pagado de manera que la cantidad y el interés total del préstamo se pagan en su totalidad con el último pago del préstamo. Desde la perspectiva del prestamista o inversionista, cuando el dinero se presta o se invierte, hay un saldo no recuperado en cada periodo de tiempo. La tasa de interés es el retorno sobre éste saldo no recuperado, de manera que la cantidad total y el interés se recuperan en forma exacta con el último pago o entrada. La tasa de retorno define estas dos situaciones.
Tasa de retorno (TR) es la tasa de interés pagada sobre el saldo no pagado de dinero obtenido en préstamo, o la tasa de interés ganada sobre el saldo no recuperado de una inversión, de manera que el pago o entrada final iguala exactamente a cero el saldo con el interés considerado.
La tasa de retorno está expresada como un porcentaje por periodo, por ejemplo, i = 10% anual. Ésta se expresa como un porcentaje positivo; es decir, no se considera el hecho de que el interés pagado en un préstamo sea en realidad una tasa de retorno negativa desde la perspectiva del prestamista. El valor numérico de “i” puede moverse en un rango entre -100% hasta el infinito.
La definición anterior no establece que la tasa de retorno sea sobre la cantidad inicial de la inversión, sino más bien sobre el saldo no recuperado, el cual varía con el tiempo. El siguiente ejemplo demuestra la diferencia entre estos dos conceptos:
Ejemplo: Para i = 10% anual, se espera que una inversión de $1000 produzca un flujo de efectivo neto de $315.47 para cada 4 años.
A = 1000(AP,10,4[0.3155]) = $315.47
Esto representa una tasa de retorno del 10% sobre el saldo no recuperado. Calcule la cantidad de la inversión no recuperada para cada uno de los 4 años utilizando (a) la tasa de retorno sobre el saldo no recuperado y (b) la tasa de retorno sobre la inversión inicial de $1000.
a)
| Año | Saldo inicial no recuperad | Interés sobre saldo no rec. | Flujo de efectivo | Cantidad recuperada | Saldo final no recuperad |
| 0 | - | - | 1000 | - | 1000 |
| 1 | 1000 | 100 | 315.47 | 215.47 | 784.53 |
| 2 | 784.53 | 78.45 | 315.47 | 237.02 | 547.51 |
| 3 | 547.51 | 54.75 | 315.47 | 260.72 | 286.79 |
| 4 | 286.79 | 28.68 | 315.47 | 286.79 | 0 |
261.88 1000
b)
| Año | Saldo inicial no recuperad | Interés sobre saldo no rec. | Flujo de efectivo | Cantidad recuperada | Saldo final no recuperad |
| 0 | - | - | 1000 | - | 1000 |
| 1 | 1000 | 100 | 315.47 | 215.47 | 784.53 |
| 2 | 784.53 | 100 | 315.47 | 215.47 | 569.06 |
| 3 | 569.06 | 100 | 315.47 | 215.47 | 353.59 |
| 4 | 353.59 | 100 | 315.47 | 215.47 | 138.12 |
400 861.88
Para determinar la tasa de retorno i de los flujos de efectivo de un proyecto, se debe definir la relación TR. El valor presente de las inversiones o desembolsos, VPD se iguala al valor presente de los ingresos VPR. En forma equivalente, los dos pueden restarse e igualarse a cero, es decir:
VPD = VPR
0 = -VPD + VPR
El enfoque de valor anual utiliza los valores VA en la misma forma para resolver para i.
VAD = VAR
0 = -VAD + VAR
El valor que hace estas ecuaciones numéricamente correctas es la raíz de la relación TR. Se hace referencia a este valor i mediante otros términos adicionales a la tasa de retorno: tasa interna de retorno (TIR), tasa de retorno de equilibrio, índice de rentabilidad y retorno sobre la inversión (RSI). Éstos se representan por la notación i*.
5.2 Cálculo de la tasa de retorno por el método del valor presente
Para entender con mayor claridad los cálculos de la tasa de retorno, recuerde que la base para los cálculos de la Ingeniería Económica es la equivalencia, o el valor del dinero en el tiempo. En los cálculos de la tasa de retorno, el objetivo es encontrar la tasa de interés i* a la cual la cantidad presente y la cantidad futura con equivalentes.
La columna vertebral del método de la tasa de retorno es la relación TR. Por ejemplo, si alguien deposita $1000 ahora y le prometen un pago de $500 dentro de 3 años y otro de $1500 en 5 años a partir de ahora, la relación de la tasa de retorno utilizando VP es:
1000 = 500(PF,i*,3) + 1500(PF,i*,5)
Despejando tenemos:
0 = -1000 + 500(PF,i*,3) + 1500(PF,i*,5)
La ecuación se resuelve para “i*” y se obtiene i* = 16.9%
i* utilizando ensayo y error manual: El procedimiento general empleado para calcular una tasa de retorno utilizando la ecuación de valor presente y cálculos manuales de ensayo y error es el siguiente:
Trazar un diagrama de flujo de efectivo.
Plantear la ecuación de la tasa de retorno.
Seleccionar valores de i mediante ensayo y error hasta que la ecuación esté equilibrada.
Al utilizar el método de ensayo y error para determinar i*, es conveniente acercarse bastante a la respuesta correcta en el primer ensayo. Si los flujos de efectivo se combinan, de tal manera que el ingreso y los desembolsos pueden estar representados por un solo factor tal como P/F o P/A, es posible buscar en tablas la tasa de interés correspondiente al valor de ese factor para “n” años. El problema es entonces el combinar los flujos de efectivo en el formato de uno solo de los factores estándar, lo cual puede hacerse mediante el siguiente procedimiento:
Convertir todos los desembolsos en cantidades bien sean únicas (P ó F) o cantidades uniformes (A), al ignorarse el valor del dinero en el tiempo. Por ejemplo, si se desea convertir un valor anual en un valor futuro, multiplique simplemente por A el número de años. El esquema seleccionado para el movimiento de los flujos de efectivo debe ser aquel que minimiza el error causado por ignorar el valor del dinero en el tiempo. Es decir, si la mayoría de los flujos de efectivo son una A y una pequeña cantidad es F, la F se debe convertir en A en lugar de hacerlo al revés y viceversa.
Convertir todas las entradas en valores bien sea únicos o uniformes.
Después de haber combinado los desembolsos y las entradas, de manera que se aplique bien sea el formato P/F, P/A, o A/F, se deben utilizar las tablas de interés aproximada al cual se satisface el valor P/F, P/A, o A/F, respectivamente, para el valor apropiado de n. La tasa obtenida es una buena cifra aproximada para utilizar en el primer ensayo.
Es importante reconocer que la tasa de retorno obtenida en esta forma es solamente una estimación de la tasa de retorno real, ya que ignora el valor del dinero en el tiempo. El procedimiento se ilustra en el ejemplo siguiente:
Ejemplo: Si se invierten $5000 ahora en acciones comunes, los cuales se espera que produzcan $100 anualmente durante 10 años y $7000 al final de esos 10 años, ¿Cuál es la tasa de retorno?
0 = -5000 + 100(PA,i*,10) + 7000(P/F,i*,10)
Utilice el procedimiento de estimación de la tasa de interés a fin de determinar la i para el primer ensayo. Todo el ingreso será considerado como una sola F en el año 10, de manera que pueda utilizarse el factor P/F.
El factor P/F ha sido seleccionado porque la mayoría del flujo de efectivo (es decir $7000) ya encaja en este factor y los errores creados por ignorar el valor del dinero en el tiempo restante serán minimizados. Solamente para la primera estimación es i, defina P = 5000, n = 10 y F = (10*100) + 7000 = 8000.
Ahora puede plantearse que 5000 = 8000(P/F,i,10)
(P/F,i,10) = 0.625
La i aproximada está entre 4% y 5%. Por consiguiente, se debe utilizar i = 5% para estimar la tasa de retorno real.
0 = -5000 + 100(P/A,5,10[7.7217]) + 7000(P/F,5,10[0.6139]) = 69.47
0< 69.47
Este cálculo es aún muy alto por el lado positivo, lo que indica que el retorno es más del 5%. Ensaye i = 6%
0 = -5000 + 100(PA,6,10[7.3601]) + 7000(P/F,6,10[0.5584]) = -355.19
0> -355.19
Dado que la tasa de interés del 6% es muy alta, interpole entre el 5% y el 6% para obtener:
i* = 5.16%
5.3 Cálculo de la tasa de retorno por el método del CAUE
De la misma manera como i* puede encontrarse utilizando una ecuación VP, también puede determinarse mediante la forma VA. Este método se prefiere, por ejemplo, cuando hay flujos de efectivo anuales uniformes involucrados. El procedimiento es el siguiente:
Dibuje un diagrama de flujo de efectivo.
Defina las relaciones para el VA de los desembolsos, VAD y entradas VAR con i* como variable desconocida.
Defina la relación de la tasa de retorno en la forma de la ecuación 0 = VAD + VAR.
Seleccione valores de i por ensayo y error hasta que la ecuación esté equilibrada. De ser necesario, interpole para encontrar i*.
Ejemplo: Utilice cálculos de VA a fin de encontrar la tasa de retorno para los flujos de efectivo del ejemplo anterior.
Las relaciones VA para desembolsos y entradas son:
VAD = -5000(AP,i,10) y VAR = 100 + 7000(AF,i,10)
0 = -5000(AP,i*,10) + 100 + 7000(AF,i*,10)
La solución de ensayo y error produce los resultados:
En i = 5%, 0< 9.02
En i = 6%,0> -48.26
Por interpolación se obtiene i* = 5.16%
5.4 Interpretación de la tasa de retorno sobre la inversión adicional
Como ya se planteó, el primer paso al calcular la TR sobre la inversión adicional es la preparación de una tabla que incluye valores incrementales del flujo de efectivo. El valor en esta columna refleja la inversión adicional requerida que debe ser presupuestada si se selecciona la alternativa con el costo inicial más alto, lo cual es importante en un análisis TR a fin de determinar una TIR de los fondos adicionales gastados por la alternativa de inversión más grande. Si los flujos de efectivo incrementales de la inversión más grande no la justifican se debe seleccionar la alternativa más barata. Pero, ¿Qué decisión tomar sobre la cantidad de inversión común a ambas alternativas? ¿Se justifica ésta de manera automática?, básicamente sí, puesto que debe seleccionarse una de las alternativas mutuamente excluyentes. De no ser así, debe considerarse la alternativa de no hacer nada como una de las alternativas seleccionables, y luego la evaluación tiene lugar entre 3 alternativas.
5.5 Evaluación de la tasa de retorno incremental utilizando el método del valor presente
El procedimiento completo para análisis TR aplicado a dos alternativas que comprenden solamente flujos de efectivo negativo es:
Ordene las alternativas por tamaño de la inversión empezando con la más baja. La alternativa con la inversión inicial más alta está en al columna B
Desarrolle el flujo de efectivo y las series incrementales del flujo de efectivo utilizando el MCM de años, suponiendo la reinversión en alternativas, según sea necesario.
Dibuje un diagrama de flujo de efectivo incremental (Si lo cree necesario)
Cuente el número de cambios de signo en la serie de flujo de efectivo incremental para determinar si hay tasas de retorno múltiples presentes.
Establezca la ecuación VP para los flujos de efectivo incrementales y determine el retorno i*B-A utilizando ensayo y error manual, o ingresando los valores del flujo de efectivo incremental del paso 2 en un sistema de hoja de cálculo para determinar i*B-A.
Si i*B-A < TMAR, seleccione la alternativa A. Si i*B-A >TMAR, se justifica la inversión adicional; seleccione la alternativa B
Ejemplo: Un fabricante de ropa de cuero está considerando la compra de una máquina de coser industrial nueva, la cual puede ser semiautomática o completamente automática. Las estimaciones son:
| Semiautomática | Totalmente automática | |
| Costo inicial | 8000 | 13000 |
| Desembolsos anuales | 3500 | 1600 |
| Valor de salvamento | 0 | 2000 |
| Vida, años | 10 | 5 |
Determine cuál máquina debe seleccionarse si la TMAR es 15% anual.
Solución
Utilice el procedimiento antes descrito para estimar i*
La alternativa A es la semiautomática (s) y la alternativa B es la máquina totalmente automática (t).
Los flujos de efectivo deben de realizarse para el MCM, es decir, 10 años y se representan en la siguiente tabla:
| (1) | (2) | (3) = (2) - (1) | |
| Año | Flujo de efectivo (s) | Flujo de efectivo (t) | F. de efec. Incremen. |
| 0 | -8000 | -13000 | -5000 |
| 1 al 5 | -3500 | -1600 | +1900 |
| 5 | -- | +2000 -13000 | -11000 |
| 6 al 10 | -3500 | -1600 +2000 | +1900 +2000 |
| Total | -43000 | -38000 | +5000 |
El diagrama de flujo de efectivo incremental se mostrará mas adelante.
En la serie del flujo de efectivo incremental hay 3 cambios de signo que indican hasta 3 raíces. En la serie incremental acumulada, que empieza negativamente en S0 = -5000 y continúa hasta S10 = +5000, también hay 3 cambios de signo indicando que no existe una raíz positiva.
La ecuación de tasa de retorno basada en el VP de los flujos de efectivo incremental es:
0 = -5000 + 1900(P/A,i,10) - 11000(P/F,i,10) + 2000(P/F,i,10)
Si es razonable suponer que la tasa de reinversión es igual a un valor i* resultante, se generará una TRC de i´ = i*. La solución de la ecuación anterior para la primera raíz descubierta producirá una i*t-s entre 12 y 15%. Mediante interpolación i*t-s = 12.72
Puesto que la tasa de retorno de 12.72% sobre la inversión adicional es menor que la TMAR del 15%, debe comprarse la semiautomática de menor costo.
La tasa de retorno determinada hasta ahora puede interpretarse en realidad como valores de equilibrio, es decir, una tasa a la cual puede seleccionarse cualquier alternativa. Si el flujo de efectivo incremental i* es mayor que la TMAR, se elige la alternativa de inversión más grande.
5.6 Selección de alternativas mutuamente excluyentes utilizando el análisis de la tasa de retorno.
Como en cualquier alternativa de selección de ingeniería económica, hay diversas técnicas se solución correctas. Los métodos VP y VA analizados anteriormente son los más directos. Estos métodos utilizan TMAR especificada a fin de calcular el VP o VA para cada alternativa. Se selecciona la alternativa que tiene la medida más favorable de valor. Sin embargo, muchos gerentes desean conocer la TR para cada alternativa cuando se presentan los resultados. Éste método es muy popular en primer lugar debido principalmente al gran atractivo que tiene conocer los valores TR, aunque en ocasiones se aplica en forma incorrecta. Es esencial entender la forma de realizar a cabalidad un análisis TR basado en los flujos de efectivo incrementales entre alternativas para asegurar una selección de alternativas correcta.
Cuando se aplica el método TR, la totalidad de la inversión debe rendir por lo menos la tasa mínima atractiva de retorno. Cuando los retornos sobre diversas alternativas igualan o exceden la TMAR, por lo menos uno de ellos estará justificado ya que su TR > TMAR. Éste es el que requiere la menor inversión. Para todos los demás, la inversión incremental debe justificarse por separado. Si el retorno sobre la inversión adicional iguala o excede la TMAR, entonces debe hacerse la inversión adicional con el fin de maximizar el rendimiento total del dinero disponible.
Por lo tanto, para el análisis TR de alternativas múltiples, se utilizan los siguientes criterios.
Seleccionar una alternativa que:
Exija la inversión más grande.
Indique que se justifica la inversión adicional frente a otra alternativa aceptable.
Una regla importante de recordar el evaluar alternativas múltiples mediante el método TR es que una alternativa nunca debe compararse con aquella para la cual no se justifica la inversión incremental. El procedimiento TR es:
Ordene las alternativas aumentando la inversión inicial, es decir, de la más baja a la más alta.
Determine la naturaleza de la serie de flujos de efectivo: algunos positivos o todos negativos.
Algunos flujos de efectivo positivos, es decir, ingresos. Considera la alternativa de no hacer nada como el defensor y calcule los flujos de efectivo entre la alternativa de no hacer nada y la alternativa de inversión inicial más baja (el retador). Vaya al paso 3.
Todos los flujos de efectivo son negativos, es decir, solamente costos. Considere la alternativa de inversión inicial más baja como el defensor y la inversión siguiente más alta como el retador. Salte al paso 4.
Establezca la relación TR y determine i* para el defensor. (Al comparar contra la alternativa de no hacer nada, la TR es, en realidad, el retorno global para el retador). Si i* < TMAR, retire la alternativa de inversión más baja de mayor consideración y calcule la TR global para la alternativa de inversión siguiente más alta. Después repita este paso hasta que i* >= TMAR para una de las alternativas; entonces ésta alternativa se convierte en el defensor y la siguiente alternativa de inversión más alta recibe el nombre de retador.
Determine el flujo de efectivo incremental anual entre el retador y el defensor utilizando la relación:
Flujo de efectivo incremental = flujo de efectivo retador - flujo de efectivo defensor.
Calcule la i* para la serie de flujos de efectivo incremental utilizando una ecuación basada en el VP o en el VA (el VP se utiliza con mayor frecuencia).
Si i* >= TMAR, el retador se convierte en el defensor y el defensor anterior deja de ser considerado. Por el contrario, si i* < TMAR, el retador deja de ser considerado y el defensor permanece como defensor contra el próximo retador.
Repita los pasos 4 a 6 hasta que solamente quede una alternativa. Ésta es seleccionada.
Ejemplo: Se han sugerido cuatro ubicaciones diferentes para una construcción prefabricada, de las cuales sólo una será seleccionada. La información de costos y el flujo de efectivo neto anual se detallan más adelante en la tabla correspondiente. La serie de flujo de efectivo neto anual varía debido a diferencias en mantenimiento, costos de mano de obra, cargos de transporte, etc. Si la TMAR es del 10%, se debe utilizar el análisis TR para seleccionar la mejor ubicación desde el punto de vista económico.
| Estimaciones para cuatro ubicaciones posibles de construcción | ||||
| Ubicación | A | B | C | D |
| Costo de construcción $ | -200000 | -275000 | -190000 | -350000 |
| Flujo de efectivo anual $ | +22000 | +35000 | +19500 | +42000 |
| Vida, años | 30 | 30 | 30 | 30 |
Solución: Todas las alternativas tienen vida de 30 años y los flujos de efectivo anuales incluyen ingresos y desembolsos.
El procedimiento antes esquematizado produce el siguiente análisis:
En la siguiente tabla, primera línea, las alternativas se ordenan por costo de construcción creciente:
| Cálculo de la tasa de retorno para cuatro alternativas | ||||
| Ubicación | C | A | B | D |
| Costo de construcción | -190000 | -200000 | -275000 | -350000 |
| Flujo de efectivo anual | +19500 | +22000 | +35000 | +42000 |
| Proyectos comparados | C no hacer nada | A no hacer nada | B frente a A | D frente a B |
| Costo incremental | -190000 | -200000 | -75000 | -75000 |
| Flujo de caja incremental | +19500 | +22000 | +13000 | +7000 |
| (P/A,i*,30) | 9.7436 | 9.0909 | 5.7692 | 10.7143 |
| I* (%) | 9.63 | 10.49 | 17.28 | 8.55 |
| ¿Se justifica el incremento? | No | Sí | Sí | No |
| Proyecto seleccionado | No hacer | A | B | C |
Se presentan algunos flujos de efectivo positivos; utilice el paso 2, parte (a) para comparar la ubicación C con la alternativa de no hacer nada (identificada como no hacer)
La relación TR es:
0 = -190000 + 19500(PA,i*,30)
La columna 1 de la tabla anterior presenta el valor del factor calculado (PA,i*,30) de 9.7436 y de i* = 9.63%. Puesto que 9.63% <10%, se elimina la ubicación C. Ahora la comparación es A de no hacer nada y la columna 2 muestra que i*A = 10.49%, lo cual elimina la alternativa de no hacer nada; el defensor es ahora A y el retador es B.
La serie del flujo de efectivo incremental, columna 3 e i* para una comparación B a A se determina a partir de:
0 = -275000 - (-200000) + (35000 - 22000)(PA,i*,30)
= -75000 + 13000(PA,i*,30)
De acuerdo con las tablas de interés, de debe buscar el factor P/A en la TMAR, que es (P/A,10%,30) = 9.4269. Ahora, cualquier valor P/A de la ecuación anterior mayor que 9.4269 indica que i* será inferior al 10% y por consiguiente, es inaceptable. El factor P/A de la ecuación del punto 4 es 5.7692. Para fines de referencia, i* = 17.28%.
La alternativa B se justifica incrementalmente y será el nuevo defensor, eliminando así la alternativa A.
Al comparar D con B (pasos 4 y 5) se genera la relación VP, 0 = -75000 + 7000(PA,i*,30) y un valor PA de 10.7143 (i*D-B = 8.55%). Con ello se elimina la ubicación D y sólo permanece la alternativa B, la cual es la seleccionada.
Ejemplo: De cuatro máquinas diferentes que se utilizarán en operaciones de limpieza de agua marina, sólo una debe comprarse. Seleccione una máquina que utilice la TMAR del presidente de la compañía del 13.5% anual y las estimaciones de la siguiente tabla:
| Costos para cuatro alternativas de máquinas | ||||
| Máquina | 1 | 2 | 3 | 4 |
| Costo inicial | -5000 | -6500 | -10000 | -15000 |
| CAO | -3500 | -3200 | -3000 | -1400 |
| V. S. | +500 | +900 | +700 | +1000 |
| Vida, años | 8 | 8 | 8 | 8 |
Solución: Las máquinas ya están ordenadas de acuerdo con un costo inicial creciente; no hay ingresos involucrados y las estimaciones de vida son todas iguales. Se realizan comparaciones incrementales directamente para las dos alternativas. Esto determina los pasos 1 y 2 (todos son flujos de efectivo negativos) del procedimiento. Para el paso 4 se debe comparar la máquina 2 (el retador) con la máquina 1 (el defensor) sobre una base incremental. La relación VP es:
0 = -1500 + 300(PA,i*,8) + 400(PF,i*8)
La solución produce i* = 14.6%, la cual excede la TMAR de 13.5%. Por tanto, se elimina la máquina 1.
Los cálculos restantes se resumen en la siguiente tabla.
| Comparación utilizando la tasa de retorno | ||||
| Máquina | 1 | 2 | 3 | 4 |
| Costo inicial | -5000 | -6500 | -10000 | -15000 |
| CAO | -3500 | -3200 | -3000 | -1400 |
| V. S. | +500 | +900 | +700 | +1000 |
| Planes comparados | -- | 2 de 1 | 3 de 2 | 4 de 2 |
| Inversión incremental | -- | -1500 | -3500 | -8500 |
| Ahorros inc. | -- | +300 | +200 | +1800 |
| Salvamento inc. | -- | +400 | -200 | +100 |
| I*, % | -- | 14.6 | <0 | 13.6 |
| ¿Se justifica el incremento? | -- | Sí | No | Sí |
| Alternativa seleccionada | -- | 2 | 2 | 4 |
Cuando se comparan máquinas 3 y 2, i* <0%; por consiguiente se elimina la máquina 3.
La comparación de las máquinas 4 y 2 muestra que la tasa de retorno sobre el incremento es ligeramente mayor que la TMAR, favoreciendo la máquina 4. Puesto que no quedan alternativas adicionales disponibles, se selecciona la máquina 4.
Unidad 6
Modelos de Depreciación
6.1 Terminología de la depreciación
A continuación de definen algunos términos comúnmente utilizados en depreciación. La terminología es aplicable a corporaciones lo mismo que a individuos que poseen activos depreciables.
Depreciación: Es la reducción en el valor de un activo. Los modelos de depreciación utilizan reglas, tasas y fórmulas aprobadas por el gobierno para representar el valor actual en los libros de la Compañía.
Costo inicial: También llamado base no ajustada, es el costo instalado del activo que incluye el precio de compra, las comisiones de entrega e instalación y otros costos directos depreciables en los cuales se incurre a fin de preparar el activo para su uso. El término base no ajustada, o simplemente base, y el símbolo B se utilizan cuando el activo es nuevo.
Valor en libros: Representa la inversión restante, no depreciada en los libros después de que el monto total de cargos de depreciación a la fecha han sido restados de la base.
Periodo de recuperación: Es la vida depreciable, n, del activo en años para fines de depreciación (y del ISR). Este valor puede ser diferente de la vida productiva estimada debido a que las leyes gubernamentales regulan los periodos de recuperación y depreciación permisibles.
Valor de mercado: Es la cantidad estimada posible si un activo fuera vendido en el mercado abierto. Debido a la estructura de las leyes de depreciación, el valor en libros y el valor de mercado pueden ser sustancialmente diferentes.
Tasa de depreciación: También llamada tasa de recuperación, es la fracción del costo inicial que se elimina por depreciación cada año. Esta tasa puede ser la misma cada año, denominándose entonces tasa en línea recta, o puede ser diferente para cada año del periodo de recuperación.
Valor de salvamento: Es el valor estimado de intercambio o de mercado al final de la vida útil del activo. El valor de salvamento, VS, expresado como una cantidad en dólares estimada o como un porcentaje del costo inicial, puede ser positivo, cero ó negativo debido a los costos de desmantelamiento y de exclusión.
Propiedad personal: Está constituida por las posesiones tangibles de una corporación, productoras de ingresos, utilizadas para hacer negocios. Se incluye la mayor parte de la propiedad industrial manufacturera y de servicio: vehículos, equipo de manufactura, mecanismos de manejo de materiales, computadores, muebles de oficina, equipo de proceso de refinación y mucho más.
Propiedad real: Incluye la finca raíz y las mejoras a ésta y tipos similares de propiedad, por ejemplo: edificios de oficinas, estructuras de manufactura, bodegas, apartamentos. La tierra en sí se considera como propiedad real, pero no es depreciable.
Convención de medio año: Supone que se empieza a hacer uso de los activos o se dispone de ellos a mitad de año, sin importar cuándo ocurren realmente tales eventos durante el año.
6.2 Depreciación en línea recta
El modelo en línea recta es un método de depreciación utilizado como el estándar de comparación para la mayoría de los demás métodos. Obtiene su nombre del hecho de que el valor en libros se reduce linealmente en el tiempo puesto que la tasa de depreciación es la misma cada año, es 1 sobre el periodo de recuperación. Por consiguiente, d = 1 / n. La depreciación anual se determina multiplicando el costo inicial menos el valor de salvamento estimado por la tasa de depreciación d, que equivale a dividir por el periodo de recuperación n. En forma de ecuación queda de la siguiente manera:
Dt = (B - VS) / d = (B - VS) / n
Donde: t = año (1, 2, … n)
Dt = cargo anual de depreciación
B = costo inicial o base no ajustada
VS = valor de salvamento estimado
d = tasa de depreciación (igual para todos los años)
n = periodo de recuperación o vida depreciable esperada
Dado a que el activo se deprecia por la misma cuantía cada año, el valor en libros después de t años de servicio, VLt, será igual a la base no ajustada B menos la depreciación anual, multiplicado por t.
dt = 1 / n.
Ejemplo: Si un activo tiene un costo inicial de $50000 con un valor de salvamento estimado de $10000 después de 5 años, (a) calcule la depreciación anual y (b) calcule el valor en libros después de cada año, utilizando el método de depreciación en línea recta.
(a) La depreciación para cada año puede obtenerse mediante la ecuación:
Dt = (B - VS) / n = (50000 - 10000) / 5 = $8000 cada año.
(b) El valor en libros después de cada año t se calcula mediante la ecuación
VLt = V - tDt
VL1 = 50000 - 1*8000 = 42000
VL2 = 50000 - 2*8000 = 34000
VL3 = 50000 - 3*8000 = 26000
VL4 = 50000 - 4*8000 = 18000
VL5 = 50000 - 5*8000 = 10000 = VS
6.3 Depreciación por el método de la suma de los dígitos de los años
El método suma de los dígitos de los años (SDA) es una técnica clásica de depreciación acelerada que elimina gran parte de la base durante el primer tercio del periodo de recuperación. Esta técnica puede ser puede ser utilizada en los análisis de ingeniería económica, especialmente en las cuentas de depreciación de activos múltiples.
La mecánica del método comprende inicialmente encontrar S, la suma de los dígitos del total de años de 1 hasta el periodo de recuperación n. El cargo de depreciación para cualquier año dado se obtiene multiplicando la base del activo menos cualquier valor de salvamento (B - VS) por la razón del número de años restantes en el periodo de recuperación sobre la suma de los dígitos de total de años, S.
Dt = (años depreciables restantes / suma de los dígitos del total de años) (base - valor de salvamento) = (n - t + 1)/S (B - VS)
Donde S es la suma de los dígitos del total de años 1 hasta n.
S = "j = (n(n + 1))/2
El valor en libros para un año t se calcula como:
VLt = B - (t(n - t/2 + 0.5)/S) (B - VS)
La tasa de depreciación dt, que disminuye cada año para el método SDA, sigue el multiplicador en la ecuación:
dt = n - t + 1 / S
Ejemplo: Calcule los cargos de depreciación SDA para los años 1, 2 y 3 de un equipo electrónico con B = $25000, VS = $4000 y un periodo de recuperación de 8 años.
La suma de los dígitos del total de años es S = 36 y los montos de depreciación para los primeros 3 años son:
D1 = (8 - 1 + 1 / 36) * (25000 - 4000) = $4666.67
D2 = (8 - 2 + 1 / 36) * (25000 - 4000) = $4083.33
D1 = (8 - 1 + 1 / 36) * (25000 - 4000) = $3500.00
6.4 Depreciación por el método del saldo decreciente y saldo doblemente decreciente.
El método del saldo decreciente, conocido también como el método de porcentaje uniforme o fijo, es un modelo de cancelación acelerada. En términos simples, el cargo de depreciación anual se determina multiplicando el valor en libros al principio de cada año por un porcentaje uniforme, que se llamará d, en forma decimal equivalente. Por ejemplo, si la tasa de porcentaje uniforme es del 10% (es decir d = 0.10), la cancelación de depreciación para cualquier año dado será 10% del valor en libros al principio de ese año. El cargo de depreciación es más alto durante el primer año y disminuye para cada año que sucede.
El porcentaje de depreciación máximo permitido es el doble de la tasa en línea recta. Cuando se utiliza esta tasa, el método se conoce como saldo decreciente doble (SDD). Por tanto, si un activo tuviera una vida útil de 10 años, la tasa de recuperación en línea recta sería 1/n = 1/10 y la tasa uniforme para SDD sería d = 2/10 ó 20% del valor en libros. dmax = 2 / n
Ésta es la tasa utilizada para el método SDD. Otro porcentaje comúnmente utilizado para el método SD es 150% de la tasa en línea recta, donde d = 1.50/n.
La tasa de depreciación real para cada año t, relativa al costo inicial es:
dt = d(1 - d)t - 1
Para la depreciación SD o SDD, el valor de salvamento estimado no se resta del costo inicial al calcular el cargo de depreciación anual. Es importante recordar esta característica de los modelos SD y SDD.
Aunque los valores de salvamento no se consideran en los cálculos del modelo SD, ningún activo puede depreciarse por debajo de un valor de salvamento razonable, que puede ser cero. Si el valor en libros alcanza el valor de salvamento estimado antes del año n, no se puede efectuar ninguna depreciación adicional.
La depreciación para el año t, Dt, es la tasa uniforme, d, multiplicada por el valor en libros el final del año anterior. Dt = (d)VLt-1
Si el valor VLt-1 no se conoce, el cargo de depreciación puede calcularse como:
Dt = (d)B(1-d)t -1
El valor en libros en el año t puede determinarse de dos formas. Primero, utilizando la tasa uniforme d y el costo inicial B.
Así mismo, VLt , siempre puede determinarse para cualquier modelo de depreciación restando el cargo de depreciación actual del valor en libros anterior, es decir:
VLt = VLt -1 - Dt
El valor en libros en los métodos de saldo decreciente nunca llega a cero. Hay un VS implicado después de n años, el cual es igual a VL en el año n.
VS implicado = VLn = B(1-d)n
Si el VS implicado es menor que el VS estimado, el activo estará depreciado totalmente antes del final de su vida esperada.
También es posible determinar una tasa de depreciación uniforme implicada utilizando el monto VS estimado. Para VS > 0 d implicada = 1 -(VS/B)1/n
Ejemplo: Suponga que un activo tiene un costo inicial de $25000 y un valor de salvamento estimado de $4000 después de 12 años. Calcule su depreciación y su valor en libros para (a) año 1 y (b) año 4. (c) Calcule el valor de salvamento implicado después de 12 años para el modelo SDD.
Solución: Calcule primero la tasa de depreciación SDD, d.
d = 2/n = 2/12 = 0.1667
(a) para el primer año, se calcula la depreciación y el valor en libros utilizando las ecuaciones correspondientes:
D1 = (0.1667)(25000)(1 - 0.1667)1-1 = $4167.5
VL1 = 25000(1 - 0.1667)1 = $20832.50
(b) para el año 4, las ecuaciones correspondientes con d = 0.1667 dan como resultado:
D4 = 0.1667(25000)(1 - 0.1667)4 - 1 = 2411.46
VL4 = 25000(1 - 0.1667)4 = $12054.40
(c) El valor de salvamento implicado después del año 12 es:
VS implicado = 25000(1 - 0.1667)12 = $2802.57
Dado que el VS estimado de $4000 es mayor que $2802.57, el activo estará depreciado por completo antes de alcanzar su vida esperada de 12 años. Por consiguiente, una vez VLt , llega a $4000, no se permiten cargos adicionales de depreciación; en este caso, VL10 = $4036.02. Mediante la ecuación D11 = $672.80, por lo que el VL11 = $3362.22, que es menos del VS estimado de $4000. Entonces, durante los años 11 y 12, las cantidades de depreciación serán D11= $36.02 y D12 = 0.
Ejemplo: La compañía Hylsa adquirió una unidad para calificar metales controlada por computador por $80000. La unidad tiene una vida anticipada de 10 años y un VS de $10000. Utilice el método de saldo decreciente para desarrollar un programa de depreciación y los valores en libros para cada año.
Solución: Mediante la ecuación correspondiente, se determina la depreciación implicada utilizando el VS = 10000
d = 1 - (10000/80000)1/10 = 0.1877
| Año t | Dt | VLt |
| 0 | - | 80000 |
| 1 | 15016 | 64984 |
| 2 | 12197 | 52787 |
| 3 | 9908 | 42879 |
| 4 | 8048 | 34831 |
| 5 | 6538 | 28293 |
| 6 | 5311 | 22982 |
| 7 | 4314 | 18668 |
| 8 | 3504 | 15164 |
| 9 | 2846 | 12318 |
| 10 | 2318 | 10000 |
Unidad 7
Análisis Beneficio - Costo
El método de selección de alternativas más comúnmente utilizado por las agencias gubernamentales federales, estatales, provinciales y municipales para analizar la deseabilidad de los proyectos de obras públicas es la razón beneficio/costo (B/C). Como su nombre lo sugiere, el método de análisis B/C está basado en la razón de los beneficios a los costos asociada con un proyecto particular. Se considera que un proyecto es atractivo cuando los beneficios derivados de su implementación y reducidos por los beneficios negativos esperados exceden sus costos asociados. Por lo tanto, el primer paso en un análisis B/C es determinar cuáles de los elementos son beneficios positivos, negativos y costos. Se pueden utilizar las siguientes descripciones que deben ser expresadas en términos monetarios.
Beneficios (B) Ventajas experimentadas por el propietario.
Beneficios negativos (BN) Desventajas para el propietario cuando el proyecto bajo consideración es implementado.
Costos ( C ) Gastos anticipados por construcción, operación, mantenimiento etc. menos cualquier valor de salvamento.
Dado que el análisis B/C es utilizado en los estudios de economía por las agencias federales, estatales o urbanas, piénsese en el público como el propietario que experimenta los beneficios positivos y negativos y en el gobierno como en quien incurre en los costos. Por consiguiente, la determinación de si un renglón debe ser considerado un beneficio positivo o negativo o un costo, depende de quién es afectado por las consecuencias.
7.1 Cálculo de beneficios, desbeneficios y costo de un proyecto
Antes de calcular una razón B/C, todos los beneficios positivos, negativos y costos identificados deben convertirse a unidades comunes. La unidad puede ser un valor presente, valor anual o valor futuro equivalente, pero todos deben estar expresados en las mismas unidades.
Una vez que tanto los beneficios y desbeneficios, así como los costos estén expresados en las mismas unidades, la razón convencional B/C se calcula de la siguiente manera: B/C = (B - BN) / C.
Una razón B/C mayor o igual que 1.0, indica que el proyecto es económicamente ventajoso. En el análisis B/C, los costos no están precedidos por un signo menos.
La razón B/C modificada, incluye los costos de mantenimiento y operación (M&O) en el numerador, tratándolos en una forma similar a los beneficios negativos. El denominador, entonces, incluye solamente el costo de inversión inicial. Una vez que todas las cantidades están expresadas en términos de VP, VA ó VF, la razón B/C modificada se calcula como:
B/C modificada = [B - BN - C (M&O)] / Inversión inicial.
Como se consideró antes, cualquier valor de salvamento está incluido en el denominador como un costo negativo. Obviamente, la razón B/C modificada producirá un valor diferente que el arrojado por el método convencional B/C. Sin embargo, como sucede con los beneficios negativos, el procedimiento modificado puede cambiar la magnitud de la razón pero no la decisión de aceptar o rechazar.
Ejemplo: La fundación Vera internacional, una organización de investigación educativa sin fines de lucro, está contemplando una inversión de $1.5 millones en becas para desarrollar nuevas formas de enseñar a la gente las bases de una profesión. Las becas se extenderán por un periodo de 10 años y crearán un ahorro estimado de $500 mil anuales en salarios de facultad, matrículas, gastos de ingreso de estudiantes y otros gastos. La fundación utiliza una tasa de retorno del 6% anual sobre las becas otorgadas.
Puesto que el nuevo programa será adicional a las actividades en marcha, se ha estimado que se retirarán $200 mil de los fondos de otro programa para apoyar esta investigación educativa. Para hacer exitoso el programa, la fundación incurrirá en gastos de operación anual de $50 mil de su presupuesto regular M&O. Utilice los siguientes métodos de análisis para determinar si el programa se justifica durante un periodo de 10 años:
B/C convencional
B/C modificado
Análisis B - C
Solución: Utilice el valor anual como base de unidad común:
Beneficio positivo = $500000 anuales
Beneficio negativo = $200000 anuales
Costo M&O 1500000(A/P,6%,10[0.1359]) = $203850 anuales
B/C = 500000-200000 / 203850+50000 = 1.18 El proyecto se justifica ya que B/C > 1.0
B/C modificado = 500000-200000-50000 / 203850 = 1.23 El proyecto también se justifica por el método B/C modificado.
Ahora B es el beneficio neto y el costo M&O está incluido en C:
B-C = (500000-200000) - (203850+50000) = $46150; dado que B—C >0, nuevamente la inversión se justifica.
Ejemplo: El distrito local de autopistas está considerando rutas alternativas para una nueva avenida circunvalar. La ruta A, cuya construcción cuesta $4000000, proporcionará beneficios anuales estimados de $125000 a los negocios locales. La ruta B, que cuesta $6000000, puede proporcionar $100000 en beneficios anuales. El costo anual de mantenimiento es de $200000 par A y $120000 para B. Si la vida de cada avenida es de 20 años y se utiliza una tasa de interés del 8% anual, ¿Cuál alternativa debe seleccionarse con base en un análisis B/C convencional?
Solución: los beneficios en este ejemplo son $125000 para la ruta A y $100000 para la ruta B. El VA de los costos para cada alternativa es el siguiente:
VAA = -4000000(AP,8%,20[0.1019]) - 200000 = -607600
VAB = -6000000(AP,8%,20[0.1019]) - 120000 = -731400
La ruta B tiene un VA de costos más grande que la ruta A en $123800 por año pero ofrece menos beneficios en $25000. Por consiguiente, no hay necesidad recalcular la razón B/C para la ruta B puesto que esta alternativa es obviamente inferior a la ruta A. Además, si se ha tomado la decisión de que alguna de las rutas A o B debe ser aceptada, entonces no se necesitan otros cálculos y se selecciona la ruta A.
7.2 Comparación de alternativas mediante el análisis B/C
Al calcular la razón B/C para una alternativa dada, es importante reconocer que los beneficios y costos utilizados en el cálculo representan los incrementos o diferencias entre las dos alternativas. Éste será siempre el caso, puesto que algunas veces la alternativa de no hacer nada es aceptable.
Una vez que se calcula la razón B/C, un B/C > 1.0 significa que los beneficios extra justifican la alternativa de mayor costo. Si B/C < 1.0, la inversión o costo extra no se justifica y se selecciona la alternativa de costo más bajo. El proyecto de costo más bajo puede ser o no ser la alternativa de no hacer nada.
Ejemplo: Para la construcción de un nuevo segmento de la autopista interestatal se consideran dos rutas. La ruta N hacia el norte estaría localizada alrededor de 5 km del distrito empresarial central y requeriría distancias de viaje más largas por parte de la red conmutadora del tráfico local. La ruta S hacia el sur pasaría directamente a través del área central de la ciudad y aunque su costo de construcción sería más alto, reduciría el tiempo de viaje y la distancia para los usuarios de la red conmutadora de tráfico local. Suponga que los costos para las dos rutas son los siguientes:
| Ruta N | Ruta S | |
| Costo inicial | 10´000,000 | 15´000,000 |
| Costo anual de mantenimiento | 35,000 | 55,000 |
| Costo anual para el usuario | 450,000 | 200,000 |
Si se supone que las carreteras duran 30 años sin un valor de salvamento, ¿Cuál ruta debe seleccionarse con base en un análisis B/C utilizando una tasa de interés del 5% anual?
Solución: Como la mayoría de los flujos de efectivo están anualizados, la razón B/C estará expresada en términos de VA.
Los costos en el análisis B/C son los costos de construcción inicial y de mantenimiento:
VAN = 10000000(A/P,5%,30[0.0651]) + 35000 = 686000
VAS = 15000000(A/P,5%,30[0.0651]) + 55000 = 1031500
La ruta S tiene el VA más grande de los costos, de manera que es la alternativa que debe justificarse. El valor incremental del costo es: C = VAN - VAS = $345500 por año.
Los beneficios se derivan de los costos para el usuario de la carretera, ya que éstos son consecuencias para el público. Los beneficios para el análisis B/C no son en sí los costos para el usuario de la carretera, sino la diferencia si se selecciona la alternativa S.
Si se selecciona la ruta S, el beneficio incremental es el menor costo anual para el usuario de la carretera. Éste es un beneficio positivo para la ruta S, puesto que proporcionará los beneficios más grandes en términos de tales menores costos para el usuario de la carretera.
B = 450000 - 200000 = 250000 por año para la ruta S.
La razón B/C se calcula de la siguiente manera:
B/C = B-BN / C = 250000 / 345500 = 0.72
La razón B/C es menor que 1.0, indicando que los beneficios extra, asociados con la ruta S no se justifican. Por consiguiente, se selecciona la construcción de la ruta N.
7.3 Selección de alternativas utilizando análisis B/C incremental
Ejemplo: Considere las cuatro alternativas mutuamente excluyentes mostradas en la siguiente tabla. Aplique el análisis B/C incremental con el fin de seleccionar la mejor alternativa para una TMAR = 10% anual. Utilice un análisis VP.
| Estimaciones para cuatro ubicaciones posibles de construcción | ||||
| Ubicación | A | B | C | D |
| Costo de construcción $ | -200000 | -275000 | -190000 | -350000 |
| Flujo de efectivo anual $ | +22000 | +35000 | +19500 | +42000 |
| Vida, años | 30 | 30 | 30 | 30 |
Solución: Las alternativas se ordenan primero por costo de inversión inicial de menor a mayor (C, A, B, D) y se determinan los valores VP de los flujos de efectivo anuales. Calcule luego la razón B/C y elimine cualquier alternativa que tenga un B/C < 1.0.
| Alternativa | C | A | B | D |
| Costo de construcción | 190000 | 200000 | 275000 | 350000 |
| Flujo de efectivo | 19500 | 22000 | 35000 | 42000 |
| VP del flujo de efectivo | 183826 | 207394 | 329945 | 395934 |
| Razón B/C global | 0.97 | 1.03 | 1.20 | 1.13 |
| Proyectos comparados | - | - | B vs. A | D vs. B |
| Beneficio incremental | - | - | 122551 | 65989 |
| Costo incremental | - | - | 75000 | 75000 |
| Razón B/C incremental | - | - | 1.63 | 0.88 |
| Proyecto seleccionado | - | - | B | B |
Unidad 8
Análisis de reposición
8.1 Conceptos de retador y defensor en un análisis de reemplazo.
En la mayoría de los estudios de ingeniería económica se comparan dos o más alternativas. En un estudio de reposición, uno de los activos, al cual se hace referencia como el defensor, es actualmente el poseído (o está en uso) y las alternativas son uno o más retadoras. Para el análisis se toma la perspectiva (punto de vista) del asesor o persona externa; es decir, se supone que en la actualidad no se posee ni se utiliza ningún activo y se debe escoger entre la(s) alternativa(s) del retador y la alternativa del defensor en uso. Por consiguiente, para adquirir el defensor, se debe “invertir” el valor vigente en el mercado en este activo usado.
Dicho valor estimado de mercado o de intercambio se convierte en el costo inicial de la alternativa del defensor. Habrá nuevas estimaciones para la vida económica restante, el costo anual de operación (CAO) y el valor de salvamento del defensor. Es probable que todos estos valores difieran de las estimaciones originales. Sin embargo, debido a la perspectiva del asesor, todas las estimaciones hechas y utilizadas anteriormente deben ser rechazadas en el análisis de reposición.
Un hotel de playa, compró hace tres años una máquina para hacer hielo, de la más reciente tecnología, por $12000 con una vida estimada de 10 años, un valor de salvamento del 20% del precio de compra y un CAO de $3000. La depreciación ha reducido el costo inicial a su valor actual de $8000 en libros.
Un nuevo modelo de $11000, acaba de ser anunciado. El gerente del hotel estima la vida de la nueva máquina en 10 años, el valor de salvamento en $2000 y un CAO de $1800. El vendedor ha ofrecido una cantidad de intercambio de $7500 por el defensor de 3 años de uso. Con base en experiencias con la máquina actual, las estimaciones revisadas son: vida restante, 3 años; valor de salvamento, $2000 y el mismo CAO de $3000.
Si se realiza el estudio de reposición, ¿Qué valores de P, n, VS y CAO son correctos para cada máquina de hielo?
Solución: Desde la perspectiva del asesor, use solamente las estimaciones más recientes:
| Defensor | Retador |
| P = $7500 | P = $11000 |
| CAO = $3000 | CAO = $1800 |
| VS = $2000 | VS = $2000 |
| n = 3 años | n = 10 años |
El costo original del defensor de $12000, el valor de salvamento estimado de $2400, los 7 años restantes de vida y el valor de $8000 en libros no son relevantes para el análisis de reposición del defensor Vs. el retador.
Dado que el pasado es común a las alternativas, los costos pasados se consideran irrelevantes en un análisis de reposición. Esto incluye un costo no recuperable, o cantidad de dinero invertida antes, que no puede recuperarse ahora o en el futuro. Este hecho puede ocurrir debido a cambios en las condiciones económicas, tecnológicas o de otro tipo o a decisiones de negocios equivocadas. Una persona puede experimentar un costo perdido cuando compra un artículo, por ejemplo, algún software y poco después descubre que éste no funciona como esperaba y no puede devolverlo. El precio de compra es la cantidad del costo perdido. En la industria, un costo no recuperable ocurre también cuando se considera la reposición de un activo y el valor del mercado real o de intercambio es menor que aquel predicho por el modelo de depreciación utilizado para cancelar la inversión de capital original o es menor que el valor de salvamento estimado. El costo no recuperable de un activo se calcula como:
Costo no recuperable = Valor presente en libros - valor presente del mercado.
Si el resultado en la ecuación anterior es un número negativo, no hay costo no recuperable involucrado. El valor presente en libros es la inversión restante después de que se ha cargado la cantidad total de la depreciación; es decir, el valor actual en libros es el valor en libros del activo. Por ejemplo, un activo comprado por $100000 hace 5 años tiene un valor depreciado en libros de $50000. Si se está realizando un estudio de reposición y sólo se ofrecen $20000 como la cantidad de intercambio con el retador, según la ecuación anterior se presenta un costo no recuperable de 50000 - 20000 = 30000.
En un análisis de reposición, el costo no recuperable no debe incluirse en el análisis económico. El costo no recuperable representa en realidad una pérdida de capital y se refleja correctamente si se incluye en el estado de resultados de al compañía y en los cálculos del ISR para el año en el cual se incurre en dicho costo. Sin embargo, algunos analistas tratan de “recuperar” el costo no recuperable del defensor agregándolo al costo inicial del retador, lo cual es incorrecto ya que se penaliza al retador, haciendo que su costo inicial aparezca más alto; de esta manera se inclina la decisión.
Con frecuencia, se han hecho estimaciones incorrectas sobre la utilidad, el valor o el valor de mercado de un activo. Tal situación es bastante posible, dado que las estimaciones se realizan en un punto en el tiempo sobre un futuro incierto. El resultado puede ser un costo no recuperable cuando se considera la reposición. No debe permitirse que las decisiones económicas y las estimaciones incorrectas del pasado influyan incorrectamente en los estudios económicos y decisiones actuales.
En el ejemplo de la máquina de hielo, se incurre en un costo no recuperable para la máquina defendida si ésta es reemplazada. Con un valor en libros de $8000 y una oferta de intercambio de $7500, la ecuación correspondiente produce:
Costo no recuperable = 8000 - 7500 = $500
Los $500 nunca debieron agregarse al costo inicial del retador. Tal hacho penaliza al retador puesto que la cantidad de inversión de capital que debe recuperarse cada año es más grande debido a un costo inicial aumentado de manera artificialmente y es un intento de eliminar errores pasados en la estimación, pero probablemente inevitables.
8.2 Análisis de reemplazo utilizando un horizonte de planificación especificado
El periodo de estudio u horizonte de planificación es el número de años seleccionado en el análisis económico para comparar las alternativas de defensor y de retador. Al seleccionar el periodo de estudio, una de las dos siguientes situaciones es habitual: La vida restante anticipada del defensor es igual o es más corta que la vida del retador.
Si el defensor y el retador tienen vidas iguales, se debe utilizar cualquiera de los métodos de evaluación con la información más reciente.
Ejemplo: En la actualidad, Transportes Terrestres del Pantano, posee varios camiones de mudanza que se están deteriorando con mayor rapidez de lo esperado. Los camiones fueron comprados hace 2 años, cada uno por $60000. Actualmente, la compañía planea conservar los camiones durante 10 años más. El valor justo del mercado para un camión de 2 años es de $42000 y para un camión de 12 años es de $8000. Los costos anuales de combustible, mantenimiento, impuestos, etc. son de $12000.
La opción de reposición es arrendar en forma anual. El costo anual de arrendamiento es de $9000 (pago de fin de año) con costos anuales de operación de $14000. ¿Debe la compañía arrendar sus camiones si la TMAR es del 12%?
Solución: Considere un horizonte de planificación de 10 años para un camión que actualmente poseen y para un camión arrendado y realice un análisis VA para efectuar la selección.
| Defensor | Retador |
| P = 42000 | Costo de arrendar = 9000 anuales |
| CAO = 12000 | CAO = 14000 |
| VS = 8000 | No salvamento |
| n = 10 años | n = 10 años |
El defensor D tiene un valor justo del mercado de $42000, lo cual representa entonces su inversión inicial. El cálculo VAD es:
VAD = -P(A/P, i, n) + VS(A/F, i, n) - CAO
= -42000(AP,12,10[0.1770]) + 8000(AF,12,10[0.0570]) - 12000
= -$18978.00
La relación VAR para el retador C es:
VAR = -9000 - 14000 = -$23000
Es claro que la firma debe conservar la propiedad de los camiones, ya que VAD es numéricamente superior a VAR.
Ejemplo: Un municipio es propietario de un selector de material reciclable que ha utilizado durante 3 años. Con base en cálculos recientes, el activo tiene un VA de $5200 por año durante una vida restante estimada de 5 años. La reposición por un selector mejorado tiene un costo inicial de $25000, un valor de salvamento estimado de $3800, una vida proyectada de 12 años y CAO de $720. La ciudad utiliza una TMAR del 10% anual. Si se planea conservar el nuevo selector durante toda su vida estimada, ¿debe la ciudad reemplazar el antiguo selector?
Solución: Seleccione un periodo de estudio de 12 años correspondiente a la vida del retador. Suponga que el VA de $5200 del defensor es una buena estimación del costo equivalente anual para obtener el mismo nivel de selección de material reciclable después de los cinco años de vida restante del defensor.
VAD = -$5200
VAR = -25000(AP,10,12[0.1468]) + 3800(AF,10,12[0.0468]) - 720 = -$4212.16
La compra de un nuevo selector cuesta aproximadamente $1000 menos por año.
8.3 Análisis de reemplazo para retención adicional de un año
Normalmente se espera que un activo se conserve hasta el final de su vida de servicio económico o durante su vida útil estimada, si es diferente. Sin embargo, a medida que transcurre la vida de un activo que e posee actualmente, éste se deteriora, apareciendo entonces modelos disponibles más atractivos, modernos o mejorados; o las estimaciones de costo e ingreso original resultan ser significativamente diferentes de las cantidades reales. Entonces, una pregunta que se hace con frecuencia es: ¿Debe el activo ser reemplazado o conservarse en servicio durante 1, 2, 3 o más años? Buena pregunta si el activo ha estado en servicio durante todo el tiempo esperado; es decir, han transcurrido n años de servicio o la vida estimada ha expirado y parece que el activo tendrá más años de servicio. Dos opciones son posibles para cada año adicional. Seleccionar a un retador ahora o conservar al defensor durante un año más.
Para tomar la decisión de remplazar o conservar, no es correcto simplemente comparar el costo equivalente del defensor y el costo del retador durante el tiempo restante de servicio económico, vida útil anticipada, o algún número seleccionado de años más allá de cualquiera de estos dos números de años. En lugar de ello, se utiliza el procedimiento de valor anual donde:
VAR = Valor anual del retador
CD (1) = Estimación de costo del defensor para el año próximo (t = 1)
Si el costo de 1 año del defensor CD (1) es menor que el valor anual del retador, conserve al defensor un año más ya que su costo es menor.
Ejemplo: En general, Engineering Models, Inc., conserva su flota de auros al servicio de la compañía durante 5 años antes de su reposición. Debido a que los autos comprados con descuento hace exactamente 2 años se han deteriorado mucho más rápido de lo esperado, la gerencia se pregunta qué es más económico: reemplazar los autos este año por otros nuevos; conservarlos durante 1 año más y luego reemplazarlos; conservarlos durante dos años más y luego reemplazarlos; o conservarlos durante 3 años más hasta el final de sus vidas estimadas. Realice un análisis de reposición para i = 20% utilizando estos costos estimados.
| Auto actualmente poseído (defensor) | ||||
| Valor al principio de año | Costo anual de operación | Reposición posible (retador) | ||
| Año próximo 3 | 3800 | 4500 | Costo inicial | 8700 |
| Año próximo 4 | 2800 | 5000 | Costo anual | 3900 |
| Último año 5 | 500 | 5500 | Vida | 5 años |
| Vida restante | 3 | V. S. | 1800 | |
| V.S. después de 3 años ad. | 500 | |||
Solución: Calcule el VA para el retador durante 5 años.
VAR = -8700(AP,20,5[0.3344]) + 1800(AF,20,5[0.1344]) -3900 = -$6567.36
Calcule el costo del defensor para el próximo año (t = 1) utilizando un valor de $2800 como estimación del VS para el próximo año.
CD(1) = -3800(AP,20,1[1.2]) + 2800(AF,20,1[1.0]) -4500 = -$6260.00
Puesto que el costo CD(1) es menor que VAR, conserve los autos actuales durante el año siguiente.
Terminado el año próximo, para determinar si los autos deben conservarse aún otro año, siga con el análisis de los flujos de efectivo. Ahora, el valor de salvamento de $2800 en CD(1) es el costo inicial para el año t = 2. El costo del primer año CD (2) para el defensor es ahora:
CD (2) = -2800(AP,20 1[1.2]) + 500(AF,20,1[1.0]) - 5000 = -$7860.00
Ahora CD cuesta más que VAR = -$6567.36, de manera que debe calcularse el valor VAD para los dos años restantes de la vida del defensor.
VAD = - 2800(AP,20,2[0.6545]) + 500(AF,20,2[0.4545]) - 5000 -500(AG,20,2[0.4545]) = -$6832.60
Dado que el retador en VAR = -$6567.36 es también más barato para los 2 años restantes, es preferible seleccionarlo y reemplazar los autos actuales después de un año adicional (año 3) de servicio.
Unidad 9
Fundamentos de los impuestos
Cuando se realiza un análisis económico es razonable preguntar si dicho análisis debe hacerse antes o después de impuestos. Para una organización exenta de impuestos (Por ejemplo universitaria, estatal, religiosa, fundación o corporación sin fines de lucro), el análisis después de impuestos puede conducir o no a una decisión diferente de aquella basada en un análisis antes de impuestos. Aunque la alternativa seleccionada puede ser la misma, el análisis después de impuestos da estimaciones mucho mejores de los flujos de efectivo y de la tasa de retorno anticipada para una alternativa. Por estas razones, muchos analistas prefieren el análisis después de impuestos.
9.1 Definiciones tributarias
Ingreso bruto: IB, es el ingreso toral proveniente de fuentes que producen ingreso, incluyendo todos los renglones enumerados en la sección de ingresos de un estado de resultados. El término ingreso bruto ajustado se utiliza cuando se efectúan ciertos ajustes permisibles al ingreso bruto. Para los individuos, el ingreso bruto consta principalmente de sueldos, salarios, intereses, dividendos, regalías y ganancias de capital.
Gastos de operación: GO, incluyen todos los costos de corporaciones en los que se incurre en las transacciones de un negocio. Éstos son los costos de operación de la alternativa de la ingeniería económica.
Ingreso gravable: IG, es la cuantía en dinero sobre la cual se calculan los impuestos. Para las corporaciones, los gastos y la depreciación se restan del ingreso bruto para obtener el ingreso gravable.
IG = Ingreso bruto - gastos - depreciación
Tasa impositiva: Es un porcentaje, o equivalente decimal, del ingreso gravable debido en impuestos.
Impuestos = Ingreso gravable * tasa impositiva aplicable = IG * T
Utilidad neta: O ingreso neto, resulta en general, al restar los impuestos sobre la renta corporativa del ingreso gravable.
Pérdidas operacionales: Ocurre cuando una corporación incurre en pérdida neta en lugar de tener una utilidad neta.
Ganancia de capital: Es una cuantía del ingreso gravable en la cual se incurre cuando el precio de venta de un activo o propiedad depreciable excede el precio de compra original.
Pérdida de capital: Es el opuesto de la ganancia de capital. Si el precio de venta es menor que el valor en libros, la pérdida de capital es:
Pérdida de capital = Valor en libros - precio de venta.
Recuperación de la depreciación: Ocurre cuando la propiedad depreciable es vendida por una cuantía mayor que el valor en libros actual. El exceso es la recuperación de la depreciación, RD, y se grava como ingreso gravable ordinario. Se recupera depreciación si RD > 0 mediante el siguiente cálculo en el momento de la venta:
RD = precio de venta - valor en libros.
9.2 Fórmulas y cálculos tributarios básicos
El siguiente es un resumen de las relaciones utilizadas frecuentemente para los impuestos sobre la renta, corporativos e individuales. Estas relaciones se desarrollan para ayudar a comprender los elementos fundamentales del cálculo del impuesto sobre la renta. El flujo de efectivo generado por la venta de un activo puede afectar los impuestos.
| Relaciones generales para estimar impuestos sobre la renta corporativos anuales. | Relaciones generales para estimar impuestos sobre la renta individuales anuales. |
| Ingreso Bruto IB = ingreso de negocios + otros ingresos | Ingreso Bruto IB = salarios y sueldos + intereses y dividendos + otros ingresos |
| Ingreso Gravable IG = ingreso bruto - gastos de operación - depreciación | Ingreso Gravable IG = ingreso bruto - exenciones personales - deducciones por renglones o estándar |
| Impuesto Sobre la Renta Impuestos = IG * tasa impositiva | Impuesto Sobre la Renta Impuestos = IG * tasa impositiva |
Como se puede concluir, hay algunas diferencias significativas en la forma como se consideran las corporaciones y los individuos desde el punto de vista tributario. Las corporaciones pueden reducir el IB anual mediante todos sus gastos (de operación) legítimos del negocio, mientras que los individuos tienen cuantías determinadas de exenciones personales y deducciones específicas. Las exenciones personales son el individuo mismo, su esposa, sus niños y otros que dependen de el para el apoyo financiero principal.
La tasa impositiva T está basada en el principio de las tasas impositivas graduales, lo cual significa que las corporaciones e individuos pagan tasas más altas por ingresos gravables mayores. En las siguientes tablas se muestran los valores T para individuos y corporaciones.
| Programas de tasas del impuesto sobre la renta corporativa (mil = $ en millones) | ||||
| Límites IG | Rango IG | Tasa impositiva, T | Tasa máxima para el rango IG | Impuesto máximo incurrido |
| $1 - $50000 | $50000 | 0.15 | $7500 | $7500 |
| $50001 - 75000 | 25000 | 0.25 | 6250 | 13750 |
| 75001 - 100000 | 25000 | 0.34 | 8500 | 22250 |
| 100001-335000 | 235000 | 0.39 | 91650 | 113900 |
| 335001 - 10mil | 9.665mil | 0.34 | 3.2861mil | 3.4mil |
| Sobre10- 15mil | 5mil | 0.35 | 1.75mil | 5.15mil |
| Sobre 15 - 18.33mil | 3.33mil | 0.38 | 1.267mil | 6.417mil |
| Sobre 18.33mil | Ilimitado | 0.35 | Ilimitado | Ilimitado |
| Programa de tasas del impuesto sobre la renta individual para solteros y casados que declaran conjuntamente | ||
| Ingreso Gravable | ||
| Tasa impositiva | Declaración individual | Declaración de casados y conjunta |
| 0.15 | 0 - 23350 | 0 - 39000 |
| 0.28 | 23351 - 56550 | 39001 - 94250 |
| 0.31 | 56551 - 117950 | 94251 - 143600 |
| 0.36 | 117951 - 256500 | 143601 - 256500 |
| 0.396 | Sobre 256500 | Sobre 256500 |
Cada año el gobierno revisa y/o altera los rangos IG presentados en las tablas anteriores para considerar la inflación y otros factores. Esta acción se denomina indexación. Las tasas impositivas son alteradas también cuando se aprueba una nueva ley tributaria.
Debido a que las tasas marginales de impuestos cambian con IG, no es posible citar directamente el porcentaje de IG pagado en impuestos sobre la renta. Es útil calcular un porcentaje del IG total pagado, el cual se denomina tasa impositiva promedio y se calcula:
Tasa impositiva promedio = impuestos totales pagados/impuesto gravable total
TIP = Impuestos / IG
Hay impuestos federales, estatales y locales en mucha áreas. Para fines de simplicidad, la tasa impositiva en los estudios económicos es, con frecuencia, la tasa impositiva efectiva Te, que considera los impuestos federal, estatal y local en una sola cifra. Las tasas impositivas efectivas frecuentemente utilizadas están en el rango del 35% al 50%. Una razón par utilizar la tasa impositiva efectiva es que los impuestos estatales son deducibles para el cálculo del impuesto federal. La tasa efectiva impositiva como una fracción decimal es:
Te = tasa estatal + (1 - tasa estatal) (tasa federal)
Dado que las tasas impositivas graduales al nivel federal y estatal hacen que este cálculo sea difícil cuando se utilizan tasas marginales, es común utilizar una tasa impositiva gradual promedio para estimar Te, caso analizado en el siguiente ejemplo.
Ejemplo: Para un año particular, la división de software de Inteligencia de alta velocidad, tiene un ingreso bruto de $2750000, con un total de gastos y depreciación de $1950000. (a) Calcule los impuestos sobre la renta federales exactos de la Compañía. (b) Estime los impuestos totales federales y estatales si la tasa impositiva estatal es del 8% y se aplica una tasa federal única del 34%. (c) Estime la tasa impositiva promedio para el año tanto para los impuestos federales solamente como para los impuestos totales.
Solución:
(a) Calcule la ecuación IG y el impuesto exacto utilizando la tabla mostrada anteriormente
IG = 2750000 - 1950000 = 800000
Impuestos = (rango IG)(tasa impositiva marginal)
= 50000*0.15 + 25000* 0.25 + 25000*0.34 + 235000*0.39 + (800000 - 335000)*0.34 = 7500 + 6250 + 8500 + 91650 + 158100 = 272000.00
Un enfoque más rápido utiliza las cantidades en la columna 5 de la tabla correspondiente que están más cercanas al IG total y agrega el impuesto para el rango IG siguiente.
Impuestos = 113900 + (800000 - 335000)*0.34 = $272000.00
(b) Te = 0.08 + (1 - 0.08)(0.34) = 0.3928
Impuestos = IG * Te = 800000 * 0.3928 = 314240.00
(c) Tasas promedio:
Tasa impositiva promedio federal = 272000/800000 = 0.34 = 34%
Tasa impositiva promedio estatal = 314240/800000 = 0.3928 = 39.28%
Ejemplo: Omar y Ana presentaron una declaración de renta conjunta como pareja de casados el ISR. Durante el año, sus dos empleados les aportaron un ingreso combinado de $82000. Ellos adoptaron a su primer hijo durante le año y planean utilizar la deducción estándar de $7000 aplicable al año. Los dividendos e intereses ascendieron a $3550 y un canal de inversión reportó ganancias de capital por $550. Las exenciones personales son de $2500 cada una. Calcule la obligación impositiva federal exacta y la tasa impositiva federal promedio.
Solución: Ingreso Bruto = salarios + interés y dividendos + ganancias de capital
= 82000 + 3550 + 550 = 86100
Ingreso Gravable = ingreso bruto - exenciones - deducciones
= 86100 - 3*2500 - 7000 = 71600
Impuestos = 39000*0.15 + (71600 - 39000)*0.28 = $14978
Tasa impositiva promedio = 14978/71600 = 0.209 = 20.9%
9.3 Leyes tributarias para pérdidas y ganancias de capital
Todas las implicaciones de impuestos analizadas aquí son el resultado de la disposición de un activo de depreciación antes, durante ó después de su periodo de recuperación. La clave es el tamaño de la cantidad de salvamento (el precio de venta o valor de canje) relativo al valor en libros en el momento de la disposición del activo y relativo al costo inicial de éste.
Las definiciones de ganancia y pérdida de capital presentados en el punto anterior su utilizan en los análisis económicos para los activos depreciables cuando se adelanta un estudio después de impuestos.
El resultado final de las ventas de capital es una ganancia o pérdida de capital neta. Las pérdidas no reducen el ingreso gravable directamente, porque sólo permiten pérdidas de largo plazo para compensar las ganancias de largo plazo. En forma similar, las pérdidas de capital de corto plazo compensan las ganancias de corto plazo. Si hay una ganancia neta resultante (de largo o corto plazo), ésta se maneja como un ingreso gravable ordinario. Cualquier pérdida neta restante (por encima de las ganancias netas) en un año puede ser trasladada 3 años hacia atrás o 5 años hacia delante. Sin embargo, las perdidas netas crean un ahorro de impuestos para la compañía, siempre que en el año de ocurrencia haya ganancias en otras áreas contra las cuales pueda utilizarse la pérdida.
Las ganancias y pérdidas de corto plazo pueden ser importantes para fines del cálculo de impuestos. No obstante, puede ser la práctica corporativa no incluirlas en el análisis de inversiones económicas grandes, porque 1 año es corto tiempo comparado con la vida esperada de la mayoría de las alternativas. Pero, si se estima el tamaño de la pérdida de capital, ésta se utiliza definitivamente para reducir el tamaño de las ganancias de capital anticipadas, generando así ahorros de impuestos por el monto de la pérdida neta de capital multiplicado por la tasa impositiva (efectiva)
La recuperación de la depreciación (RD), puede ser incluida en los estudios después de impuestos. Sin importar su naturaleza, la suma total se grava como ingreso gravable ordinario.
Caso I. El precio de venta, es decir, el valor de salvamento realizado en el año t, excede el valor en libros en ese año. La RD es gravada a al tasa ordinaria. Un ejemplo sería vender un edificio por un valor mayor al valor corriente en libros.
Caso II. El precio de venta excede el costo inicia. Ahora hay componentes RD y ganancia de capital (GC) en el año t.
RD = costo inicial - valor en libros = B - VLt
Ganancia de capital = precio de venta - costo inicial.
IG = ingreso bruto - gastos de operación - depreciación + recuperación de depreciación + ganancias netas de capital - pérdidas netas de capital.
Cabe recordar que, si hay una pérdida neta de capital, se hace el supuesto de que habrá una ganancia de capital durante el mismo año en otra parte en la corporación para servir como compensación.
Ejemplo: El Sancho control systems, Inc., una recién formada compañía, espera obtener un ingreso bruto de $500000 y gastos de negocios y depreciación combinados de $300000 en el próximo año fiscal. Utilizando una tasa impositiva efectiva del 35%, calcule los impuestos sobre la renta esperados para las siguientes situaciones:
(a) Reposición de equipo de capital anticipada con ganancias de largo plazo de $25000 y pérdidas de largo plazo de $10000.
(b) Ganancias de largo plazo anticipadas específicas de $25000 y pérdidas de largo de $40000. Probablemente, la compañía tendrá ganancias en otras áreas.
Solución:
(a) La ganancia neta de largo plazo (GNLP) de $25000 - 10000 = 15000 se grava como ingreso ordinario. Calcule IG los términos relevantes según la ecuación vista con anterioridad.
IG = IB - gastos - depreciación + ganancia neta de capital
= 500000 - 300000 + 15000 = 215000
Impuestos = IG*Te = 215000*0.35 = 75250.00
(b) La pérdida neta de largo plazo (PNLP) de $40000 - 25000 = 15000 no está disponible para reducir directamente IG durante el año. Sin embargo, ésta puede ser utilizada para compensar ganancias en otras partes de la compañía, o la pérdida neta puede trasladarse 3 años hacia atrás o 5 años hacia delante para compensar ganancias en otros años fiscales. Puesto que se anticipan otras ganancias este año, habrá un ahorro de impuestos efectivo, ya que no se pagarán impuestos sobre algunas otras ganancias debido a esta compensación. Por consiguiente:
Impuestos = IG * Te = (500000 - 300000 - 15000) * 0.35 = $64750.00
Debido a otras ganancias durante el año, el monto del ahorro de impuestos incluido en la cuantía $64750.00 es: 15000 * 0.35 = $5250.00
9.4 Efectos tributarios de diferentes modelos de depreciación
El modelo de depreciación que se utilice afecta la cuantía de los impuestos incurridos. Los métodos acelerados, tales como SMARC (Sistema Modificado Acelerado de Recuperación de Costos), dan como resultado menos impuestos en los años iniciales del periodo de recuperación debido a una mayor reducción en el ingreso gravable.
Para evaluar el efecto tributario de los modelos de depreciación se utiliza el criterio de minimizar el valor presente de los impuestos totales. Es decir, para un periodo de recuperación n, se debe seleccionar el modelo de depreciación con el mínimo valor presente para impuestos, VP impuesto, donde:
VP impuesto = "(impuestos en el año t)(P/F,i,t)
Si se comparan ahora dos modelos de depreciación diferentes, cualesquiera, teniendo en cuenta las siguientes suposiciones: (1) la tasa impositiva constante de un solo valor, (2) el ingreso bruto excede cada monto de depreciación anual, (3) la recuperación de capital reduce el valor en libros hasta llegar al mismo valor de salvamento (comúnmente cero) y (4) el mismo periodo de recuperación en los años, entonces, para todos los modelos de depreciación se cumplen las siguientes aseveraciones:
Los impuestos totales pagados son iguales para todos los modelos de depreciación.
El valor presente de los impuestos, es menor para los modelos de depreciación acelerados.
Ejemplo: Se está llevando a cabo un análisis después de impuestos para una máquina nueva de $50000 propuesta para una línea manufacturera. La FEAI para la máquina se estima en $20000. Si se aplica un periodo de recuperación de 5 años, utilice el criterio de valor presente de los impuestos, una tasa impositiva del 35% y un retorno del 8% anual para comparar los siguientes elementos: depreciación en línea recta clásica, SDD y depreciación SMARC. Para fines de comparación utilice un periodo de 6 años consistentemente.
Solución: La tabla mostrada más adelante presenta un resumen de depreciación anual, ingreso gravable e impuestos para cada modelo. Para la depreciación clásica en línea recta con n = 5, Dt = 10000 durante 5 años y D6 = 0 (columna 3), el FEAI de $20000 está totalmente gravado en 35% en el año 6 para comparación con otros modelos.
El porcentaje SDD de d = 2/n = 0.40 se aplica para 5 años. El valor de salvamento implicado es $50000 - 46112 = $3888.00, de modo que no todos los $50000 son deducibles de impuestos. Los impuestos incurridos utilizando SDD son 3888*0.35 = 1360.80 más que para el modelo LR clásico.
| Línea recta | Saldo doblemente decreciente | SMARC | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| Año, t | FEAI | Dt | IG | Impuestos 0.35*(4) | Dt | IG | Impuestos 0.35*(7) | Dt | IG | Impuestos 0.35*(10) |
| 1 | 20000 | 10000 | 10000 | 35000 | 20000 | 0 | 0 | 10000 | 10000 | 3500 |
| 2 | 12000 | 8000 | 2800 | 16000 | 4000 | 1400 | ||||
| 3 | 7200 | 12800 | 4480 | 9600 | 10400 | 3640 | ||||
| 4 | 4320 | 15680 | 5488 | 5760 | 14240 | 4984 | ||||
| 5 | 2592 | 17408 | 6093 | 5760 | 14240 | 4984 | ||||
| 6 | 0 | 20000 | 7000 | 0 | 20000 | 7000 | 2880 | 17120 | 5992 | |
| Totales | $50000 | $24500 | $46112 | $25861* | $50000 | $24500 | ||||
| VP impuesto | $18386 | $18549 | $18162 | |||||||
* Mayor que otros valores puesto que hay un valor de salvamento implícito de $3888 no recuperado por el modelo SDD.
9.5, 9.6 y 9.7 Tabulación del flujo de caja después de impuestos
En los estudios de Ingeniería Económica los términos FEAI y FEDI se utilizan para representar flujos de efectivo anuales antes y después de impuestos respectivamente. Las relaciones entre estos dos términos y algunas relaciones pertinentes vistos anteriormente y que afectan de manera directa los impuestos sobre la renta corporativos, son:
FEAI = ingreso bruto - gastos de operación = IB - GO
IG = FEAI - depreciación + ganancias netas de capital - pérdidas netas de capital + recuperación de depreciación.
Impuestos = IG * T
FEDI = FEAI - impuestos.
Las cantidades en las relaciones anteriores son todas flujos de efectivo relacionados con impuestos reales, excepto por el término depreciación en la ecuación IG. La depreciación es la cantidad en libros puesto que representa la reducción en valor de la propiedad depreciable, pero ésta no es el flujo de efectivo real. No obstante, puesto que la depreciación es deducible de impuestos, ésta cambia el flujo de efectivo real reduciendo los impuestos sobre la renta, que son las salidas de efectivo reales. Cuando se realiza un análisis después de impuestos y se calcula el VP, el VA o la TR después de impuestos, se utilizan los valores FEDI en todos los cálculos.
Si la TR después de impuestos es importante en un análisis económico, pero los detalles del análisis TR antes de impuestos no lo son, lo común es aumentar (o inflar) la TR antes de impuestos para incorporar bien sea la tasa impositiva efectiva o marginal. Si una tasa impositiva de valor único está expresada en forma decimal, una aproximación del efecto de los impuestos en la TR del proyecto es:
TR después de impuestos = (TR antes de impuestos)(1 - tasa impositiva) =
= (TR antes de impuestos)(1 - T)
El valor T puede ser la tasa impositiva marginal aplicable o la tasa impositiva efectiva, Te. Por ejemplo, supóngase que la tasa impositiva efectiva estatal y federal de una compañía es 40% y que una TR después del 12% es la TMAR del mercado. La tasa impositiva TR implicada por un retorno del 12% después de impuestos se estima resolviendo la ecuación para la tasa de impuestos:
0.12 = (TR antes de impuestos) (1 - 0.40)
TR antes de impuestos = 0.12 / 0.60 = 0.20 = 20%
Este análisis se aplica tanto para corporaciones como para individuos.
Ejemplo: Además de las posiciones de gerencia corporativa, los Sánchez manejan un negocio de correo directo en la puerta de su hogar. Los resultados durante un año fiscal son:
| Recaudos del negocio | $60000 |
| Depreciación del equipo | $8000 |
| Gastos del negocio | $18500 |
| Ingreso de inversión del negocio | $5000 |
| Tasa impositiva estatal | 4% de IG |
La tasa de retorno representada por la inversión del negocio antes de impuestos es del 11%. Estime (a) el flujo de efectivo generado por el negocio y (b) el retorno después de impuestos de la inversión del negocio de los Sánchez.
Solución:
(a) El FEDI se calcula con la ecuación correspondiente para calcular el ingreso bruto, la tabla que se utiliza para determinar la tasa impositiva corporativa, la ecuación para la tasa impositiva efectiva las ecuaciones para estimar el FEDI.
FEAI = (IB) - gastos de operación = (ingresos + ingreso de inversión) - gastos = (60000 + 5000) - 18500 = $46500.00
IG = FEAI - depreciación = 46500 - 8000 = $38500.00
Te = 0.04 + (1 - 0.04) * 0.15 = 0.18
Impuestos = IG * Te = 38500 * 0.18 = $7084.00
FEDI = FEAI - impuestos = 46500 - 7084 = $39416.00
El negocio arrojó un flujo de efectivo real neto de $39416.00 después de impuestos.
(b) Utilice el 11% para el retorno antes de impuestos y 0.18 para la tasa impositiva efectiva en la ecuación de la TR después de impuestos.
El retorno de inversión después de impuestos = 0.11(1 - 0.18) = 0.09 = 9%
Los impuestos redujeron el retorno obtenido en la inversión del negocio del 11% al 9%.
Unidad 10
Análisis de sensibilidad
10.1 Enfoque de análisis de sensibilidad
El análisis económico utiliza estimaciones de sucesos futuros para ayudar a quienes toman decisiones. Dado que las estimaciones futuras siempre tiene alguna medida de error, hay imprecisión en las proyecciones económicas. El efecto de la variación puede determinarse mediante el análisis de sensibilidad. Algunos de los parámetros o factores comunes para hallar la sensibilidad son la TMAR, las tasas de interés, las estimaciones de vida, los periodos de recuperación para fines tributarios, todo tipo de costos, ventas y muchos otros factores. Este supuesto no es correcto por completo en situaciones del mundo real, pero es práctico puesto que en general no es posible para considerar en forma precisa las dependencias reales.
El análisis de sensibilidad, en sí mismo es un estudio realizado en general en unión con el estudio de ingeniería económica; determina la forma como una medida de valor (VP, VA, TR ó B/C) y la alternativa seleccionada se verán alteradas si un factor particular o parámetro varía dentro de un rango establecido de valores.
Generalmente, las variaciones en la vida, en los costos anuales y recaudos resultan de variaciones en el precio de venta, de operación a diferentes niveles de capacidad, de la inflación, etc. Por ejemplo, si un nivel de operación del 90% de la capacidad de sillas de una aerolínea se compara con el 50% en una ruta internacional nueva, el costo de operación y el recaudo por milla de pasajero aumentará, pero es probable que la vida anticipada disminuya solo ligeramente. De ordinario, para aprender cómo afecta el análisis económico la incertidumbre de las estimaciones, se estudian diversos parámetros importantes.
La graficación del VP, VA o TR versus el (los) parámetro (s) estudiado (s) es muy útil. Dos alternativas pueden compararse con respecto a un parámetro dado y calcularse el punto de equilibrio. Éste es un valor al cual las dos alternativas son equivalentes en términos económicos. Sin embargo, el diagrama del punto de equilibrio comúnmente representa sólo un parámetro por diagrama. Por tanto, se construyen diversos diagramas y se supone la independencia de cada parámetro.
Cuando se estudian diversos parámetros, un estudio de sensibilidad puede resultar bastante complejo. Éste puede realizarse utilizando un parámetro a la vez mediante un sistema de hoja de cálculo, un programa de computador preparado especialmente, o cálculos manuales. El computador facilita la comparación de múltiples parámetros y múltiples medidas de valor y el software puede representar gráficamente de manera rápida los resultados.
10.2 Determinación de la sensibilidad de las estimaciones
Al realizar un estudio de análisis de sensibilidad se puede seguir este procedimiento general, cuyos pasos son:
Determine cuál parámetro ó parámetros de interés podrían variar con respecto al valor estimado más probable.
Selecciones el rango probable de variación y su incremento para cada parámetro.
Seleccione la medida de valor que será calculada.
Calcule los resultados para cada parámetro utilizando la medida de valor como base.
Para interpretar mejor los resultados, ilustre gráficamente el parámetro versus la medida de valor.
Este procedimiento del análisis de sensibilidad debe indicar cuáles parámetros justifican un estudio más detenido o requieren la consecución de información adicional. Cuando hay dos alternativas o más, es mejor utilizar una medida de valor tipo monetario (VP ó VA) en el paso 3. Si se utiliza la TR, se requieren esfuerzos adicionales de análisis incremental entre alternativas.
Ejemplo: La Compañía “Enlatados agrícolas” está considerando la compra de un nuevo activo para el manejo automatizado del arroz. Las estimaciones más probables son un costo inicial de $80000, valor de salvamento de cero y una relación de flujo de efectivo antes de impuestos de la forma FEN = $27000 - 2000t anual (t = 1, 2,…n). La TMAR de la compañía varía entre el 10% y el 25% anual para los tipos diferentes de inversiones en activos. La vida económica de maquinaria similar varía entre 8 y 12 años. Evalúe la sensibilidad de VP y VA variando (a) el parámetro TMAR, a la vez que supone un valor ´n´ constante de 10 años y (b) el parámetro ´n´, mientras la TMAR es constante al 15% anual.
Solución:
(a) Siga el procedimiento anterior:
La TMAR, i, es el parámetro de interés.
Seleccione incrementos del 5% para evaluar la sensibilidad a la TMAR; el rango para i es del 10% al 25%.
Las medidas de valor son VP y VA.
Establezca las relaciones VP y VA. Por ejemplo, para i = 10%, utilice valores k de 1 a 10 para el flujo de efectivo:
VP = -80000 + 25000(P/A,10%,10[6.1446]) - 2000(P/G,10%,10[22.8913]) = $27832.40
VA = P(A/P,10%,10) = 27832.40(0.1627) = $4528.33
Las medidas de valor para los cuatro valores i en intervalos del 5% son:
| i | VP | VA |
| 10% | 27832.40 | 4528.33 |
| 15% | 11511.00 | 2294.14 |
| 20% | -961.70 | -229.37 |
| 25% | -10711.50 | -3000.29 |
En la siguiente figura se muestra una gráfica de la TMAR versus el VA. La pendiente negativa pronunciada indica que la decisión de aceptar la propuesta con base en VA es bastante sensible a variaciones en la TMAR. Si se establece la TMAR en el extremo en el extremo superior del rango, la inversión no es atractiva.
(b) Siga los pasos del procedimiento:
El parámetro es la vida ´n´ del activo.
Seleccione incrementos de 2 años para evaluar la sensibilidad a ´n´ durante el rango de 8 a 12 años.
Las medidas de valor son VP y VA.
Establezca las mismas relaciones VP y VA que en la parte (a) para i = 15%. Los resultados de las medidas de valor son:
| n | VP | VA |
| 8 | 7221.10 | 1609.58 |
| 10 | 11511.00 | 2294.14 |
| 12 | 13145.20 | 2425.29 |
En la siguiente figura se aprecia una gráfica no lineal de VA versus n. Ésta es una forma característica para el análisis de sensibilidad de un valor n. Como quiera que las medidas VP y VA son positivas para todos los valores de n, la decisión de invertir no se ve afectada en forma sustancial por la vida estimada.
10.3 Análisis de sensibilidad utilizando tres estimaciones
Es posible examinar en forma exacta las ventajas y desventajas económicas entre dos alternativas o más tomando en préstamo, del campo de la programación de proyectos, el concepto de elaborar tres estimaciones para cada parámetro: una estimación pesimista, una muy probable y una optimista.
Este enfoque nos permite estudiar la sensibilidad de la selección de las medidas de valor y de las alternativas dentro de un rango preestablecido de variación para cada parámetro. En general, cuando se calcula la medida de valor para un parámetro o alternativa particular se utiliza la estimación más probable para todos los demás parámetros.
Ejemplo: Suponga que usted es un ingeniero que está evaluando tres alternativas para las cuales un equipo de gerencia ha hecho tres estimaciones de estrategia, una pesimista (P), una muy probable (MP) y una optimista (O), para la vida, el valor de salvamento y los costos anuales de operación. Las estimaciones se presentan en la siguiente tabla a un nivel de alternativa por alternativa. Por ejemplo, la alternativa B tiene estimaciones pesimistas de VS = $500, CAO = $4000 y n = 2 años. Los costos iniciales se conocen, de manera que ellos tienen el mismo valor para todas las estrategias. Realice un análisis de sensibilidad para tratar de determinar la alternativa más económica utilizando el análisis VA y una TMAR del 12%.
| Alternativa | Estrategia | Costo inicial | VS | CAO | Vida (años) |
| A | P | -20000 | 0 | -11000 | 3 |
| A | MP | -20000 | 0 | -9000 | 5 |
| A | O | -20000 | 0 | -5000 | 8 |
| B | P | -15000 | 500 | -4000 | 2 |
| B | MP | -15000 | 1000 | -3500 | 4 |
| B | O | -15000 | 2000 | -2000 | 7 |
| C | P | -30000 | 3000 | -8000 | 3 |
| C | MP | -30000 | 3000 | -7000 | 7 |
| C | O | -30000 | 3000 | -3500 | 9 |
Solución: Para la descripción de cada alternativa en la tabla anterior, se calcula el VA de los costos. Por ejemplo, la relación VA para la estimación pesimista de la alternativa A es:
VA = -20000(A/P,12%,3[0.4163]) - 11000 = -19326.00
Los valores VA de las tres alternativas y sus respectivas estrategias se muestran a continuación:
| Valores VA alternativos | |||
| Estrategia | A | B | C |
| P | -19326.00 | -12639.65 | -19600.10 |
| MP | -14548.00 | -8228.80 | -13275.70 |
| O | -9026.00 | -5088.30 | -8927.90 |
Es claro que la alternativa que debe ser seleccionada es la B, ya que en la estrategia MP, tiene un costo menor que los de la estrategia optimista de las alternativas A y C.
10.4 Inflación y efecto de la inflación en los estimados
En los cálculos de recuperación del capital es particularmente importante que éstos incluyan la inflación debido a que el dinero de ahora debe recuperarse en dinero inflado futuro. Dado a que el dinero futuro tiene menos poder adquisitivo que el dinero de hoy, es obvio que se requerirá más dinero para recuperar la inversión presente. Este hecho sugiere el uso de la tasa de interés del mercado o la tasa inflada en la fórmula A/P. Por ejemplo, si se invierten $1000 hoy a una tasa de interés real del 10% anual cuando la tasa de inflación es del 8% anual, la cantidad anual del capital que debe recuperarse cada año durante 5 años en dinero corriente será:
A = 1000(A/P, 18.8%, 5[0.3256]) = $325.60
Por otra parte, el valor reducido del dinero a través del tiempo significa que los inversionistas pueden estar dispuestos a gastar menos dinero presente (de mayor valor) para acumular una cantidad determinada de dinero (inflado) futuro utilizando un fondo de amortización; o sea, se calcula un valor A. Esto sugiere el uso de una tasa de interés más alta, es decir, la tasa if , para producir un valor A más bajo en la fórmula A/P. El equivalente anual (cuando se considera la inflación) de la misma F = $1000 dentro de cinco años en dinero corriente de entonces es:
A = 1000(A/F, 18.8%, 5[0.1376])] = $137.60
Para comparación, la cantidad anual equivalente para acumular F = $1000 a una i real = 10% (antes de considerar la inflación), es 1000(A/F,10%,[0.1638]5) = $163.80. Por lo tanto, cuando F es fija, los costos futuros distribuidos uniformemente deben repartirse en el periodo de tiempo más largo posible, de manera que la inflación tenga el efecto de reducir el pago involucrado (137.60 Vs. 163.80).
Ejemplo: ¿Qué cantidad anual se requiere durante 5 años para acumular una cantidad de dinero con el mismo poder adquisitivo de compre que $680.58 hoy, si la tasa de interés del mercado es del 10% anual y la inflación es del 8% anual?
Solución: El número real de dinero inflado futuro requerido durante 5 años es:
F = (poder de compra actual) (1 + f)5 = 650.58 * (1.08)5 = $955.92
Por consiguiente, la cantidad real del depósito anual se calcula utilizando la tasa de interés inflada del mercado del 10%.
A = 955.92(A/F,10%,5[0.1638]) = $156.58
10.5 Modelos para considerar la inflación en la evaluación de las inversiones
Un método alternativo para estimar la inflación en un análisis de valor presente comprende el ajuste de las fórmulas mismas del interés para considerar la inflación. Considere la fórmula P/F, donde i es la tasa de interés real.
![]()
F (en dinero futuro) puede convertirse en dinero de hoy, utilizando la ecuación
![]()
= ![]()
Si el término i + f + if se define como if , la ecuación se convierte en:
![]()
La expresión if se denomina la tasa de interés inflada y se define como:
if = i + f + if donde
i = tasa de interés real.
f = tasa de inflación.
if = tasa de interés inflada.
Para una tasa de interés real del 10% anual y una tasa de inflación del 4% anual, la ecuación produce una tasa inflada del 14.4% (if = 0.10 + 0.04 + 0.10*0.04) = 0.144
Ejemplo: Un antiguo estudiante del ITSSNP desea efectuar una donación al Fondo de Desarrollo Estudiantil de su Alma Máter; ha ofrecido cualquiera de los tres planes siguientes:
Plan A. $60000 ahora.
Plan B. $15000 anuales durante 8 años empezando dentro de 1 año.
Plan C. $50000 dentro de 3 años y otros $80000 dentro de 5 años.
La única condición puesta para la donación es que la Institución acuerde gastar el dinero en investigaciones aplicadas relacionadas con el desarrollo de procesos de manufactura ambientales conscientes. Desde la perspectiva del Instituto, éste desea seleccionar el plan que maximiza el poder de compra del dinero recibido, de manera que ha pedido al profesor de Ingeniería económica evaluar los planes y considerar la inflación en los cálculos. Si la Institución desea obtener un 10% real anual sobre sus inversiones y se espera que la tasa de inflación promedie 3% anual, ¿Cuál plan debe aceptar?
Solución: El método de evaluación más rápido es calcular el valor presente de cada plan en dinero de hoy. Para los B y C, la forma más fácil de obtener el valor presente es mediante el uso de la tasa de interés inflada if.
if = 0.10 + 0.03 + 0.10*0.03 = 0.133 = 13.3%.
Calcule los valores VP con el uso apropiado de la ecuación correspondiente:
VPA = $60000.00
VPB = $15000(P/A,13.3%,8[4.7499]) = $71248.50
VPC = $50000(P/F,13.3%,3[0.6876]) + 80000(P/F,13.3%,5[0.5356]) = $77228.00
Dado que VPC es el mayor en términos de dinero de hoy, seleccione el plan C.
En los cálculos de valor futuro, la cantidad futura de dinero puede representar cualquiera de cuatro cantidades diferentes:
Caso 1. La cantidad real de dinero que será acumulada en el tiempo n.
Caso 2. El poder de compra, en términos de dinero de hoy, de la cantidad real de dinero acumulada en el tiempo n.
Caso 3. El número de pesos o dólares futuros requeridos en el tiempo n para mantener el mismo poder de compra de un peso o dólar hoy; es decir, no se considera el interés.
Caso 4. El número de dólares o pesos requeridos en el tiempo n para mantener el poder de compra y obtener una tasa de interés real determinada.
Debe ser claro que para el caso 1, la cantidad real de dinero acumulado se obtiene utilizando una tasa de interés determinada del mercado, la cual se identifica mediante if, ya que incluye la inflación.
Para el caso 2, el poder de compra de pesos futuros se determina utilizando la tasa de interés del mercado if para calcular F y luego se divide por (1 + f)n. la división por (1+f)n deflacta los dólares inflados. En efecto, este procedimiento reconoce que los precios aumentan durante la inflación, de manera que $1 en el futuro comprará menos bienes que $1 ahora. En forma de ecuación, el caso 2 es:
Suponga que $1000 obtienen la tasa de mercado del 10% de interés anual durante 7 años. Si la tasa de inflación para cada año es del 4%, la cantidad de dinero acumulado en 7 años, pero con el poder de compra de hoy, es:
Para comprender el poder de la inflación, considere lo siguiente. Si la inflación fuera nula (f se aproxima a 0), dentro de 7 años los $1000, a una tasa de interés del 10% crecerían a: F = 1000(F/P,10%,7[1.9487]) = $1948.70
Esto significa que el poder de compra de hoy y dentro de 7 años es igual. La inflación del 4% anual redujo en $467.85 el poder de compra.
También para el caso 2 podría determinarse en forma equivalente la cantidad futura de dinero acumulado con el poder de compra de hoy calculando la tasa de interés real y utilizándola en el factor F/P para compensar el poder de compra reducido de cada peso. La tasa de interés real puede obtenerse resolviendo para i en la ecuación:
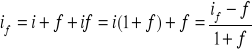
Dicha ecuación permite calcular la tasa de interés real a partir de la tasa de interés (inflada) del mercado. La tasa de interés real i representa la tasa a la cual el dinero presente se expandirá con su mismo poder de compra en dinero futuro equivalente. El uso de esta tasa de interés es apropiado al calcular e valor futuro de una inversión, especialmente una cuenta de ahorro o un fondo del mercado de dinero, cuando los efectos de la inflación deben ser considerados. Para la cantidad de $1000 de este caso, a partir de la ecuación de la tasa real, se tiene:
![]()
F = 1000(F/P,5.77%,7[1.4809]) = $1480.90
La tasa de interés establecida (en el mercado) del 10% anual ha sido reducida a menos del 6% anual debido a los efectos de la inflación. Una tasa de inflación mayor que la tasa de interés, es decir f > if , conduce a una tasa de interés real negativa.
El caso 3 también reconoce que los precios aumentan durante periodos inflacionarios y por consiguiente, adquirir un artículo en una fecha futura requerirá más dinero del requerido ahora. En términos simples, el dinero futuro vale menos, de modo que se requiere más.
Los cálculos para el caso 4 (mantener el poder de compra y ganar interés) consideran tanto los precios crecientes (caso 3) como el valor del dinero en el tiempo; es decir, debe obtenerse el crecimiento real del capital, los fondos deben crecer a una tasa igual a la tasa de interés real i más una igual a la tasa de inflación f. En consecuencia, para obtener una tasa de retorno real de 5.77% cuando la inflación es 4%, se utiliza if en las fórmulas. Utilizando la misma cantidad,
if = 0.0577 + 0.04 + 0.0577*0.04 = 0.10 = 10%
F = 1000(F/P,10%,7[1.9487]) = $1948.70
Este cálculo muestra que $1948.70 dentro de 7 años, serán equivalentes a $1000 ahora con un retorno real i = 5.77% anual e inflación de f = 4% anual.
La compañía de refrescos “El delirio”, desea determinar si debe pagar ahora o más tarde por el mejoramiento de sus instalaciones de producción. Si la compañía selecciona el plan A, se comprará el equipo necesario ahora por $20000. Sin embargo, si la compañía selecciona el plan I, no comprar ahora, la compra del equipo se diferirá durante 3 años y se espera que el costo aumente rápidamente hasta $34000. La TMAR no ajustada por la inflación es del 12% anual y la tasa de inflación se estima en 3% anual. Determine si la compañía debe comprar ahora o más adelante si (a) no se considera la inflación y (b) se considera la inflación.
Solución:
a) No se considera la inflación. La TMAR no ajustada por inflación es i= 12% anual y el costo del plan I es de $34000 dentro de 3 años.
FA = -20000(F/P,12%,3[1.4049]) = -$28098.00
FB = -$34000.00
Seleccione el plan A, ya que cuesta menos. Compre ahora.
b) Se considera la inflación. Primero, calcule la TMAR ajustada por inflación mediante la ecuación:
if = 0.12 + 0.03 + 0.12*0.03 = 0.1536 = 15.36%
FA = -20000(F/P,15.36%,3[1.5352]) = -$30704.00
FB = -$34000.00
Aún se selecciona el plan A, puesto que requiere menos dinero futuro equivalente.
Ingeniería económica
65
Descargar
| Enviado por: | Alase Puebla |
| Idioma: | castellano |
| País: | México |
