Maestro, Especialidad de Educación Infantil
Inducción
EJERCICIO 1
Los saludos
Para averiguar los saludos que se darán 20 personas vamos averiguar una fórmula primero con un nº más pequeño, para resolver el nº de saludos que se pueden dar.
Lo representaremos mediante un polígono, cada vértice representa una persona.
- Primero un polígono de 5 vértices.
- Ahora sacaremos una fórmula que lo confirme:
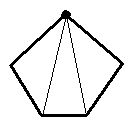
Desde cada vértice solo podemos sacar 2 diagonales porque las otras dos contiguas forman los lados y sobre él vértice mismo no es posible trazar ninguna línea. Es decir podemos unir 5 - 3 diagonales.
Sabemos que el total de diagonales es igual a la suma de consecutivos comenzando en 2 y que el último nº a sumar es el total de vértices (5) menos 2 ! 5 - 2. Luego la suma de extremos es igual a (5 - 2) + 2 = 5 por tantas sumas como parejas de extremos ()
Entonces si multiplicamos la suma de extremos por tantas diagonales como podemos unir (5 - 3) la fórmula final sería
Si resolvemos la fórmula: = 10/ 2 = 5 diagonales podemos trazar.
-
Hemos comprobado que sí da el mismo resultado, pero para verificarlo lo haremos con el siguiente polígono de 6 lados, es decir ¿cuántos saludos se darían 6 personas?
= = 18 / 2 = 9 saludos se darán
Si lo representamos gráficamente y contamos las diagonales vemos que el resultado es cierto.
-
Ahora resolvemos nuestro problema con 20 personas:
= = 340/ 2 = 170 saludos se darán 20 personas
¿Y si hubiese n personas?
Aplicamos a n la misma fórmula:
¿Y cuántas personas en una reunión que se hayan intercambiado 1225 saludos?
Si miramos el ejercicio b) sabemos que n representa a los vértices o lo que es lo mismo a las personas, y todo ello es igual a los saludos intercambiados que es nuestras incógnita. Sin embargo ahora la incógnita es n y tenemos el total de saludos que son 1225, si lo aplicamos obtenemos una ecuación:
Si la resolvemos despejaremos la incógnita y tendremos el resultado:
(2n - 6) 2n = 2450
(2n) 2n = 2450 + 6
22n = 2456
4n = 2456
n = = 614 personas se intercambiaran 1225 saludos.
EJERCICICO 2
CASTILLO DE CARTAS
-
Cada caseta esta compuesta por 3 cartas, y cada piso por una caseta más que el anterior, por tanto, podemos emplear la suma de extremos y enunciar una fórmula sencilla:
1·3 + 2·3 + 3·3 + -------------- + 10·3
-
2·3+(10-1)·3
-
1·3+10·3
Si sumamos todas las operaciones que son la mitad del total de sumandos 10/5 = 5 y restamos 10 cartas -que viene de que no ponemos cartas en la base de la torre porque se apoya directamente en el suelo, y es la más mayor compuesta por 10 casetas con 10 bases cada una- obtenemos el resultado.
Por tanto la fórmula a aplicar para hallar la solución teniendo en cuenta la que ya sabemos de la suma de números consecutivos (x - 1) · x/2; es la siguiente:
(1·3 + x·3) · x/2 - x
(1·3 + 10x·3) · 10/2 - 10 = 33·5 - 10 = 165 - 10 = 155 cartas necesitamos
¿Y para una torre de 62 pisos?
Aplicamos la fórmula del ejercicio anterior.
(1·3 + x·3) · x/2 - x
(1·3 + 62·3) · 62/2 - 62 = (190) · 31 - 62 = 5890 - 62 = 5828 cartas necesitamos
-
EJERCICIO 3
Los azulejos del ayuntamiento
-
Si contemplamos el dibujo en diagonal y contamos los azulejos del dibujo, comprobamos que hay por cada fila de 4 negros, 3 blancos. Si sumamos el cuadrado de los cuadrados negros + el cuadrado de los azulejos blancos, el resultado es 25.
42 + 32 = 16 + 9 = 25
- Si nos entretenemos a contar los azulejos del dibujo, vemos que efectivamente el resultado es 25 azulejos totales.
-
¿Y si tiene 149 azulejos de anchura, qué total tendrá?
Podemos entretenernos a contar los azulejos diagonales, pero teniendo en cuenta la deducción anterior, buscaremos una fórmula.
a = anchura n = azulejos negros b = azulejos blancos
N = total de azulejos
a = n + b ! sabemos que la suma de los 2 tipos de azulejos es igual a la anchura total
b = n - 1 ! siempre hay un azulejo mas negro por cada fila de blancos
N = n2 + b2 ! El total de azulejos es igual al cuadrado de 1 fila de negros + 1 fila de blancos
-
Ahora despejaremos incógnitas:
(n - 1) = b ; a = (n - 1) + n ! si tomamos el primer ejemplo resuelto:
7 = (n - 1) + n
7 + 1 = (n) + n
8 = 2n
8/2= n ; n = 4 azulejos negros, por tanto 4-1= 3, son los azulejos blancos.
Resolvemos:
Si ! N = n2 + b2
N = 42 + 32
N = 25
- Para comprobar que la fórmula es válida, probamos con menos azulejos de modo que podamos contar para comprobar, la anchura es 3:
3 = (n - 1) + n
3 + 1 = 2n
4 = 2n ; n = 4/2 = 2 azulejos negros y 2-1=1 blancos
N = n2 + b2
N = 22 + 12
N = 4 + 1
N = 5 azulejos totales ; si los contamos vemos que es cierto, por tanto la fórmula es válida.
- Por fin aplicamos la fórmula para el caso que se nos pregunta en el problema: anchura de 149 azulejos.
149 = (n - 1) + n
149 + 1 = n + n
150 = 2n
n = 150/2 = 75 azulejos negros y 75 - 4 = 74 azulejos blancos
N = n2 + b2
N = 752 + 742
N = 5476 + 5625 = 11.101 azulejos totales
* Una fórmula más sencilla y también válida sería:
Si N= anchura
(N + 1 / 2)2 + (N - 1 /2)2
EJERCICIO 4
LA TORRE
| La figura se compone de las siguientes piezas: |
|
|
|
|
|
|
|
|
|
|
| + |
|
| + |
|
| + |
|
| + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Por tanto, la fórmula es: 2×N×(ðððððð |
-Una torre de 6 metros de altura:
Para averiguar cuantos cubos necesitamos, sumaremos la altura de la torre (6) a la formula X+1.X y la dividimos entre 2 y luego lo multiplicamos por 4 paredes que tiene la torre:
6+[(5+1).5/2].4=6+30/2.4=6+15.4=6+60=66 cubos necesitamos
-Una torre de 12 cubos de altura:
12+[(11+1).11/2].4=12+132/2.11=12+66.11=12+264=276 cubos necesitamos
-Una torre de altura N
Si N es la altura, llamaremos M al número máximo de altura que tienen las 4 paredes que sujetaran la torreta, por tanto, aplicando las condiciones anteriores saber la suma de los números consecutivos M+1.M/2 y multiplicando por el número de paredes queda la siguiente formula:
N+ [(M+1).M/2].4 esta es la altura de una torre N
Otra forma posible de obtener el resultado:
Fórmula: n+2n(n-1) ! n= número de cubos en altura
a)n+2n(n-1)=6+12(6-1)=6+60=66 cubos
b)n+2n(n-1)=12+24.11=276 cubos
c)n+2n(n-1)
Mi fórmula también válida es:
N · [(N - 1) + 1] ·
EJERCICIO CUADRICULA
En esta cuadrícula de 8x8 tienes que averiguar cuántas
cuadrículas de todos los tamaños hay; las vas
buscando a ojo: 8
Cuadrículas de 8x8 : hay 1 : 1 al cuadrado
Cuadrículas de 7x7 : hay 4 : 2 al cuadrado
Cuadrículas de 6x6 : hay 9 : 3 al cuadrado
Cuadrículas de 5x5 : hay 16 : 4 al cuadrado
Cuadrículas de 4x4 : hay 25 : 5 al cuadrado 8
Cuadrículas de 3x3 : hay 36 : 6 al cuadrado
Cuadrículas de 2x2 : hay 49 : 7 al cuadrado
Cuadrículas de 1x1 : hay 64 : 8 al cuadrado
Asi puedes aplicar la formula que te da al principio
de suma de numeros consecutivos al cuadrado:
1 al cuadrado+2 al cuadrado+....+N al cuadrado es
igual a N(N+1}(2N+1}divido entre 6:
= 1224 / 6 = 204
El resultado sale 204 cuadrículas se pueden formar.
El resultado de cada suma de extremos es 33
Si trazamos diagonales entre los vértices y las contamos, obtenemos un resultado de 9; luego para un polígono de 5 vértices, obtenemos 5 diagonales !
N = 6 ! d = 5 ; es decir, si hubiera 6 personas, se darían 5 saludos.
Que si lo descomponemos en números consecutivos es igual a 2 + 3
Descargar
| Enviado por: | Lissy |
| Idioma: | castellano |
| País: | España |
