Matemáticas
Homotecia
Homotecia
Definición
Se llama homotecia de centro O y razón k (distinto de cero) a la transformación que hace corresponder a un punto A otro A´, alineado con A y O, tal que: OA´=k·OA. Si k>0 se llama homotecia directa y si k<0 se llama homotecia inversa.
Homotecias de centro el origen de coordenadas
En una homotecia de origen el centro de coordenadas se puede ver con facilidad la relación que existe entre las coordenadas de puntos homotéticos. Si se considera A(x,y) y su homotético A´(x´,y´) la relación que hay entre ellos es la siguiente: x´=kx y´=ky
Teorema de Tales. Semejanza de polígonos
Teorema de Tales
Si se cortan varias rectas paralelas por dos rectas transversales, la razón de dos segmentos cualesquiera de una de ellas es igual a la razón de los correspondientes de la otra. En el ejemplo de la escena Descartes siguiente tres rectas paralelas son cortadas por dos secantes r y s y puede comprobarse en todo momento qué valor alcanzan los segmentos determinados en estas dos rectas y sus cocientes, que son siempre iguales.
Semejanza de triángulos
Dos triángulos son semejantes cuando tienen sus ángulos iguales y sus lados proporcionales; es decir, si los triángulos ABC y A´B´C´ son semejantes se verifica:
A=A´ B=B´ C=C´ AB/A´B´=BC/B´C´=CA/C´A´=razón de semejanza
ESCALAS
La representación de objetos a su tamaño natural no es posible cuando éstos son muy grandes o cuando son muy pequeños. En el primer caso, porque requerirían formatos de dimensiones poco manejables y en el segundo, porque faltaría claridad en la definición de los mismos.
Esta problemática la resuelve la ESCALA, aplicando la ampliación o reducción necesarias en cada caso para que los objetos queden claramente representados en el plano del dibujo.
Se define la ESCALA como la relación entre la dimensión dibujada respecto de su dimensión real, esto es:
E = dibujo / realidad
Si el numerador de esta fracción es mayor que el denominador, se trata de una escala de ampliación, y será de reducción en caso contrario.
Basado en el Teorema de Thales se utiliza un sencillo método gráfico para aplicar una 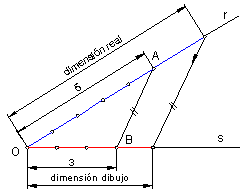
escala.
Véase, por ejemplo, el caso para E 3:5
1º) Con origen en un punto O arbitrario se trazan dos rectas r y
s formando un ángulo cualquiera.
2º) Sobre la recta r se sitúa el denominador de la escala
(5 en este caso) y sobre la recta s el numerador
(3 en este caso). Los extremos de dichos segmentos son A y B.
3º) Cualquier dimensión real situada sobre r será convertida en la del dibujo mediante una simple paralela a AB.
Efecto del dibujo a escala sobre las magnitudes lineales, el área y volumen
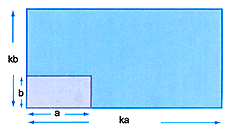
para conocer el efecto que produce el dibujo a escala sobre las magnitudes lineales, se analizará lo que ocurre cuando se amplía un rectángulo de dimensiones a y b hasta obtener un rectángulo de dimensiones ka y kb.
Obsérvese la relación que se establece entre el perímetro P del rectángulo original y el perímetro P´ del rectángulo ampliado:
P = 2a + 2b
y que P´ = 2(ka) + 2(kb)
Factorizando k, se obtiene:
P´ = k(2a + 2b)
Sustituyendo P´ = 2a + 2b, se llega a P´ = kP.
El perímetro P se transformó igual que la base y la altura del rectángulo.
A continuación se verá si ocurre lo mismo con las áreas.
| A = ab A´ = (ka) + (kb) A´ = k2ab A´ = k2(A) |
Si las longitudes se transforman con una escala k, entonces el área se transforma con una escala k2.
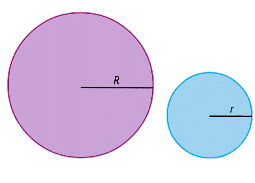
Véase lo que ocurre con la longitud de una circunferencia y con el área de un círculo:
Supóngase que el radio del círculo se transformó con una escala de k <1.
![]()
Si se comparan las dos medidas de las circunferencias, se tiene que:
![]()
La longitud de la circunferencia se transformó con una escala igual que la de la modificación del radio.
Para las áreas se tiene:
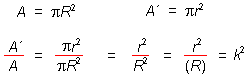
Nuevamente se observa que la razón o escala de las áreas es el cuadrado de la escala con la que se transforman las longitudes.
Resumen:
-
Efecto de las medidas angulares. Siempre que dos figuras o dos sólidos estén a escala, existe semejanza entre ellos; debiendo cumplirse la condición de tener sus ángulos homólogos iguales, pues la medida de un ángulo no la determina la longitud de los lados que lo forman, sino la abertura que hay entre dichos lados; además, sus lados homólogos son proporcionales.
-
Efecto en las medidas lineales y perímetros. Dos polígonos a escala son semejantes y cumplen, necesariamente, con dos condiciones: tener sus ángulos homólogos iguales y sus lados homólogos proporcionales.
-
Efecto de las áreas. La razón de las áreas de dos polígonos semejantes es igual al cuadrado de la escala dada.
-
Efecto en los volúmenes. La razón de los volúmenes de dos sólidos semejantes es igual al cubo de la escala dada.
MEDIA PROPORCIONAL
O media geométrica es cada uno de los términos medios de una proporción geométrica continua, o sea, cada uno de los términos medios de una proporción geométrica, cuando son iguales. Así, en la proporción 8:4::4:2 la media proporcional es 4.
TEOREMA
La media proporcional es igual a la raíz cuadrada del producto de los extremos.
Sea la proporción continua 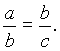
vamos a demostrar que ![]()
En efecto: ya sabemos por la propiedad fundamental que ac=bb, o sea, ac=b2.
Extrayendo la raíz cuadrada a ambos miembros, tenemos: ![]()
Y simplificando: 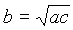
que era lo que queríamos demostrar.
EJEMPLO
En 
tenemos que ![]()
.
Cuarta proporcional es cualquiera de los cuatro términos de una proporción geométrica discreta. Así, en la proporción 8:16::5:10, cualquiera de estos cuatro términos es cuarta proporcional respecto de los otros tres.
EJEMPLO.
Hallar una cuarta proporcional de 20, 1/3 y 2/5.
Se forma una proporción geométrica con estas tres cantidades, poniendo de último extremo x y se despeja el valor de x: 20:1/3::2/5:x.
Despejando x: 
Sustituyendo el valor de x: 20:1/3::2/5:1/150.
Descargar
| Enviado por: | Kevin Noè Manrique Càmara |
| Idioma: | castellano |
| País: | México |
