Economía y Empresa
Función de producción
FUNCIÓN DE PRODUCCIÓN
Factores de Producción Productos
Tierra Bienes
Mano de obra Servicios
Capital
Materias primas
Función de Producción:
Relación tecnológica que indica cual es el máximo nivel de producto que se puede alcanzar, con una determinada cantidad de factores, para una tecnología dada
X = f (L, K, tierra, materias primas…..)
X = cantidad producida/unidad de tiempo
K,L,…= factores de producción/unidad de tiempo
L = mano de obra
K = capital
Plazo:
Determina el uso y combinación de los factores, depende de si los factores son fijos o variables
Corto plazo: periodo de tiempo donde al menos un factor esta fijo
X = f (L/K)
Largo plazo: periodo de tiempo donde todos los factores son variables
X = f (L, K)
El concepto de “plazo” no se refiere a tiempo cronológico, sino que depende exclusivamente del tiempo en que los factores fijos pasan a ser variables.
FUNCIÓN DE PRODUCCIÓN DE LARGO PLAZO
Dada la función:
X = f (L, K)
La producción podrá variar cambiando las cantidades tanto de L como de K. Para decidir la cantidad de L a contratar habrá que determinar K, o tamaño de planta óptimo de la empresa
Si el producto que lanza una empresa al mercado experimenta una demanda creciente, ésta deseará expandir la producción. De forma inmediata la empresa puede hacer que la mano de obra existente trabaje horas extraordinarias y también puede incrementar el número de empleados contratados. En un plazo de tiempo algo mayor, y si continúa la presión por parte del mercado, la empresa empezará a introducir nueva maquinaria y, a más largo plazo aún, puede incluso construir una nueva fábrica.
A largo plazo, las empresas tienen la posibilidad de alterar la cantidad de cualquiera de los factores que emplean en la producción. Precisamente, en economía, la distinción entre corto y largo plazo se establece únicamente atendiendo a la existencia o no de factores fijos.
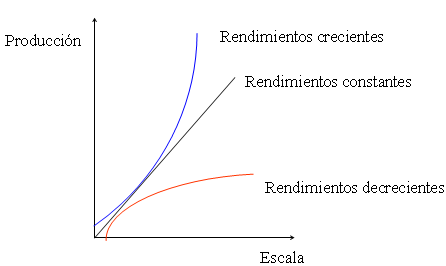
Las propiedades técnicas de la producción a largo plazo se establecen en torno al concepto de rendimientos de escala, y éste se aplica sólo al caso en que todos los factores varíen simultáneamente en la misma proporción.
Existen rendimientos o economías de escala crecientes cuando al variar la cantidad utilizada de todos los factores, en una determinada proporción, la cantidad obtenida el producto varía en una proporción mayor. Existen rendimientos constantes de escala cuando la cantidad utilizada de todos los factores y la cantidad obtenida de producto varía en la misma proporción.
Existen rendimientos de escala decrecientes cuando al variar la cantidad utilizada de todos los factores en una proporción determinada, la cantidad obtenida de producto varía en una proporción menor.
Los rendimientos de escala reflejan la respuesta del producto total cuando todos los factores se incrementan proporcionalmente.
Los niveles de producción Y1, Y2 e Y3 se proyectan en los ejes X1 y X2, se rota y se traspone la función obteniendo las isocuantas que se muestran a continuación.
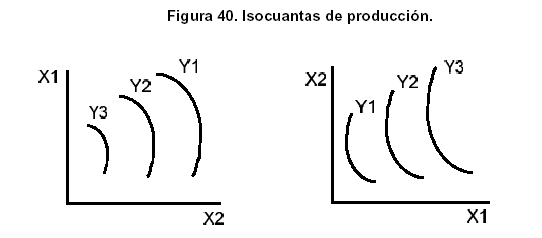
CURVAS ISOCUANTAS
Uno de los principales temas de la microeconomía es el papel central de la sustitución de agentes económicos. En la teoría del consumidor, los términos bajo los cuales los consumidores sustituyen un bien por otro se conceptualizan por las curvas de indiferencia. En la teoría de producción, las empresas sustituyen un insumo por otro y la herramienta grafica que capta estas relaciones técnicas es la curva isocuanta. Iso-cuanta significa “igual cantidad”. Una curva isocuanta conecta todas las posibles combinaciones de capital y trabajo que dan lugar a un mismo nivel de producción final. Mientras que las curvas de indiferencia reflejan las preferencias de los consumidores, las curvas isocuantas se refieren a la tecnología de producción de la empresa. Una diferencia importante entre las isocuantas y las curvas de indiferencia, es que las primeras se miden cardinalmente y las segundas se expresan en forma ordinal.
Grafica 1. La isocuanta
Las curvas isocuantas son una alternativa a la familia de curvas de producto total como representación grafica de la función de producción de la empresa, a largo plazo. En ambos casos - la familia de curvas de producto total y las curvas isocuantas - contienen la misma inf. Técnica sobre la relación de insumo y producto. Es útil comprender ambos métodos de presentación de la función de producción porque se utiliza para explicar la teoría de las empresas y sus implicaciones en el bienestar de la sociedad.
Las curvas denominadas Q0 en la grafica 1 es una curva isocuanta e incorpora todas las combinaciones posibles de capital y trabajo que son capaces de producir Q0 unidades de producción utilizando la mejor tecnología disponible. Se supone que el trabajo puede ser sustituido por el capital sin alterar el nivel de producción total. La curva es suave porque hemos supuesto que todos los insumos son infinitamente divisibles y adaptables.
Las curvas isocuantas se deriva de la función de producción Q = f (T, K), en la cual la producción se mantiene constante mientras varia el capital y el trabajo. Los estudios técnicos expresan las formas alternativas en que pueden ser combinados el trabajo y el capital para lograr un nivel de producción especifico. El nivel de producción es un parámetro de desplazamiento para la curva isocuanta; existe curva isocuanta diferente para cada nivel de producción.
Mapa de Isocuantas
El mapa de isocuantas o de curvas de isoproducto es la representación gráfica de la función de producción con la que trabajan los neoclásicos, o sea, es la forma gráfica que adopta la el supuesto de función de producción dada.
Características de las Isocuantas
-
Cada isocuanta es decreciente de izquierda a derecha lo cual implica que ninguna puede ser creciente ni paralela al eje de las ordenadas ni paralela al eje de las abscisas.
Supongamos que las siguientes gráficas reflejan isocuantas crecientes o paralelas a los ejes.
Como muestra la gráfica 1, es posible obtener el nivel de producción X1 utilizando TA del factor trabajo y KA del factor capital. Si la isocuanta fuera creciente, el punto B de coordenadas (TB, KB) arrojaría el mismo nivel de producción que la combinación de factores implicadas en el punto A.
Pero TB > TA y KB > KA, lo cual estaría implicando desperdicio de ambos factores productivos lo que significa el no cumplimiento de la condición de eficiencia técnica en materia de la utilización de los factores productivos.
Se ha caído en un absurdo técnico derivado del hecho de admitir que las isocuantas pueden ser crecientes.
Considérese la gráfica 2 donde la isocuanta aparece como paralela al eje de las ordenadas. El punto A (TA, KA) implica un cierto nivel de producción y el punto B (TB, KB) que contiene la misma cantidad del factor trabajo y mayor cantidad del factor capital (KB > KA) arrojaría como resultado el mismo nivel de producción lo cual estaría implicando, en este caso, desperdicio del factor capital. Análogamente, podemos señalar, en la gráfica 3 - donde se asume que la isocuanta puede ser paralela al eje de las abscisas - el punto C que implica la misma cantidad de capital que el punto A y mayor cantidad del factor trabajo estaría siendo técnicamente ineficiente.
-
Dos isocuantas no pueden cortarse.
Admitamos dos isocuantas decrecientes, la I y la II que se cortan en el punto A. Establecemos, a través de una paralela al eje de las ordenadas, dos puntos el D y el E donde el punto D pertenece a la isocuanta II y el punto E pertenece a la isocuanta I.
El punto A, por estar sobre la misma isocuanta que D, implica un nivel de producción de XII.
Asimismo, por estar sobre la misma isocuanta que E implica un nivel de producción XI. Por lo cual, se estaría cayendo en el absurdo de admitir que a una misma combinación de factores productivos (TA, KA) le corresponden niveles de producción diferentes. Ello no cumple con el concepto de función y, en especial, de función de producción.
Para no caer en el absurdo anterior, se debería cumplir que XI = XII. Si esto fuese así, las combinaciones representadas por los puntos E y D permitirían obtener el mismo nivel de producción. Pero en el punto D (KD, TD) se está utilizando la misma cantidad de factor trabajo que en el punto E (TD = TE) y una cantidad mayor del factor capital (KD > KE) lo cual implicaría que se viola el supuesto de eficiencia técnica.
-
Las isocuantas no pueden cortar los ejes.
Dicha característica emana del hecho de que, si bien existe sustituibilidad entre los factores productivos, dicha sustituibilidad es imperfecta, vale decir, no puede ser perfecta o total.
El punto A sobre el eje de las ordenadas estaría indicando que es posible obtener un nivel de producción X1 utilizando sólo el factor capital, o sea, TA = 0 y KA una magnitud positiva.
El punto B sobre el eje de las abscisas estaría indicando que es posible obtener el nivel de producción X1 utilizando solamente el factor productivo trabajo y nada del factor capital.
-
Cada isocuanta es convexa respecto al origen
Supongamos que nos encontramos en el punto A con una combinación (TA, KA). Por convención, definamos un punto B (TB, KB) que implica una unidad menos de capital y TB -TA unidades adicionales de trabajo. Similarmente, definamos un punto C (TC, KC) y un punto D que, también, están implicando por construcción una unidad menos de capital y TD - TC unidades adicionales de trabajo. Puede observarse que TB - TA es mucho menor que TD - TC.
La convexidad hacia el origen tiene relación con la característica de sustituibilidad imperfecta de los factores productivos y, en concreto, con la tasa de sustitución decreciente del factor productivo que se está utilizando en mayor grado (en nuestro ejemplo el factor trabajo a medida que nos movemos desde A hacia D pasando por B y C). La convexidad hacia el origen nos está indicando que, a medida que se tiene más de un factor y menos de otro, el factor relativamente escaso vale relativamente más, en términos del nivel de producción, que el factor relativamente abundante. En el ejemplo, si reducimos en una unidad el factor del cual se tiene menos, o sea, el capital cuando se pasa de C a D, para mantenernos en el mismo nivel de producción es necesario sustituirlo por una cantidad mucho mayor del factor que se tiene más. O a la inversa, que a medida que se tiene menos de un factor de producción, su tasa de sustitución en relación al otro va aumentando.
· El mapa de isocuantas es denso. Lo cual significa que por cada punto del plano pasa una isocuanta y solamente una isocuanta.
· A medida que nos trasladamos sobre la bisectriz del par de ejes coordenados alejándonos del origen, las sucesivas isocuantas que dicha bisectriz va cortando implican mayores niveles de producción.
FORMAS ISOCUANTAS
Se obtiene un conjunto de curvas de nivel, que se denominan isocuantas y representan todas las posibles combinaciones de diferentes insumos capaces de originar un mismo volumen de producción.
Las isocuantas se generan haciendo pasar una serie de planos paralelos al plano X1X2, a diferentes alturas, por la superficie de producción.
Estas curvas se pueden transferir a la superficie de insumos X1X2.
1.1. Relaciones de sustitución.
Se procede, en primer término, a determinar el grado y tipo de relación entre X1 y X2 para generar distintos niveles de Y.
Las formas de las isocuantas revelan rápidamente la intercambiabilidad de los factores utilizados y la posibilidad de sustitución de los mismos.
Las relaciones de sustitución más frecuentes son las siguientes:
SUSTITUCIONES PERFECTAS.
Las líneas rectas (Figura 41a) expresan sustituciones perfectas, en las que la elevación en el uso de un factor en perjuicio del otro no incrementa ni disminuye la cantidad producida.
La empresa puede utilizar indistintamente un factor u otro., responden a la expresión:
Y = f(X1, X2)= X1 + X2
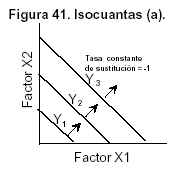
En un caso de cebo de corderos pueden sustituirse dos marcas de pienso de engorde de primera edad para conseguir un lechón de 20 Kg.;
Según Y = X1 + X2. Es indiferente que tipo de pienso aporto, sólo importan los consumidos y el peso final obtenido.
La característica más relevante de los factores sustitutivos es que las curvas de preferencia (isocuantas) presentan una pendiente constante.
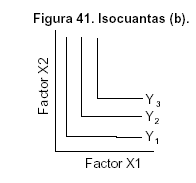
B) PROPORCIONES FIJAS.
La imposibilidad de sustitución genera curvas en ángulos rectos (Figura 41b) ya que se requiere un cierto nivel mínimo de cada factor para generar el producto. Se dispone de este tipo de tecnología cuando los factores de producción se combinan en la misma proporción. Las proporciones son fijas y no necesariamente 1:1 como en caso de los factores con sustituciones perfectas.
Y = f(X1, X2)= min {X1, X2}
Supongamos que disponemos de un rebaño de ovejas y establecemos un sistema de sincronización de celos y monta dirigida, sabemos tras múltiples experiencias que a cada lote de 20 ovejas hay que ponerle un morueco para obtener un porcentaje de fertilidad del 85%.
De nada sirve aumentar el número de machos porque se originan problemas de territorialidad y dominancia ni modificar el número de hembras con los consiguientes problemas de manejo. Por lo tanto el porcentaje de fertilidad va a depender del mínimo número de machos y hembras disponible y se expresa del siguiente modo: % fertilidad = min (ovejas, machos) Lo mismo ocurre con el aporte de oligoelementos, niveles de dosis medicamentosas, o con los sustitutivos lácteos.
C) SUSTITUCIONES COOB-DOUGLAS.
La más frecuente de las isocuantas en ganadería son las curvas Coob-Douglas en las que los factores se sustituyen entre si pero el reemplazo no es perfecto. Estos intercambios normalmente se ajustan a la ley de rendimientos decrecientes y a medida que se incrementa el consumo de un factor, es menor el crecimiento del producto. Responden a la expresión:
Y = f (X1, X2) = a x1b, x2c
"a" es la escala de producción y mide la cantidad que se puede generar si se utiliza una unidad de X1 y una unidad de X2.
"b" y "c" son parámetros que miden la sensibilidad de la producción ante variaciones de los factores, cuantifican la respuesta productiva.
Las isocuantas generalmente son convexas hacia el origen y la forma clásica de representación significa infinitas posibilidades de sustituciones entre factores para obtener un determinado nivel de producción; caso de los ingredientes de una ración para obtener un cerdo o un pollo de un determinado peso. Esta decisión de combinación de factores es de gran repercusión económica en la empresa ganadera y se aborda mediante la teoría económica.
LA TASA MARGINAL DE SUSTITUCIÓN TÉCNICA.
En la teoría de la producción, a medida que un productor desciende por la curva de isocuanta, sustituye un insumo por otro manteniendo constante el nivel de producción.
Un punto de gran importancia acá es la tasa a la cual el productor está dispuesto a sacrificar unidades de un insumo para utilizar unidades adicionales de otro.
¿Cuál es la tasa a la que el productor está dispuesto a sustituir un insumo o factor por otro, para mantener constante el nivel de producción que obtiene?
Esa tasa recibe el nombre de tasa marginal de sustitución técnica y mide el número de unidades en que disminuye un insumo, por unidad de incremento del otro, para que el nivel de producción permanezca constante. Dicha relación o tasa en un punto de la isocuanta es igual a la pendiente en valor absoluto de la isocuanta en ese punto. También es igual a la relación (cociente) del producto o rendimiento marginal de un factor respecto al producto marginal del otro. Como a medida que se utiliza más mano de obra y menos capital, el producto marginal de la mano de obra disminuye y el del capital aumenta, cuando se mantiene constante el nivel de producto, la misma es decreciente de izquierda a derecha. Esto conduce a emplear la convexidad de las isocuantas para su representación o a efectos de satisfacer el comportamiento decreciente.
La tasa marginal de sustitución técnica, es la pendiente de la curva de la isocuanta.
En la figura siguiente al productor le da lo mismo estar en el punto P utilizando A1 unidades de A y B2 unidades de B que en el punto Q donde utiliza A2 unidades de A y B1 unidades de B.
Para pasar desde el punto P al punto Q el productor esta dispuesto a dejar de utilizar B2B1 de B para utilizar A1A2 de A.
Por los tanto, la tasa a la cual está dispuesto a sustituir B por A es:
Este cociente mide el número de unidades que el productor está dispuesto a ceder
de B para utilizar una unidad adicional de A. Recibe el nombre de Tasa Marginal de Sustitución Técnica de B por A. Se simboliza de la siguiente manera:
Cuando las variaciones alrededor de un punto son infinitesimalmente pequeñas, la tasa marginal de sustitución técnica de B por A es la pendiente de la curva de isocuanta en ese punto.
Debido a que las curvas de isocuanta al igual que las curvas de indiferencia tienen pendiente negativa, cuando B disminuye A aumenta y viceversa. Esto significa que el signo de la tasa marginal de sustitución técnica es siempre negativo.
Otra característica de la tasa marginal de sustitución técnica es que, la misma es decreciente, en valor absoluto, a medida que el productor desciende sobre su curva de isocuanta. Esta característica puede analizarse de la misma manera en que se hizo para las curvas de indiferencia, razón por la cual obviamos su demostración.
Se observa para la isocuanta:
* Los puntos A, B, C, y D de la isocuanta, así como las rectas tangentes a la curva
de nivel en cada punto.
* El valor de la tasa marginal exacta de sustitución es el de la pendiente de cada recta, o lo que es igual la tangente trigonométrica del ángulo que cada recta forma
con el eje de abscisas.
* La disminución de la tasa de sustitución desde el punto A (a de 90º y la tangente es ¥) al punto C (a de 0º y la tangente es 0), por lo que la tasa marginal de sustitución oscila desde infinito a cero.
De modo sintético puede expresarse:
Cuando los ángulos de las rectas tangentes a determinadas combinaciones de producción sean mayores de 90º, la producción está situada en zona racional, con rendimientos decrecientes, y los factores son sustitutivos.
Cuando la recta tangente en cada punto presente un ángulo inferior a 90º, la producción se sitúa en zona de irracionalidad técnica, con rendimientos crecientes o negativos y los factores frecuentemente son complementarios.
K
T
Q2
Q1
Q0
Descargar
| Enviado por: | Chio |
| Idioma: | castellano |
| País: | Perú |
