Sistemas de telecomunicación e informáticos
Física
MAGNITUDES FISICAS
El gran físico inglés Lord Kelvin consideraba que solamente puede aceptarse como satisfactorio nuestro conocimiento si somos capaces de expresarlo mediante números. Aun cuando la afirmación de Lord Kelvin tomada al pie de la letra supondría la descalificación de valiosas formas de conocimiento, destaca la importancia del conocimiento cuantitativo, particularmente en el tipo de ciencia que él profesaba.
La operación que permite expresar una propiedad o atributo físico en forma numérica es precisamente la medida.
Magnitud, cantidad y unidad
La noción de magnitud está inevitablemente relacionada con la de medida. Se denominan magnitudes ciertas propiedades o aspectos observables de un sistema físico que pueden ser expresados en forma numérica. En otros términos, las magnitudes son propiedades o atributos medibles.
La longitud, la masa, el volumen, la fuerza, la velocidad, la cantidad de sustancia son ejemplos de magnitudes físicas. La belleza, sin embargo, no es una magnitud, entre otras razones porque no es posible elaborar una escala y mucho menos un aparato que permita determinar cuántas veces una persona o un objeto es más bello que otro.
La sinceridad o la amabilidad tampoco lo son. Se trata de aspectos cualitativos porque indican cualidad y no cantidad.
En el lenguaje de la física la noción de cantidad se refiere al valor que toma una magnitud dada en un cuerpo o sistema concreto; la longitud de esta mesa, la masa de aquella moneda, el volumen de ese lapicero, son ejemplos de cantidades.
Una cantidad de referencia se denomina unidad y el sistema físico que encarna la cantidad considerada como una unidad se denomina patrón.
La medida como comparación
La medida de una magnitud física supone, en último extremo, la comparación del objeto que encarna dicha propiedad con otro de la misma naturaleza que se toma como referencia y que constituye el patrón.
La medida de longitudes se efectuaba en la antigüedad empleando una vara como patrón, es decir, determinando cuántas veces la longitud del objeto a medir contenía a la de patrón. La vara, como predecesora del metro de sastre, ha pasado a la historia como una unidad de medida equivalente a 835,9 mm. Este tipo de comparación inmediata de objetos corresponde a las llamadas medidas directas.
Con frecuencia, la comparación se efectúa entre atributos que, aun cuando están relacionados con lo que se desea medir, son de diferente naturaleza. Tal es el caso de las medidas térmicas, en las que comparando longitudes sobre la escala graduada de un termómetro se determinan temperaturas. Esta otra clase de medidas se denominan indirectas.
Tipos de magnitudes
Entre las distintas propiedades medibles puede establecerse una clasificación básica. Un grupo importante de ellas quedan perfectamente determinadas cuando se expresa su cantidad mediante un número seguido de la unidad correspondiente. Este tipo de magnitudes reciben el nombre de magnitudes escalares. La longitud, el volumen, la masa, la temperatura, la energía, son sólo algunos ejemplos.
Sin embargo, existen otras que precisan para su total definición que se especifique, además de los elementos anteriores, una dirección o una recta de acción y un sentido: son las llamadas magnitudes vectoriales o dirigidas. La fuerza es un ejemplo claro de magnitud vectorial, pues sus efectos al actuar sobre un cuerpo dependerán no sólo de su cantidad, sino también de la línea a lo largo de la cual se ejerza su acción.
Al igual que los números reales son utilizados para representar cantidades escalares, las cantidades vectoriales requieren el empleo de otros elementos matemáticos diferentes de los números, con mayor capacidad de descripción. Estos elementos matemáticos que pueden representar intensidad, dirección y sentido se denominan vectores.
Las magnitudes que se manejan en la vida diaria son, por lo general, escalares. El dependiente de una tienda de ultramarinos, el comerciante o incluso el contable, manejan masas, precios, volúmenes, etc., y por ello les es suficiente saber operar bien con números. Sin embargo, el físico, y en la medida correspondiente el estudiante de física, al tener que manejar magnitudes vectoriales, ha de operar, además, con vectores.
MAGNITUD DE VECTORES
En matemáticas, cantidad que tiene magnitud, dirección y sentido al mismo tiempo. Por ejemplo, si una cantidad ordinaria, o escalar, puede ser una distancia de 6 km, una cantidad vectorial sería decir 6 km norte. Los vectores se representan normalmente como segmentos rectilíneos orientados, como B en el diagrama que se muestra a continuación; el punto O es el origen o punto de aplicación del vector y B su extremo. La longitud del segmento es la medida o módulo de la cantidad vectorial, y su dirección es la misma que la del vector.
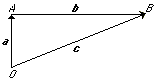
El uso sencillo de los vectores así como los cálculos utilizando vectores quedan ilustrados en este diagrama, que muestra el movimiento de una barca para atravesar una corriente de agua. El vector a, u A, indica el movimiento de la barca durante un determinado periodo de tiempo si estuviera navegando en aguas tranquilas; el vector b, o $, representa la deriva o empuje de la corriente durante el mismo periodo de tiempo. El recorrido real de la barca, bajo la influencia de su propia propulsión y de la corriente, se representa con el vector c, u B. Utilizando vectores, se puede resolver gráficamente cualquier problema relacionado con el movimiento de un objeto bajo la influencia de varias fuerzas.
Este método de resolución de problemas, conocido como adición vectorial, se lleva a cabo según se explica a continuación. Un vector que representa una fuerza se dibuja empezando por el origen O en la dirección y con el sentido apropiados. La longitud del vector es proporcional a su valor real según una escala determinada, que puede ser un cierto número de centímetros por cada kilómetro. En el dibujo anterior, la velocidad al remar es de 2,2 km/h, el tiempo transcurrido es 1 hora y la escala es 1 cm por cada km. Por tanto, el vector A mide 2,2 cm y representa 2,2 km. La velocidad de la corriente del río es de 6 km/h, y se representa con el vector $ que mide 6 cm, lo que indica que la corriente recorre una distancia de 6 km en una hora. Este segundo vector se dibuja con su origen en el extremo del vector a y en dirección paralela al movimiento de la corriente. El punto B, extremo del segundo vector, es la posición real de la barca después de una hora de viaje, y la distancia recorrida es la longitud del vector c, u B (en este caso, unos 6,4 km).
Los problemas de adición y sustracción de vectores, como el anterior, se pueden resolver fácilmente utilizando métodos gráficos, aunque también se pueden calcular utilizando la trigonometría. Este tipo de cálculos es de gran utilidad para resolver problemas de navegación y movimiento en general; también se utilizan en la mecánica y otras ramas de la física. En las matemáticas de nuestros días, un vector es considerado como un conjunto ordenado de cantidades con determinadas reglas para su utilización. El análisis vectorial (es decir, el álgebra, la geometría y el cálculo de cantidades vectoriales) aparece en las matemáticas aplicadas en todos los campos de la ciencia e ingeniería.
CONVERSIONES DE UNIDADES
Longitud
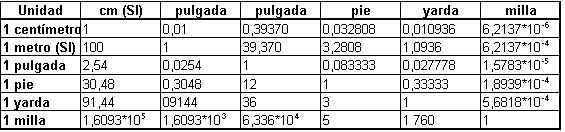
Superficie
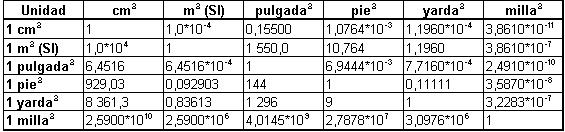
Volumen
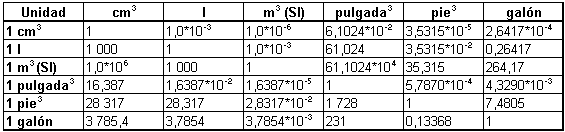
Masa
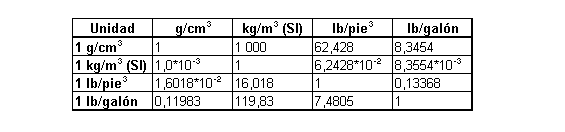
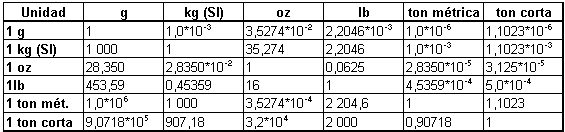
Densidad
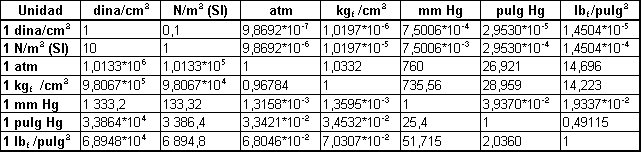
Presión
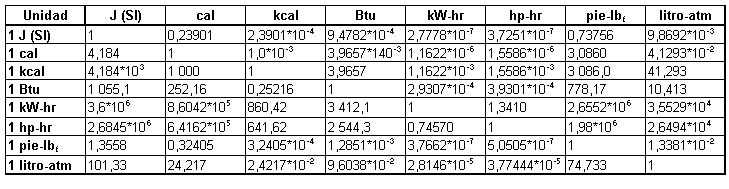
Energía
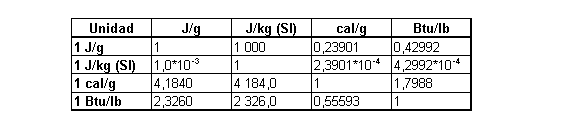
Energía Específica
Capacidad Calorífica y Entropía Específica
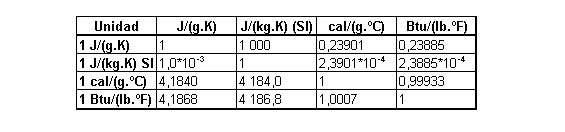

Potencia
La Notación Científica
HISTORIA:
Para los griegos a. C. 10.000 era un número gigante, no así para los matemáticos de ese tiempo. Arquímedes, 200 a. C. se preocupa por calcular el número de granos de arena necesarios para llenar el Cosmos y calcula que se necesitarían 1063. Pero esas ideas no formaban parte del pensamiento del hombre común.
Cuando el hombre empieza a viajar, a apreciar las distancias entre los países o a pensar en las distancias entre los astros, en las estrellas del cielo, en cuantos años tiene la Tierra, van apareciendo en su mente los números grandes. En un principio fue el millón “los millonarios”. Ahora ya esos números han quedado atrás.
¿Que es la Notación Científica?
En la ciencia, es común trabajar con números muy grandes y muy pequeños. Por ejemplo, el diámetro de una glóbulo rojo es 0.0065 cm, la distancia de la tierra al sol es 150,000,000 Km, y el número de moléculas en 1 g de agua es 33,400,000,000,000,000,000,000. Es engorroso trabajar con números tan largos, así que medidas como estas son generalmente escritas usando la abreviación llamada la notación científica.
Cada cero en los números de arriba representa un múltiplo de 10. Por ejemplo, el número 100 representa 2 múltiplos de 10 (10.x 10 = 100. En la notación científica, 100 puede ser escrito como 1 por 2 múltiplos de 10:
100 = 1 x 10 x 10 = 1 x 102 (en la notación científica)
La notación científica es una manera simple de representar los números grandes ya que el exponente sobre el 10 (2 en el ejemplo de arriba) le dice cuántos lugares hay que mover el decimal del coeficiente (el 1 en el ejemplo de arriba) para obtener el número original. En nuestro ejemplo, el exponente 2 nos dice que hay que mover el decimal a la derecha dos lugares para generar el número original.
![]()
La notación científica puede aún ser usada hasta cuando el coeficiente es otro número que el 1. Por ejemplo:

Esta abreviación también puede ser usada con números muy pequeños. Cuando la notación científica se usa con números menores a uno, el exponente sobre el 10 es negativo, y el decimal se mueve hacia la izquierda, en vez de hacia la derecha. Por ejemplo:

Por consiguiente, usando la notación científica, el diámetro de un glóbulo rojo es 6.5.x 10-3 cm, la distancia de la tierra al sol es 1.5 x 108km y el número de moléculas en 1 g de agua es 3.34 x 1022.
En síntesis:

Para comprender mejor la notación observa:
7280000 = 7,28 · 106
= 72,8 · 105
= 728 · 104
= 7280 · 103
= 72800 · 102
= 728000 · 101
=7280000 · 100 (100=1)
Podría decirse que multiplicar por una potencia de 10 “compensa” el corrimiento de la coma en el número original.
El caso de los números muy pequeños es exactamente igual, usando potencias de 10 con exponente negativo.
Ejemplos de Notación Científica:
| Medida de: | Nº escrito en notación decimal | Nº escrito en Notación científica |
| Masa de la Tierra | 5.983.000.000.000.000.000.000.000kg. | 5,983 · 1024 Kg |
| Diámetro del Sol | 1.391.000km. | 1,391 · 106km. |
| Tamaño de un microbio | 0,000004 cm. | 4 · 10-6 cm. |
| Tamaño de un virus | 0,00000002 cm. | 2 · 10-8 cm. |
| Tamaño de lo glóbulos Rojos | 0,0000075 mm. | 7,5 · 10-6 mm. |
| Tamaño de una bacteria | 0,0000002 mm. | 2 · 10-6 mm. |
| Diámetro del ADN | 0,0000000002 mm. | 2 · 10-9 mm. |
| Diámetro de un Protón | 0,000000000000001 mm. | 1 · 10-15 mm. |
| Masa de un Neutrón | 0,0000000000000000000000000017 mm. | 1,7 · 10-27 mm. |
| Neuronas que forman el Sistema Nervioso | 10.000.000.000 | 1 · 1010 |
| Velocidad de la Luz | 300.000.000m/s. | 3 · 108m/s. |
| Radio Ecuatorial de la Tierra | 6.370.000 m. | 6,37 · 106 m. |
| Peso de un Átomo de Plutonio | 0,0000000000000000000039 g. | 3,9 · 10-22g. |
| Diámetro de Júpiter | 144.000.000m. | 1,44 · 108m. |
| Distancia que recorre la luz en 1 hora | 108.000km. | 1,08 · 105km. |
| Distancia que recorre la luz en 1 día | 25.920.000km. | 2,592 · 107km. |
| Distancia que recorre la luz en 1 año | 946.080.000km. | 9,4608 · 108km. |
| Distancia de la Tierra a la estrella más cercana (Alfa Centauro) | 18.820.000.000.000.000.000km. | 1,882 · 1019km. |
| 1 año luz aprox. es : | 9.408.000.000.000km. | 9,408 · 1012km. |
| Distancia desde la Galaxia más cercana, visible desde el hemisferio sur(Gran nube de Magallanes) a la Tierra. | 1.611.600.000.000.000.000km. | 1,6116 · 1018km. |
| Cantidad de años desde la explosión del Big-Bang | 10.000.000.000 años | 1 · 1010 años |
| Medida del diámetro Universo antes del Big-Bang | 0,000000000000000000000000000000001cm. | 1 · 10-33cm. |
| Radio ecuatorial de Mercurio | 2.440.000m. | 2,44 · 106m. |
| Masa de Mercurio | 330.000.000.000.000.000.000.000kg. | 3,3 · 1023kg. |
| Distancia de Mercurio al Sol | 57.900.000.000m. | 5,79 · 1010m. |
| Radio ecuatorial de Venus | 6.050.000m. | 6,05 · 106m. |
| Masa de Venus | 4.870.000.000.000.000.000.000.000kg. | 4,87 · 1024kg. |
| Distancia de Venus al Sol | 108.000.000.000m. | 1,08 · 1011m. |
| Radio ecuatorial de Marte | 3.400.000m. | 3,40 · 106m. |
| Masa de Marte | 642.000.000.000.000.000.000.000kg. | 6,42 · 1023kg. |
| Distancia de Marte al Sol | 228.000.000.000m. | 2,28 · 1011m. |
| Radio ecuatorial de Júpiter | 71.500.000m. | 7,15 · 107m. |
| Masa de Júpiter | 1.900.000.000.000.000.000.000.000.000kg. | 1,9 · 1027kg. |
| Distancia de Júpiter al Sol | 778.000.000.000m. | 7,78 · 1011m. |
| Radio ecuatorial de Saturno | 60.300.000m. | 6,03 · 107m. |
| Masa de Saturno | 568.000.000.000.000.000.000.000.000kg. | 5,68 · 1026kg. |
| Distancia de Saturno al Sol | 1.430.000.000.000m. | 1,43 · 1012m. |
| Radio ecuatorial de Urano | 25.300.000m. | 2,53 · 107m. |
| Masa de Urano | 86.800.000.000.000.000.000.000.000kg. | 8,68 · 1025kg. |
| Distancia de Urano al Sol | 2.870.000.000.000m. | 2,87 · 1012m. |
| Radio ecuatorial de Neptuno | 24.800.000m. | 2,48 · 107m. |
| Masa de Neptuno | 102.000.000.000.000.000.000.000.000kg. | 1,02 ·1026kg. |
| Distancia de Neptuno al Sol | 4.500.000.000.000m. | 4,50 · 1012m. |
| Radio ecuatorial de Plutón | 1.160.000m. | 1,16 · 106m. |
| Masa de Plutón | 13.600.000.000.000.000.000.000kg. | 1,36 · 1022kg. |
| Distancia de Plutón al Sol | 5.910.000.000.000m. | 5,91 · 1012m. |
| Distancia de la Tierra al Sol | 149.600.000.000m. | 1,496 · 1011m. |
| Masa de la Luna | 73.600.000.000.000.000.000.000kg. | 7,36 · 1022kg. |
| Radio medio de la Luna | 1.740.000m. | 1,74 · 106m. |
| Masa del Sol | 1.991.000.000.000.000.000.000.000.000.000kg. | 1,991 · 1030kg. |
| Radio medio del Sol | 696.000.000m. | 6,96 · 108m. |
| Distancia promedio Tierra-Luna | 384.000.000m. | 3,84 · 108m. |
| Densidad del agua(20º C y 1atm) | 1.000kg/m3 | 1,00 · 103kg/m3 |
| Presión atmosférica estándar | 101.300Pa | 1,013 · 105Pa |
| Masa de un Electrón | 0,0000000000000000000000000000009109kg. | 9,109 · 10 -31 Kg |
Operatoria en Notación Científica:
Adición y Sustracción en N.C:
Si hay que sumar o restar medidas expresadas en Notación Científica (Mx10n). Si estas tienen el mismo exponente, simplemente suma o resta los valores de k, manteniendo el mismo valor que n.
EJEMPLOS
Cómo sumar y restar con exponentes iguales
4 x 108 m + 3 x 108 m = 7 x 108 m
4 x 10-8 m + 3 x 10-8 m = 7 x 10-8 m
8.1 x 106m - 4.2 x 106 m = 3.9 x 106 m
6.2 x 10-3 - 2.8 x 10-3 m = 3.4 x 10-3 m
Si las potencias de diez no son iguales, hay que hacerlas iguales antes de sumar o restar. Mueve el punto decimal hasta igualar los exponentes.
EJEMPLOS
Cómo restar y sumar con exponentes distintos
a. 4.0 x 106 m + 3 x 105 m c.4.0 x 10-6 Kg - 3 x 10-7 Kg
= 4.0 x 106 m + 0.3 x 106 m =4.0 x 10-6 Kg - 3 x 10-6 Kg
= 4.3 x 106 m =3.7 x 10-6 Kg
b. 4.0 x 106 cm - 3 x 105 cm
= 4.0 x 106 cm - 0.3 x 106 cm
= 3.7 x 106 cm
La multiplicación en la Notación Científica:
Las medidas expresadas en notación científica se pueden multiplicar sin importar si los exponentes son distintos o no. Multiplica los valores de K, luego suma los exponentes.
Ejemplo:
a. ( 3 · 106m) ( 2 · 103m) = 6 · 106+3 m2 = 6 · 109m2
b. ( 2 · 10-5m) ( 4 · 109m) = 8 · 109-5 m2 = 8 · 104 m2
c. (4 · 103kg) (5 · 1011m) = 20 · 103+11 kg. · m = 2 · 1015kg. · m
La división en la Notación Científica:
Las medidas expresadas en Notación Científica pueden dividirse, sin importar si los exponentes son distintos o no. Divide los valores de k y resta el exponente del divisor del exponente del dividendo.
Ejemplo:
a. 8 · 106m = 4 · 106-3m/s = 4 · 103m/s
2 · 103 s
b.8 · 106kg = 4 · 106-(-2) kg/m3 = 4 · 108kg/m3
2 · 10-2m3
CLASIFICACIÓN DE VECTORES
Elementos de un vector, descripción de cada uno.
El vector esta comprendido por los siguientes elementos:
-
La Dirección: esta determinada por la recta de soporte y puede ser vertical, horizontal e inclinada u oblicua.
-
La orientación: o sentido, esta determinada por la flecha y puede ser horizontal hacia la derecha o hacia la izquierda, vertical hacia arriba o hacia abajo e inclinada ascendente o descendente hacia la derecha o hacia la izquierda.
-
El punto de aplicación: esta determinado por el punto origen del segmento que forma el vector.
-
La longitud o módulo: es el número positivo que representa la longitud del vector.
PROBLEMAS DE VECTORES
Adición y sustracción de vectores, grafica y analíticamente; ejemplos.
La adición (y la sustracción) de dos matrices A + B (o A - B) requiere que las matrices sean de dimensiones iguales. A continuación cada elemento de una matriz se suma (o resta) del elemento correspondiente de la otra matriz. Así, a11 de A se sumara (o restara) a b11 de B; a12, a b12, etc.
Ejemplo.
A continuación se calcula la suma A + B, dadas las matrices A y B:

(3*3) 
(3*3) 
(3*3)= 
La diferencia C - D, dadas las matrices C y D, se determina como sigue:
(2*2) 
(2*2) 
(2*2)= 
-
Grafica: b
. a
a + b
-
Analíticamente:
Para sumar vectores de forma analítica debemos conocer sus coordenadas cartesianas. Si alguno de los vectores sumando está expresado en coordenadas polares debemos, en primer lugar, expresarlo en coordenadas cartesianas. La adición se realiza entonces sumando componente a componente. De esta forma, la suma de los vectores (2,3) y (-1,2) será el vector (1,5): (2,3)+(-1,2)=(2+[-1],3+5)=(1,5). La adición de vectores se convierte, en realidad, en una suma de pares de números.
SUMA DE VECTORES
La suma de vectores A y B se obtiene al hacer coincidir el extremo de uno de ellos con el origen del otro; la suma es el vector que va del inicio del primero al extremo del segundo.
Las propiedades de la suma de vectores son:
Propiedad conmutativa
![]()
![]()
Propiedad de la desigualdad del triángulo
![]()
Propiedad asociativa
La suma de vectores se puede realizar de dos formas, la primera es utilizando la ley de los senos y cosenos, la segunda forma es por medio de descomposición de fuerzas. Más adelante hay varios problemas aplicando lo antes dicho.
RESTA DE VECTORES.
Restar el vector B del vector A es equivalente a sumarle el inverso aditivo de B. Para restar vectores se unen en su origen y el vector resta es la unión de sus extremos dibujando el sentido hacia el que se le va a quitar, el paso siguiente es calcular el vector con el mismo procedimiento que en la suma.
A-B B-A
A B A B
multiplicación de un numero por un vector, grafica y analíticamente.
Los vectores libres se pueden multiplicar por un número real n. El vector resultante será un vector de módulo n veces el original, de la misma dirección que el original y de sentido igual al original si n es positivo y de sentido contrario si n es negativo.
Al vector A+A le llamamos 2A, observándose que el vector 2A es el doble de tamaño que el vector A y con su misma magnitud y sentido. Así multiplicar un vector A por un número real P es hacer PA P veces más largo que A.
Propiedad conmutativa.
Propiedad asociativa.
Propiedad distributiva.
Producto escalar de 2 vectores. Definición y ejercicios.
Los productos vectoriales son el producto punto o el producto cruz. El primero de ellos “Producto punto” es el siguiente:
El producto punto de dos vectores se define como el producto de sus magnitudes por el coseno del menor ángulo formado por ellos. En símbolos se representa:
Propiedad conmutativa
Propiedad asociativa
Propiedad distributiva
El producto cruz se define como el producto de sus magnitudes por el seno del ángulo formado por ellos en la dirección n. En símbolos se representa:
El producto cruz es anticonmutativo
Pero:
Propiedad distributiva
Siendo m un escalar
Otra propiedad sería:
Fuerzas en el espacio:
Las fórmulas que se utilizan para encontrar las componentes y sus ángulos directores son:
MECÁNICA DEL CUERPO SÓLIDO
EQUILIBRIO EN EL SÓLIDO RIGIDO LIBRE
Cualquiera ke sea el desplazamiento virtual del sólido libre es posible descomponerlo en dos: uno paralelo al eje y otro circular alrededor de este eje. Con respecto al movimiento paralelo al eje EE cada punto del sólido describirá un desplazamiento rectilíneo de igual longitud ke los demás y paralelo a ellos y al eje EE, siendo el valor del trabajo virtual para el sólido igual a: Tv = ds · F · cos y considerando la condición establecida para el equilibrio Tv = ds · F · cos = 0 lo ke ekivale a las componentes de F respecto a los ejes a: dx Xi + dy Yi + dz Zi = 0 En cuanto al desplazamiento virtual de rotación también debe ser distinto de cero, por lo ke tendrá en la expresión MEE · F ·DE debe ser MEE · F = 0 quedando como ecuaciones universales Xi = 0 Yi = 0 Zi = 0
MXX · F = (yi Zi -zi Yi) MYY · F = (zi Xi -xi Zi)
MZZ · F = (xi Yi -yi Xi)
Para que un sólido libre se encuentre en equilibrio es necesario, que las sumas algebraicas de las proyecciones de las fuerzas que sobre el están actuando sobre cada eje coordenado sean nulas y también lo sean la suma algebraica de los momentos de dichas fuerzas respecto de cada eje coordenado
EQULIBRIO DE UN SOLIDO CON UN PUNTO FIJO
Podemos suponer ke se trata de un solido libre en el ke se aplica en el punto O del mismo una fuerza cuyo efecto en el solido es el mismo que el producido por el enlace en el punto O. Llamaremos R a la resultante. Las fuerzas ke estan aplicadas sobre el solido y la reaccion R se encuentran en ekilibrio, por lo ke eleginos el punto O en el origen del sistema de coordenadas de forma ke las ecuaciones a cumplir son:
Rx + Xi = 0 Rv + Yi = 0 Rz + Zi = 0
Mx = 0 My = 0 Mz = 0
EQUILIBRIO DE UN SOLIDO CON UN EJE FIJO
La condicion necesaria para que un solido con un eje fijo no gire alrededor de el es que el momento resultante, respecto al eje fijo, de las fuerzas que sobre el actúan sea nulo. Sin embargo no es suficiente esta condicion puesto ke ademas ha de cumplirse que el solido no tenga movimiento de rotación uniforme. La fuerza aplicada sobre el solido puede ser descompuesta según tres direcciones: una dirección paralela al eje de rotación del solido, otra perpendicular al mismo eje y que le corta y una tercera normal al plano que determinan las dos componentes anteriores. A continuación hayamos las tres reacciones a las tres componentes, con lo ke tendremos ke su suma geométrica nos proporciona la reaccion total.
EQULIBRIO DE UN SOLIDO QUE SE APOYA SOBRE UN PLANO
Si el solido esta en ekilibrio, con sus cuatro puntos de apoyo en contacto con el plano, estando la resultante de esas cuatro reacciones aplicada en un plano interior de la base de sustentación. Debiendo esta resultante equilibrar a las fuerzas aplicadas al solido dichas fuerzas equivalen a una fuerza P, normal al plano de apoyo y que le cortara en un punto del interior de la base de apoyo F " f ·P
RAPIDEZ Y VELOCIDAD
Rapidez.- Movimiento acelerado o velocidad impetuoso.
Velocidad. Cualidad de un movimiento de efectuarse en un tiempo relativamente corto; cualidad del móvil que lo efectúa.
Velocidad (
Descargar
| Enviado por: | Dark |
| Idioma: | castellano |
| País: | México |
