Ingeniero en Electrónica
Filtros de ondas senoidales
PRACTICA 7
FILTROS
Un filtro es una red eléctrica usada para cambiar la amplitud y fase de una onda senoidal de una manera pres-crita.
El cambio depende de la frecuencia de la onda senoi-dal. Un filtro puede pasar ondas senoidales que están dentro de una banda de frecuencias y atenuar todas las que estén fuera de esa banda.
Generalmente un flitro se encuentra entre la excita-ción y la carga, como se muestra en la figura 7.1 donde la excitación Vi(t) y la salida Vo(t) están definidas por:
Vi(t)= Vmsen (wt + ðð ððð
Vo(t) =Vm M(w) sen (ðt + ð ð ð(ððð ððð
Donde:
M(w)= T(jw)
ð(jw)=T(s)
ð(ððð Es el argumento de de T(jw)
ðð Es el desfasamiento de la señal de excitación.
La entrada al filtro es una onda senoidal que puede tener un corrimiento en su fase, y la salida del filtro será una onda senoidal de la misma frecuencia afectada en magnitud por M(w) y en fase por fi.
Según el tipo de elementos que compongan la red eléctrica los filtros se clasifican en activos y pasivos.
Son filtros pasivos aquellos cuya red está formada por elementos resistivos (R,L,C) u sea puros elementos pasivos.
Los filtros pasivos se caracterizan por atenuar la señal de excitación. La ganancia máxima de estos filtros es siempre menor que la unidad y esto se debe a que la red no contiene elementos capaces de amplificar la señal de entrada. En cambio los filtros activos si son capaces de obtener a su salida señales amplificadas, o sea, mayores que uno, aunque la señal de salida puede también ser atenuada.
Según su respuesta a la frecuencia los filtros se clasifican de la siguiente manera:
-Paso bajo
-Paso alto
-Paso de banda
-Rechazo de banda
Esta clasificación es muy importante , ya que define el comportamiento d la respuesta a la frecuencia de la red, independientemente de los elementos que la compongan.
En la siguiente figura se muestran las gráficas idealizadas de la magnitud contra la frecuencia de los cuatro tipos de filtros enlistados arriba.
FILTRO PASA BAJO FILTRO PASA ALTO
FILTRO PASO BANDA FILTRO RECHAZOBANDA
Se le llama banda pasante a la región de frecuencia donde la señal en la salida no es atenuada a un valor menor de .7071 de su valor máximo, y se le llama banda atenuada a toda la región de frecuencia donde la señal en la salida es atenuada por debajo del valor señalado anteriormente.
FILTRO PASA BAJO DE PRIMER ORDEN
La función de transferencia de un filtro pasa bajo de primer orden está dada por la siguiente expresión:
T(s)= Howc
s+wc
donde Ho es el factor de ganancia
wc es la frecuencia de codo
La expresión anterior podemos escribirla de la siguiente manera
T(jw)= Howc = Ho
jw+wc jw/wc+1
De donde podemos obtener las expresiones en magnitud y la fase
T(jw) = M(w)= Ho
(1 + (w/wc)2 )1/2
ð(ððð ðtan-1 ðððc
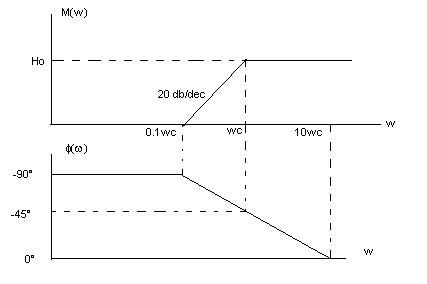
Podemos graficar las curvas correspondientes a la magnitud y la fase dando valores a w en las expresiones anteriores. Debido a que el efecto interesante ocurre al-rededor del punto donde se presenta la frecuencia de codo (wc) hacemos w igual a wc, a un décimo de wc y a diez veces wc .
Gráfica de la magnitud y la fase
De las gráficas anteriores deducimos que la banda pasante está com- prendida desde D.C hasta wc de maneratal que una señal de entrada cuya frecuencia este dentro de este rango será afectada por Ho. La banda atenuante se encuentra para cualquier valor de frecuencia mayor de wc, donde el grado de atenuación es de 20 db/dec. Este valor de atenuación ocurrirá siempre en funciones de primer orden.
Notamos también que en la banda pasante, para una señal próxima a wc la magnitud se evrá afectada por Ho pero la fase de la señal de salida respecto a la entrada estará próxima a -45 grados.
Si queremos que la señal de salida no se vea afectada en su fase debemos trabajar con señales de 0.1 wc.
FUNCION DE TRANSFERENCIA DE SEGUNDO ORDEN
La función de transferencia de un filtro de segundo orden pas bajo está definido de la expresión siguiente:
T(s)= Howc
S2 + sðcð ð ðc2
De donde
ðð .7071
2ðððððð
Podríamos ver que de esta ecuación si se graficará la magnitud, notaríamos que en la banda de rechazo la pendiente es de 40 db/dec y es mayor por lo que se acerca al filtro ideal.
Dado que la banda pasante está copmprendida desde D.C. hasta donde se presenta la frecuencia del codo del filtro wc, podemos aprovechar como ancho de banda pasante si en la frecuencia de codo pasa, la curva de respuesta por -3 db, por lo que el factor de amortiguamieto es igual a .7071.
FUNCION DE TRANSFERENCIA DE UN FILTRO PASO ALTO DE PRIMER ORDEN
La función de transferencia de un filtro paso alto de primer orden está dada por
T(s)= Hos
s+jw
T(jw)= Hojw/wc
jw/wc+1
De esta expresión podemos obtener las expresiones que definen a la magnitud y a la fase
M(jw) = How/wc
(1+(w/wc)2)1/2
ð(ððððððð tan-1 ðððc
Para un proceso análogo al desarrollado en los filtros paso bajo obrenemos las gráficas de la magnitud y de la fase para el filtro paso alto.
La función de transferencia de un filtro de segundo orden pasa alto está dada por:
T(s)= Hos2
s2 + 21/2wcs + wc2
sustituyendo s por jw y normalizanndo tenemos
T(jw)= Ho(jw/wc)2
1+ 21/2jw/wc - (w/wc)2
donde M(w) está dada por
M(w)= Ho(w/wc)1/2
( 1-(w/wc)2 + 2(w/wc)2)1/2
ð(ððð180°- tan-1 21/2w/wc/(1-(w/wc)2
FILTRO PASO DE BANDA
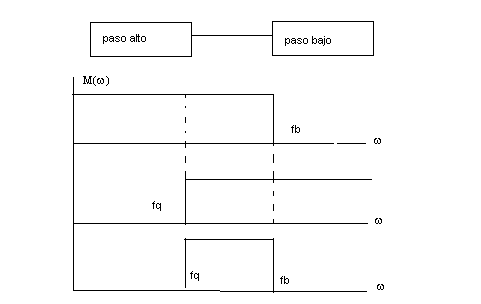
Se puede implementar un filtro paso de banda si conectamos en cascada un filtro paso alto con un paso bajo. El filtro paso alto se encarga de ate- nuar todas las bajas frecuencias que se encuentran debajo de su frecuencia de codo de tal manera que la salida de este filtro sea la excitación del paso bajo. Este filtro dejará pasar todas las señales mayores que la frecuencia de codo del filtro paso alto, y atenuará todas las frecuencias que sean mayores que su frecuencia de codo fb obteniéndose a la salida la banda de frecuencia comprendida en el intervalo.
Como podemos notarlo la frecuencia de codo del filtro paso bajo debe ser forzosamente mayor que la frecuencia de codo del filtro paso alto, ya que de no cumplirse esta condición, la señal en la salida aparecerá atenuada res-pecto de la entrada para cualquier valor de frecuencias de la señal de excitación.
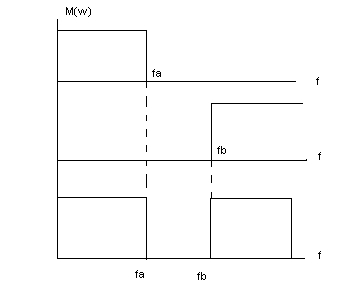
FILTRO RECHAZO DE BANDA
Para implementar un filtro rechazo de banda se puede utilizar como en el caso anterior, un filtro paso bajo y un filtro paso alto, pero ahora co- nectados en paralelo. Dado que los filtros están conectados a la misma excitación, las señales de baja frecuencia no serán afectadas por el filtro paso bajo pero sí serán atenuadas por el paso alto, y las señales de alta frecuencia no serán afectadas por el filtro pasa alto pero sí por el filtro paso bajo. La frecuencia de codo del filtro bajo deberá ser menor que la frecuencia de codo del paso alto, de otra manerano se podría generar el efecto del filtro rechazo de banda. Entre las frecuencias de codo fa y fb se presenta la banda de rechazo. En la figura se muestra el filtro rechazo de banda y su respuesta en magnitud:
Vo(t)
FILTRO
Vi(t)
-90°
-45°
10wc
wc
0.1wc
20 db/dec
20 db
Descargar
| Enviado por: | Joel Rivera |
| Idioma: | castellano |
| País: | México |
