Matemáticas
Factorización
Factorización
CARRERA: Profesorado en Matemática
AÑO:2004
INTEGRANTES:
Factorización
PLANIFICACIÓN DE LA CLASE
TEMA: “Cálculo de las raíces de un polinomio: Factorización”
Tener en cuenta que los alumnos ya saben ecuación de segundo grado y polinomios. Esta etapa es la culminación de Factoreo.
EJE: Álgebra y Geometría
CURSO: Primer Año de Polimodal
Factorización
CONOCIMIENTOS PREVIOS:
-
CONTENIDOS CONCEPTUALES
-
Polinomios
-
Ecuación de segundo grado
-
CONTENIDOS PROCEDIMENTALES
-
Utilización de la regla de Ruffini para dividir polinomios por (x-a)
-
Deducción de la fórmula resolvente de una ecuación de segundo grado.
-
Cálculo de raíces (reales) de una ecuación de segundo grado.
-
Factorización de polinomios de segundo grado (raíces reales)
Factorización
EXPECTATIVAS DE LOGRO:
Que los alumnos sean capaces de:
-
Distinguir cada caso de factoreo
-
Decidir de manera correcta y de la forma más eficiente, cuál es el caso de factoreo que deben aplicar; y que lo sepan aplicar.
-
Identificar si un polinomio es primo o compuesto
-
Justificar cada paso que realizan, cuando se encuentren frente a un ejercicio en el cual deban aplicar más de un caso de factoreo
Factorización
ORGANIZACIÓN DE LA CLASE
Como los alumnos, se supone, que ya vieron los casos de factoreo, nosotras nos limitaríamos simplemente a recordar como funcionaban estos casos, mediante un ejemplo, de esta manera, nuestro objetivo sería refrescar los conocimientos ya vistos, con el objeto de interiorizar a los alumnos en el tema y así poder lograr una completa aplicación de cada uno de ellos.
Nuestra meta es que los alumnos puedan comprender a fondo el tema, que puedan, frente a un polinomio , de una o más variables, saber por donde empezar, qué propiedad aplicar, y así poder lograr la factorización de un polinomio compuesto en un producto de polinomios primos. La idea es dejar esto muy claro, para que los alumnos no tengan demasiadas dudas cuando se enfrenten al ejercicio.
Nosotras desarrollaríamos una clase global e integradora, a partir de conocimientos ya vistos con anterioridad.
Nuestra intención sería explicar ejercicios, lo más completos posibles, en el pizarrón, luego dejaríamos ejercitación para que los alumnos realicen de tarea; y la corrección de los mismos se realizaría la clase siguiente en el pizarrón, pero en esta oportunidad haríamos que los alumnos pasen al frente y expliquen como resolvieron el ejercicio y qué propiedades aplicaron en cada uno de ellos.
De esta manera lograríamos que los alumnos participen de la clase, y además también puede surgir que para un mismo ejercicio haya alumnos que lo resolvieron de distinta manera, y ambos resultados son correctos.
Factorización
Recuerdo de los casos de factoreo, mediante un ejemplo de cada uno de ellos:
A continuación detallamos en qué consiste cada uno de los casos, pero sin embargo, en la clase no lo vamos a hacer, ya que con el ejemplo es suficiente para que los alumnos recuerden cada uno
-
FACTOR COMÚN
Procedimiento:
1° Paso: Buscamos el factor común (que debe ser el mayor posible)
2° Paso: Se expresa el polinomio dado como el producto del factor común por el polinomio que resulta de dividir el polinomio dado por el factor común.
Ejemplos:
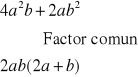
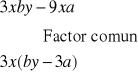
Factorización
-
FACTOR COMÚN POR GRUPOS
Se aplica en polinomios que no tienen factor común en todos sus términos.
Procedimiento
1° Paso: Se forman grupos de igual cantidad de términos que tengan factor común, se sustrae dicho factor común en cada uno de los grupos.
2° Paso: Debe quedar un paréntesis común.
3° Paso: Se extrae dicho paréntesis como factor común.
Ejemplos:
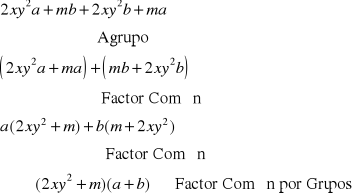

Factorización
-
TRINOMIO CUADRADO PERFECTO
Recuerdo: “Cuadrado de un Binomio”
![]()
Procedimiento:
1°Paso: Se reconocen los cuadrados perfectos, los cuales no deben tener un signo negativo adelante.
Y calculo sus raíces cuadradas, dichas raíces serán las bases.
2° Paso: Luego calculo el doble producto de sus bases; y luego nos fijamos si se verifica que el doble producto figura en el trinomio dado,
3° Paso: Si el doble producto figura en el trinomio dado, entonces decimos que es un Trinomio Cuadrado Perfecto; y luego lo factorizo como el cuadrado de un binomio, formado por dichas bases.
OBSERVACIONES MUY IMPORTANTES:
-
Si el doble producto que figura en el ”Trinomio dado” es positivo, entonces las bases del Cuadrado del Binomio tendrán las dos el mismo signo.
-
Si el doble producto que figura en el ”Trinomio dado” es negativo, entonces las bases del Cuadrado del Binomio tendrán signos opuestos.
Factorización
Ejemplos:
1)

2)

Factorización
-
CUATRINOMIO CUBO PERFECTO
Recuerdo: “Cubo de un Binomio”
![]()
Procedimiento:
1°Paso: Se reconocen los cubos perfectos
Y calculo sus raíces cúbicas, dichas raíces serán las bases.
2° Paso:
Luego calculo:
-
el triple producto del cuadrado de la primera base por la segunda
-
el triple producto de la primera base por el cuadrado de la segunda
Luego nos fijamos si estos cálculos figuran en el cuatrinomio dado,
3° Paso: Si estos cálculos figuran en el trinomio dado, entonces decimos que es un Cuatrinomio Cubo Perfecto; y luego lo factorizo como el cubo de un binomio, formado por dichas bases.
OBSERVACIÓN MUY IMPORTANTE:
Las bases que figuran en el Cubo del Binomio, van a conservar su signo.
Factorización
Ejemplos:
1)

2)

Factorización
-
DIFERENCIA DE CUADRADOS
Recuerdo: Producto de Binomios Conjugados
![]()
Procedimiento:
1° Paso: Debo identificar la resta (debe haber un solo signo negativo) y luego los cuadrados perfectos.
2° Paso: Calculo las bases de los cuadrados perfectos (haciendo la raíz cuadrada de cada uno)
3° Paso: Transformo la diferencia de cuadrados en un producto de binomios conjugados, formado por dichas bases.
Ejemplos:
1)

2)

Factorización
-
DIVISIBILIDAD
Este caso consiste en hallar los divisores del polinomio dado. Esto lo efectuamos mediante la siguiente propiedad.
“Si un número a es raíz de un polinomio P(x), dicho polinomio es divisible por (x-a), es decir que, al dividir P(x) por (x-a), el resto de la división es cero”
Por el teorema del resto tenemos que: P(a)=0
En símbolos:
P(x) (x-a)
-
C(x)
Cálculo de las raíces de un polinomio:
-
Para calcular la raíces de un polinomio en el cual figura una sola incógnita, elevada a una potencia, podemos calcular su raíz igualando a cero y resolviendo esa ecuación.
-
Cuando tenemos un polinomio de grado dos, donde aparece la incógnita dos veces (una elevada al cuadrado y otra con exponente 1, podemos calcular sus raíces aplicando la resolvente.
Factorización
En este caso hay que tener en cuenta que los alumnos ya saben factorizar un polinomio de este tipo.
Entonces:

-
Ahora si nos encontramos con un polinomio de grado mayor que dos, y la incógnita aparece más de una vez, podemos calcular sus raíces mediante el Teorema de Gauss, que si bien no nos asegura exactamente cuáles son sus raíces, nos da un número finito de raíces posibles.
Teorema de Gauss:
Este teorema nos parece conveniente explicarlo a través de un ejemplo, ya que el teorema enunciado en forma general nos parece demasiado complicado para que los alumnos puedan entenderlo.

Factorización

Entonces podemos escribir a P(x) como:
![]()
Factorización
Ejemplos:
1)

Factorización
2)

Factorización
COMBINACIÓN DE LOS CASOS DE FACTOREO
Ejercicio N° 1: Factoriza la siguiente expresión

Ejercicio N° 2: Factoriza la siguiente expresión

Factorización
Ejercicio N° 3: Factoriza la siguiente expresión

CÁLCULOS:

Factorización
Ejercicio N° 4: Factoriza la siguiente expresión
Una forma de resolverlo:

Factorización
Otra forma de resolverlo:

CÁLCULOS:

Factorización


Ejercicio N° 5: Factoriza la siguiente expresión

Factorización
CÁLCULOS:

Para recordar:
En el momento de factorizar una expresión debemos tener en cuenta que:
Primero nos fijamos si hay factor común en todos los términos, en caso de haber, lo extraemos.
Luego Consideramos la cantidad de términos:
-
Si hay dos términos puede ser que sea “Diferencia de Cuadrados” o puede ser que podamos utilizar el caso “Divisibilidad”.
-
Si hay tres términos puede ser “Trinomio Cuadrado Perfecto” o puede ser que podamos aplicar “Divisibilidad”
-
Si hay cuatro términos puede ser que sea un “Cuatrinomio Cubo Perfecto”, podemos intentar “Factor Común por Grupos” o utilizar “Divisibilidad”.
(Esto en realidad lo recordaríamos más o menos al finalizar o comenzar el primer ejercicio)
Factorización
Ejercitación
La siguiente ejercitación es para que los alumnos realicen de tarea y luego haríamos la corrección en el pizarrón, haríamos pasar a los alumnos para que los realicen, y así participar de la clase y poder marcarles lo errores en forma oral, para que todos escuchen y no vuelvan a cometer esos errores.
En el ejercicio N° 1 se puede aplicar
-
Factor Común por Grupos
-
Diferencia de Cuadrados
-
Divisibilidad
En el ejercicio N° 2 se puede aplicar
-
Factor Común
-
Factor Común por Grupos
-
Diferencia de Cuadrados
En el ejercicio N° 3 se puede aplicar
-
Factor Común
-
Cuatrinomio Cubo Perfecto
En el ejercicio N° 4 se puede aplicar
-
Factor Común
-
Trinomio Cuadrado Perfecto
En el ejercicio N° 5 se puede aplicar
-
Factor Común
-
Factor Común por Grupos
-
Divisibilidad
En el ejercicio N° 6 se puede aplicar
-
Factor Común
-
Factor Común por Grupos
-
Diferencia de Cuadrados
En el ejercicio N° 7 se puede aplicar
-
Factor Común
-
Diferencia de Cuadrados
Factorización
Factorizar los siguientes polinomios

Factorización
MODO DE EVALUACIÓN
En cuanto a la forma de evaluación del tema, la realizaríamos mediante un examen.
Dicho examen lo tomaríamos al finalizar el tema, dejando una clase intermedia, entre la última clase y el examen.
Con esta clase intermedia le daríamos a los alumnos la posibilidad de consultar sobre alguna inquietud que haya quedado sobre el tema dado. Claro que no le dedicaríamos una clase completa sino, algunos minutos o media hora, según las dudas que hayan surgido en los alumnos.
La evaluación o examen consistiría en la resolución de 5 ejercicios (ya que nos pareció la cantidad más apropiada), cuyos ejercicios estarían distribuidos de la siguiente manera:
El primer ejercicio para aplicar “Cuatrinomio Cubo Perfecto”
El segundo ejercicio para aplicar “Diferencia de Cuadrados”
El tercer, cuarto y quinto ejercicio para aplicar diversos casos de factoreo, en un mismo ejercicio, en general dos o tres casos en el mismo.
Factorización
MODELO DE EXÁMEN
Fecha: .........................................
Nombre y Apellido:......................................................................
Curso:..................................................
Factorizar hasta su mínima expresión, justificando cada paso que realices
Realizar todos los cálculos en la hoja.
![]()
![]()
![]()
![]()
![]()
Factorización
SOLUCIÓN DEL EXÁMEN
1) ![]()
Caso Aplicado: Cuatrinomio Cubo Perfecto

2) ![]()
Caso Aplicado: Diferencia de Cuadrados

Factorización
3) ![]()


Factorización
4)

5)

Factorización
6)
Factorización
Conclusión:
Bueno, entre las integrantes del grupo llegamos a la conclusión de que el tema que nos tocó exponer no fue el más apropiado para permitirnos lucirnos en ese momento. Más que la explicación de un tema es una clase práctica los alumnos ya conocen el tema, nosotras sólo nos limitamos a recordarles algo que ya habían visto y de esta manera poder realizar los ejercicios combinados (presentados en la clase).
Este es un tema que no permite vinculación con otros temas y tampoco podemos mediante el tema hacer que los alumnos puedan razonar los ejercicios; en este tema no podemos de ninguna forma plantear problemas que les permita a los alumnos utilizar otras herramientas, como puede ser la creatividad individual; es un tema que hay que darlo; (por supuesto que explicarlo lo más claro posible) y de ahí en más practicar para que los alumnos puedan aprenderlo.
Algunas integrantes del grupo consideramos que no es un tema “lindo” y otras consideramos que nos sirvió también a nosotras prepara la clase para refrescar también nosotras la memoria, además aprendimos cosas que nunca nos habían enseñado en la escuela secundaria.
Factorización
BIBLIOGRAFÍA UTILIZADA
-
ÁLGEBRA Y TRIGONOMETRÍA. Stanley A. Smith. Radall.I. Charles. John A. Dossey. Meruin L. Bihinger. Addison Wesley Logman
Red Federal de Formación Docente Continua. Ministerio de Cultura y Educación de la Nación.
-
MATEMÉTICA 1 ACTIVA. Puerto de Palos. Casa de Ediciones. Adriana Beño. Marialucita Colombo. Carina D´Albano. Oscar Scardella. Irene Zapica.
-
MATEMÁTICA 1. Susana N. Etchegoyen/ Enrique D. Fagale/ Silvia A. Rodríguez. Marta I. Auita de Kalan. María Rosario Alonso. Editorial Kapeluz.
32


Entonces: P(x)=(x-a)C(x)
Este tipo de división la podemos realizar con la Regla de Ruffini
Descargar
| Enviado por: | Nadia Soledad Aquino |
| Idioma: | castellano |
| País: | Argentina |
