Estadística
Estadística
1.1 INTRODUCCIÓN
La investigación cuya finalidad es: el análisis o experimentación de situaciones para el descubrimiento de nuevos hechos, la revisión o establecimiento de teorías y las aplicaciones prácticas de las mismas, se basa en los principios de Observación y Razonamiento y necesita en su carácter científico el análisis técnico de Datos para obtener de ellos información confiable y oportuna. Este análisis de Datos requiere de la Estadística como una de sus principales herramientas, por lo que los investigadores de profesión y las personas que de una y otra forma la realizan requieren además de los conocimientos especializados en su campo de actividades, del manejo eficiente de los conceptos, técnicas y procedimientos estadísticos
La estadística es la ciencia que estudia los métodos que permiten realizar este proceso para variables aleatorias. Estos métodos permiten resumir datos y acotar el papel de la casualidad (azar). Se divide en dos áreas:
estadistica descriptiva La descripción completa de una variable aleatoria está dada por su función densidad de probabilidad (fdp). Afortunadamente una gran cantidad de variables de muy diversos campos están adecuadamente descritas por unas pocas familias de fdps: binomial, Poisson, normal, gamma, etc. Dentro de cada familia, cada fdp está caracterizada por unos pocos parámetros, típicamente dos: media y varianza. Por tanto la descripción de una variable indicará la familia a que pertenece la fdp y los parámetros correspondientes.
estadistica inferencial. Los dos tipos de problemas que resuelven las técnicas estadísticas son: estimación y contraste de hipótesis. En ambos casos se trata de generalizar la información obtenida en una muestra a una población. Estas técnicas exigen que la muestra sea aleatoria. En la práctica rara vez se dispone de muestras aleatorias, por la tanto la situación habitual es la que se esquematiza en la figura
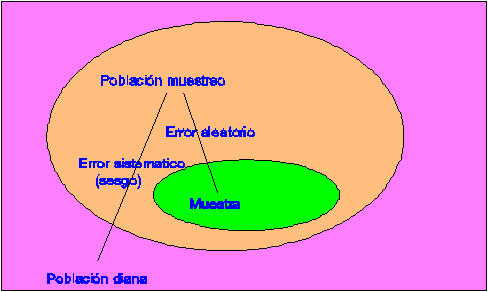
Entre la muestra con la que se trabaja y la población de interés, o población diana, aparece la denominada población de muestreo: población (la mayor parte de las veces no definida con precisión) de la cual nuestra muestra es una muestra aleatoria. En consecuencia la generalización está amenazada por dos posibles tipos de errores: error aleatorio que es el que las técnicas estadísticas permiten cuantificar y críticamente dependiente del tamaño muestral, pero también de la variabilidad de la variable a estudiar y el error sistemático que tiene que ver con la diferencia entre la población de muestreo y la población diana y que sólo puede ser controlado por el diseño del estudio.
1.2RECOPILACION DE DATOS
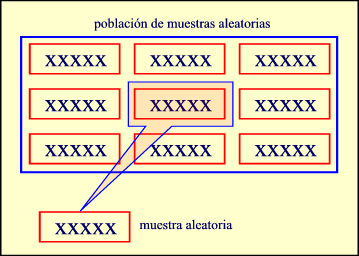
Poblacion y muestra Al recoger datos relativos a las características de un grupo de individuos u objetos, sean alturas y pesos de estudiantes de una universidad o tuercas defectuosas producidas en una fábrica, suele ser imposible o nada práctico observar todo el grupo, en especial si es muy grande. En vez de examinar el grupo entero, llamado población o universo, se examina una pequeña parte del grupo, llamada muestra. Una población puede ser finita o infinita. Por ejemplo, la población consistente en todas las tuercas producidas por una fábrica un cierto día es finita, mientras que la determinada por todos los posibles resultados (caras, cruces) de sucesivas tiradas de una moneda, es infinita. Si una muestra es representativa de una población, es posible inferir importantes conclusiones sobre las poblaciones a partir del análisis de la muestra. La fase de la estadística que trata con las condiciones bajo las cuales tal diferencia es válida se llama estadística inductiva o inferencia estadística. Ya que dicha inferencia no es del todo exacta, el lenguaje de las probabilidades aparecerá al establecer nuestras conclusiones. La parte de la estadística que sólo se ocupa de describir y analizar un grupo dado, sin sacar conclusiones sobre un grupo mayor, se llama estadística descriptiva o deductiva.
Muestra aleatoria: muestra elegida independientemente de todas las demás, con la misma probabilidad que cualquier otra y cuyos elementos están elegidos independientemente unos de otros y con la misma probabilidad.
1.4 ANÁLISIS DESCRIPTIVO DE LA INFORMACION :
ayudará a observar el comportamiento de la muestra en estudio, a través de tablas, gráficos..... Los resultados recogidos en la muestra se resumen en una matriz de datos N x M , en la cual N es el número de unidades de análisis utilizadas ( número de casos ) y M es el número de características de dichas unidades , unidades de las que tenemos información. Transformación de los datos : la transformación persigue la consecución de una distribución aproximada a la normal. Tipos de transformación :
Lineales : suma , resta , división , multiplicación , cambia los valores brutos ( datos obtenidos ) de la variable sin alterar nada mas.
No lineales monotónicas : cambian los valores originales y tambien sus distancias pero no el orden
No lineales no monotónicas : similar a la anterior pero no altera el orden..
1.4.1 DATOS NO AGRUPADOS
Tendencia central: la tendencia central se refiere al punto medio de una distribución. Las medidas de tendencia central se conocen como medidas de posición.
Dispersión: se refiere a la extensión de los datos en una distribución, es decir, al grado en que las observaciones se distribuyen.
1.4.2 DATOS AGRUPADOS
Medidas de Dispersión Se llaman medidas de dispersión aquellas que permiten retratar la distancia de los valores de la variable a un cierto valor central, o que permiten identificar la concentración de los datos en un cierto sector del recorrido de la variable. Se trata de coeficiente para variables cuantitativas.
Medidas de Tendencia central La estadística busca entre otras cosas, describir las características típicas de conjuntos de datos y, como hay varias formas de hacerlo, existen y se utilizan varios tipos de promedios. Se les llama medidas de tendencia central porque general mente la acumulación más alta de datos se encuentra en los valores intermedios.
Las medidas de tendencia central comúnmente empleadas son :
-
Media aritmética
-
Mediana
-
Moda
-
Media geométrica
-
Media armónica
-
Los cuantiaos
1.5 GRAFICOS DE ESTADISTICA DESCRIPTIVA
Los gráficos se han de explicar enteramente por sí mismos. El contenido de un gráfico deberá ser tan completo como sea posible. Las escalas vertical y horizontal estarán rotuladas con claridad dando las unidades pertinentes. La mayorías de los gráficos presentan información numérica con escalas, que deben rotularse para describir completamente la variable presentada en la escala y para variables de medida se dirán las unidades de medición. No se debe tratar de abarcar demasiada información en un solo gráfico. Es mejor hacer varios gráficos que comprimir toda la información en uno solo. Una regla práctica segura es evitar gráficos que contengan más de 3 curvas. Los gráficos tienen que dar una visión general y no una imagen detallada de un conjunto de datos. Las presentaciones detalladas se deben reservar para las tablas. Las tablas se explicarán por sí mismas enteramente. como los gráficos, se ha de dar suficiente información en el título y en los encabezamientos de columnas y filas de la tabla para permitir que el lector identifique fácilmente su contenido. Como el título será por lo general lo primero que se lee en detalle, deberá suministrar toda la información esencial sobre el contenido de la tabla y deberá especificar el tiempo, lugar, material ó estudio experimental y relaciones que se presenten en la tabla. Para cada variable numérica se han de dar las unidades. La función del rayado es dar claridad de interpretación. Las anotaciones de numéricas del cero se han de escribir explícitamente. Una anotación numérica no debe comenzar con una punto decimal. Los números que indican valores de la misma característica se han de dar con el mismo número de decimales.
PARA LOS SUIGUITES DATOS VAN A SER VASADOS EN LA TABLA 1(TANTO AGRUPADOS COMO NO AGRUPADOS)
| Tabla I. Distribución de frecuencias |
| Edad | Nº de pacientes |
| 18 | 1 |
| 19 | 3 |
| 20 | 4 |
| 21 | 7 |
| 22 | 5 |
| 23 | 8 |
| 24 | 10 |
| 25 | 8 |
| 26 | 9 |
| 27 | 6 |
| 28 | 6 |
| 29 | 4 |
| 30 | 3 |
| 31 | 4 |
| 32 | 5 |
| 33 | 3 |
| 34 | 2 |
| 35 | 3 |
| 36 | 1 |
| 37 | 2 |
| 38 | 3 |
| 39 | 1 |
| 41 | 1 |
| 42 | 1 |
1.5.1 NO AGRUPADOS
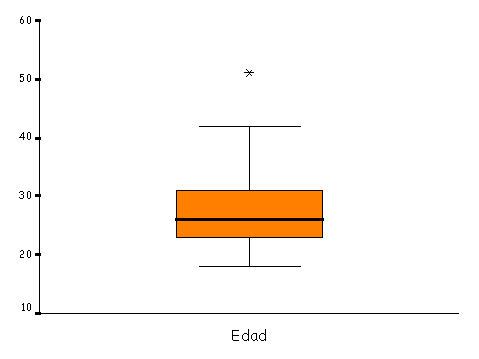
Otro modo habitual, y muy útil, de resumir una variable de tipo numérico es utilizando el concepto de percentiles, mediante diagramas de cajas. La Figura muestra un gráfico de cajas correspondiente a los datos de la Tabla I. La caja central indica el rango en el que se concentra el 50% central de los datos. Sus extremos son, por lo tanto, el 1er y 3er cuartil de la distribución. La línea central en la caja es la mediana. De este modo, si la variable es simétrica, dicha línea se encontrará en el centro de la caja. Los extremos de los "bigotes" que salen de la caja son los valores que delimitan el 95% central de los datos, aunque en ocasiones coinciden con los valores extremos de la distribución. Se suelen también representar aquellas observaciones que caen fuera de este rango (outliers o valores extremos). Esto resulta especialmente útil para comprobar, gráficamente, posibles errores en nuestros datos. En general, los diagramas de cajas resultan más apropiados para representar variables que presenten una gran desviación de la distribución normal.
1.5.2 DATOS AGRUPADOS
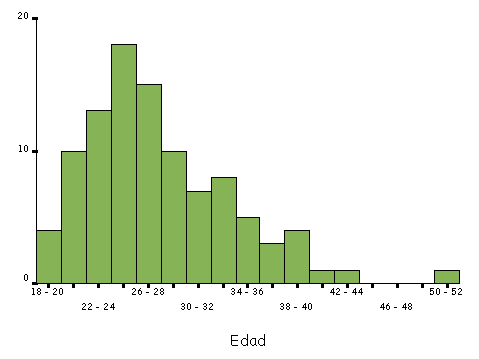
Histograma: Esta formado por rectángulos cuya base es la amplitud del intervalo y tiene la característica que la superficie que corresponde a las barras es representativa de la cantidad de casos o frecuencia de cada tramo de valores, puede construirse con clases que tienen el mismo tamaño o diferente ( intervalo variable). La utilización de los intervalos de amplitud variable se recomienda cuando en alguno de los intervalos , de amplitud constante, se presente la frecuencia cero o la frecuencia de alguno o algunos de los intervalos sea mucho mayor que la de los demás, logrando así que las observaciones se hallen mejor repartidas dentro del intervalo.
Ojivas: Cuando se trata de relacionar observaciones en un mismo aspecto para dos colectivos diferentes no es posible ejecutar comparaciones sobre la base de la frecuencia, es necesario tener una base estándar, la frecuencia relativa. La ojiva representa gráficamente la forma en que se acumulan los datos y permiten ver cuantas observaciones se hallan por arriba o debajo de ciertos valores. Es útil para obtener una medida de los cuartiles, deciles , percentiles.
Polígono de Frecuencias
Se puede obtener uniendo cada punto medio (marca de clase) de los rectángulos del histograma con líneas rectas, teniendo cuidado de agregar al inicio y al final marcas de clase adicionales, con el objeto de asegurar la igualdad del áreas.
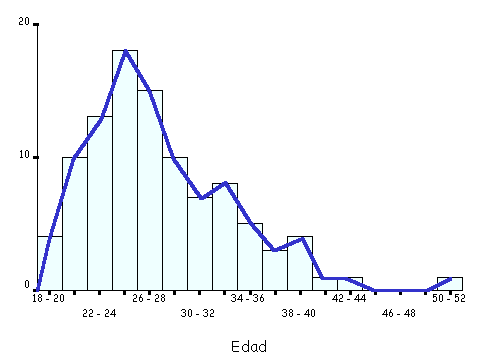
diagramas de barras son similares a los gráficos de sectores. Se representan tantas barras como categorías tiene la variable, de modo que la altura de cada una de ellas sea proporcional a la frecuencia o porcentaje de casos en cada clase . Estos mismos gráficos pueden utilizarse también para describir variables numéricas discretas que toman pocos valores
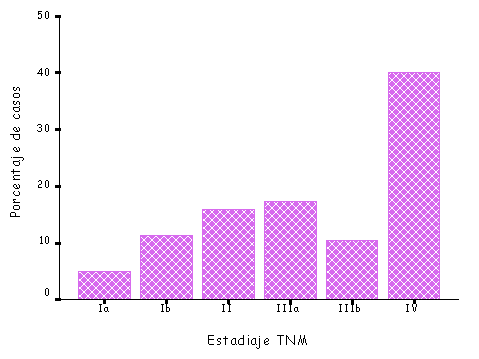
En los gráficos de sectores, también conocidos como diagramas de "tartas", se divide un círculo en tantas porciones como clases tenga la variable, de modo que a cada clase le corresponde un arco de círculo proporcional a su frecuencia absoluta o relativa. Un ejemplo se muestra en la . Como se puede observar, la información que se debe mostrar en cada sector hace referencia al número de casos dentro de cada categoría y al porcentaje del total que estos representan. Si el número de categorías es excesivamente grande, la imagen proporcionada por el gráfico de sectores no es lo suficientemente clara y por lo tanto la situación ideal es cuando hay alrededor de tres categorías. En este caso se pueden apreciar con claridad dichos subgrupos.
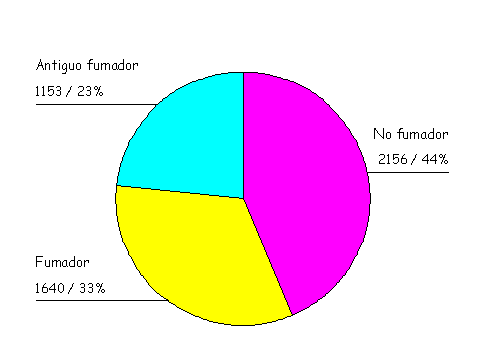
1.6 MEDIDAS DE ASIMETRIA Y APUNTAMIENTO
Sesgo: las curvas que representan los puntos de datos de un conjunto de datos pueden ser simétricas o sesgadas. Las curvas simétricas, tienen una forma tal que una línea vertical que pase por el punto más alto de la curva dividirá el área de ésta en dos partes iguales. Cada parte es una imagen espejo de la otra. En las curvas sesgadas, los valores de su distribución de frecuencias están concentrados en el extremo inferior o en el superior de la escala de medición del eje horizontal. Los valores no están igualmente distribuidos. Las curvas pueden estar sesgadas hacia la derecha (positivamente sesgadas) o sesgadas hacia la izquierda (negativamente sesgadas).
MEDIDAS DE CURTOSIS
Al comparar cuán aguda es una distribución en relación con la Distribución Normal, se pueden presentar diferentes grados de apuntalamiento.
1. Mesocúrtica, Normal
2. PlarticúrtiCa, Menor apuntalamiento
3. Leptocúrtica, Mayor apuntalamiento
Descargar
| Enviado por: | Chixho |
| Idioma: | castellano |
| País: | México |
