Matemáticas
Estadística
ESTADÍSTICA
DEFINICIONES
Población (universo o colectivo): Se denomina población al conjunto de todos los elementos que cumplen una determinada característica, que deseamos medir o estudiar.
Muestra: Se denomina muestra a cualquier subconjunto de la población.
Individuo (objeto): En estadística, se considera individuo a cada uno de los elementos de la población.
Carácter estadístico: Cada una de las propiedades (aspectos) que pueden estudiarse en los individuos de una población recibe el nombre de carácter estadístico.
-
Un carácter permite clasificar a los individuos de la población.
-
Un carácter puede ser cuantitativo si se puede medir.
-
Un carácter es cualitativo si no se puede medir (comparar).
El conjunto de valores que toma un carácter estadístico se llama variable estadística. Por tanto, dependiendo del carácter, una variable estadística puede ser cuantitativa o cualitativa.
Variable estadística discretas y continuas: Una variable estadística se llama discreta cuando sólo puede tomar determinados valores (con más precisión, cuando puede tomar un número finito o infinito numerable de valores).
La variable se llama continua cuando puede tomar todos los valores de un intervalo (valores tan próximos como se quiera).
Intervalos de clase: Se llama intervalo de clase a cada uno de los intervalos en que pueden agruparse los datos de una variable estadística.
Se definen para obtener una idea más concreta de la realidad. Si los valores de una variable se clasifican por intervalos, tal variable pasa a ser considerada continua.
El punto medio entre los extremos de cada intervalo se llama marca de clase.
Siempre que se agrupe una variable por intervalos se produce una pérdida de información, pues lo que se tiene en cuanta es la pertenencia o no de cada dato al intervalo y no su valor exacto.
Es importante tener en cuenta algunas consideraciones tanto al elegir la longitud de los intervalos como los extremos del primero y último. Entre ellas se destacan las siguientes:
-
Longitud del intervalo. Es conveniente que tengan la misma longitud.
-
Número total de intervalos. Dependerá de las características de la variable.
-
Elección de los extremos. Lo ideal es que no coincidan con ningún valor de la variable.
-
Marcas de clase. Si es posible se elegirán los intervalos de forma que las marcas de clase sean números enteros o con el menor números de cifras decimales posible.
Frecuencias: se llama frecuencia absoluta de un valor al número de veces que se repite éste.
Se denomina frecuencia absoluta acumulada de un valor a la suma de todas las frecuencias absolutas de los valores menores o iguales al considerado.
Acumular frecuencias carece de sentido cuando las variables son cualitativas.
Se designa con el término de frecuencia relativa de un valor a la suma de todas las frecuencias relativas de los valores menores o iguales al considerado.
Se llama frecuencia relativa acumulada de un valor a la suma de todas las frecuencias relativas de los valores menores o iguales al considerado.
Si cada frecuencia relativa se multiplica por 100 se obtiene el tanto por ciento correspondiente a cada valor.
Si tenemos definidos intervalos de clase, las frecuencias se miden en cada intervalo como el número de elementos que pertenecen al mismo.
En todos los casos, la suma de las frecuencias absolutas debe ser igual a la unidad, y la de los porcentajes deberá ser 100.
TIPOS DE GRÁFICOS
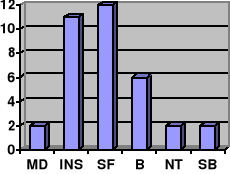
Diagrama de barras: recibe el nombre de diagrama de barras el gráfico que asocia a cada valor de la variable una barra, generalmente vertical, proporcional a la frecuencia (o a la cantidad) con que se presenta.
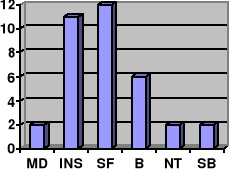
Ej.: La s notas de matemáticas de los 35 alumnos de una clase vienen dadas por la siguiente tabla:
| Calificaciones | MD | INS | SF | B | NT | SB | Total |
| Número de alumnos | 2 | 11 | 12 | 6 | 2 | 2 | 35 |
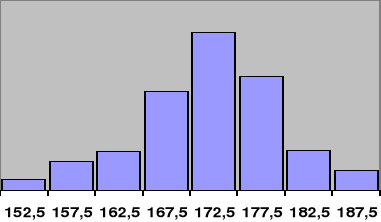
Histogramas: Son diagramas de barras que se utilizan específicamente para variables agrupadas por intervalo. Estos gráficos asocian a cada intervalo un rectángulo de superficie proporcional a la frecuencia correspondiente a dicho intervalo.
| Intervalo | M.C. |
| 150-155 | 152.5 |
| 155-160 | 157.5 |
| 160-165 | 162.5 |
| 165-170 | 167.5 |
| 170-175 | 172.5 |
| 175-180 | 177.5 |
| 180-185 | 182.5 |
| 185-190 | 187.5 |
Polígono de frecuencias: se considera polígono de frecuencias a la línea que une los puntos correspondientes a las frecuencias de cada valor o de los extremos superiores de las barras.
| Edad | Peso | Medición |
| 15 semanas | 120 g | 17 cm |
| 16 semanas | 200 g | 24 cm |
| 17 semanas | 300 g | 26 cm |
| 18 semanas | 400 g | 28 cm |
| 19 semanas | 500 g | 30 cm |
| 20 semanas | 650 g | 32 cm |
| 21 semanas | 750 g | 34 cm |
| 22 semanas | 890 g | 36 cm |
| 23 semanas | 1 Kg | 37 cm |
| 24 semanas | 1 Kg 200 g | 39 cm |
| 25 semanas | 1 Kg 300 g | 40 cm |
Descargar
| Enviado por: | Ana Arroba |
| Idioma: | castellano |
| País: | España |
