Ingeniero en Electrónica
Electrónica digital: Sistemas numéricos posicionales
1.1. Sistemas Numéricos Posicionales
En el sistema de números decimales se dice que la base o raíz es 10 debido a que usa 10 dígitos, y los coeficientes se multiplican por potencias de 10.
El sistema binario únicamente posee dos valores posibles que son 0 y 1, en los cuales cada coeficiente AJ se multiplica por 2J, como ejemplo tendremos el desarrollo del número binario 11010.11 el cual será representado por la siguiente manera :
1*24+1*23+0*22+1*21+0*20+1*2-1+1*2-2
16+8+0+2+0+0.5+0.25 = 26.75
Por lo tanto tenemos que un número en un sistema de base(r) tiene coeficientes multiplicados por potencias de (r) y quedaría representado de la siguiente manera :
an*rn+ an*rn+ . . . + a2*r2+ a1*r1+ a0*r0+ a-1*r-1+ . . . + a-m*r-m
1.2. Conversiones entre Sistemas Numéricos
Un número binario x puede convertirse en decimal efectuando la suma de las potencias cuyo valor es uno.
Ejemplo :
(1010.011)2 = 1*23+0*22+1*21+0*20+0*2-1+1*2-2+1*2-3
= 8+0+2+0+0+0.25+0.125
= 10.375
Para los números expresados en base r podríamos efectuar su conversión a decimal multiplicando cada coeficiente por la potencia correspondiente de r y sumando.
Ejemplo :
(630.4)8 = 6*82+3*81+0*80+4*8-1
= 384+24+0.5 = 408.5
Cuando deseamos efectuar la conversión de decimal a binario o ha cualquier otro sistema con base r es mas conveniente si el número se separa en parte entera y en una parte fraccionaria, y la conversión de cada parte se efectúa por separado :
Ejemplo :
Convertir el numero (41)10 a binario
41 1 LSB
20 0
10 0
5 1
2 0
1 1 MSB
(41)10 = (101001)2
Para convertir cualquier entero decimal han cualquier sistema de base r la división se hace entre r en lugar de 2.
Ejemplo :
Convertir el numero (153)10 a base 8
153 1 LSB
198 3
2 2 MSB
(153)10=(231)8
Para convertir una fracción decimal a binario, el sistema que se sigue es similar al que utilizamos para los enteros, sin embargo, se usa la multiplicación en lugar de la división, y los enteros se acumulan en lugar de los residuos.
Ejemplo :
convertir (0.6875)10 a base 2
Entero Fracción Coeficiente
0.6875 *2 1 0.3750 a-1 = 1
0.3750 *2 0 0.75a-2 = 0
0.75 *2 1 0.5a-3 = 1
0.5 *2 1 0.0a-4 = 1
(0.6875)10=(0.1011)2
Cuando deseamos convertir una fracción decimal en número expresado en base r, el procedimiento es similar, la multiplicación se hace con r en lugar de 2 y los coeficientes se encuentran con los enteros.
Ejemplo :
convertir (0.513)10 a base 8
Entero Fracción Coeficiente
0.513 * 8 4 0.104 a-1 = 4
0.104 * 8 0 0.832 a-2 = 0
0.832 * 8 6 0.656 a-3 = 6
0.656 * 8 5 0.248 a-4 = 5
0.248 * 8 1 0.984 a-5 = 1
0.984 * 8 7 0.872 a-6 = 7
Cuando deseamos hacer la conversión de un número decimal de una parte entera y una parte fraccionaria la conversión se hace por separado y posteriormente se combinan las dos respuestas.
Ejemplo :
(41.6875)10 -> (101001.1011)2
Números octales y hexadecimales.
Las conversiones entre código binario, octal y hexadecimal es muy importante en las comparaciones digitales, ya que cada dígito octal corresponde a tres dígitos binarios y a cada dígito hexadecimal corresponde cuatro dígitos binarios.
(10110001101011.111100000110)2 -> (26153.7406)8
Cuando deseamos convertir un número binario a hexadecimal, el proceso es similar excepto que el número binario se divide en grupos de 4.
(10110001101011.11110010)2 -> (2C6B.F2)16
La conversión a hexadecimal en binario se realiza con un procedimiento inverso al anterior esto es ; cada dígito octal se convierte en su equivalente binario de tres dígitos y cada dígito hexadecimal se convierte en su equivalente binario de cuatro dígitos.
Ejemplo :
(613.124)8 -> (110001011.001010100)2
(306.D)16 ->(001100000110.1101)2
Los números binarios son difíciles de manejar ya que se requiere dos o cuatro veces mas dígitos que su equivalente decimal.
Ejemplo :
(111111111111)2 -> (4095)10
Una forma de reducir esta deficiencia es emplear la relación entre el sistema de números binarios con el sistema octal o hexadecimal.
El número binario (111111111111)2 tiene 12 dígitos y los podemos expresar en octal (7777)8 (cuatro dígitos) o en hexadecimal como (FFF)16 (tres dígitos), la representación octal o hexadecimal es mas deseable ya que se representa en forma mas compacta, como un tercio o un cuarto del número de dígitos requeridos por el número binario equivalente.
1.3. Operaciones en Sistemas Numéricos
Complementos.
Este tipo de operación se utilizan en las computadoras digitales para simplificar la operación de sustracción y para manipulaciones lógicas.
Existen 2 tipos de complementos :
a) El complemento de r.
b) El complemento de r-1.
a)El complemento de r.
El complemento de r de un número positivo N en base r con una parte entera de n dígitos, será definido como el complemento de r a n y se define como rn-N;
Obtener el complemento de 10 de (52520)10
105-52520=47480
Obtener el complemento de 10 de (0.3267)10
100-0.3267=0.6733
Obtener el complemento de 10 de (25.639)10
102-25.639=74.361
Ejemplo : Obtener el complemento de 2 de (101100)2
26-(101100)2 = (100000)2-(101100)2=(0.1010)2
Por lo tanto tendremos que el complemento de 10 de un número decimal se puede formar dejando todos los ceros significativos sin cambios se resta el primer dígito del cero menos significativo de 10 y, entonces se restan todos los pocos dígitos menos significativos menores de 9.
El complemento de 2 puede formarse dejando todos los ceros menos significativos y el primer dígito diferente de 0 sin cambio, entonces se reemplazan los 1 por 0 y los 0 por 1 en los otros dígitos mas significativos.
b)Complemento de r-1.
Para un número positivo N en base r con una parte entera de n dígitos y una parte fraccionaria de n dígitos y una parte fraccionaria de m dígitos, el complemento de r-1 de m se define como rn-r-m-N.
Ejemplos :
Obtener el complemento de 9 de (52520)10
105-100-52520=47479
Obtener el complemento de 9 de (0.3267)10
100-10-4-0.3267=0.6732
Obtener el complemento de 9 de (25.639)10
102-10-3-25.639=74.36
Obtener el complemento de 1 de (101100)2
26-20-101100=10011
Obtener el complemento de 1 de (0.0110)2
20-2-4-0.0110=
Por lo tanto deducimos que :
El complemento de 9 de un número decimal se forma simplemente al restar cada dígito de 9. Y el complemento de 1 de un número binario es mas simple, ya que solo consiste en cambiar los 1 por 0 y los 0 por 1. Puesto que el complemento de r-1 es fácil de obtener, algunas veces es conveniente usarlo cuando se desea el complemento de r.
Sustracción con complemento de r.
La sustracción de 2 números positivos (M-N), ambos en base r, puede hacerse como sigue :
1.- Agréguese el minuendo m al complemento de r del sustraendo n.
2.- Verifique el resultado que se obtuvo en el paso 1 para el caso que exista un acarreo final.
a) Si existe un acarreo final, descártese.
b) Si no existe un acarreo final, tómese el complemento de r de número que se obtuvo en el paso 1 y colóquese un signo negativo en frente.
Ejemplo :
Utilizando el complemento 10 reste 72532-03250
complemento 10 de 03250=96750
72532-96750=69282
como no existe acarreo final se utiliza el paso b).
complemento 10 de 69282=27468
03250-27468=30718
complemento 10 de 30718=69282
resultado -69282
Utilizando el complemento 2 realice M-N con los números binarios dados.
M=1010100
N=1000100
complemento de N = 0111100
0111100
1010100
-----------
1 0010000
1011
1110
------
0101
1011
0001
------
1100
Resultado = -0011
Sustracción con complemento (r-1).
El procedimiento para esta operación es exactamente el mismo que para el complemento a r excepto por una variación llamada acarreo final. Para la resta de M-N en base r puede calcularse tomando en cuenta los siguientes puntos :
1.- Agréguese el minuendo M al complemento de (r-1) del sustraendo N.
2.- Verifique el resultado que se obtuvo en el paso 1 para un acarreo final.
a) Si ocurre un acarreo final agréguese uno al dígito menos significativo (acarreo final desplazado).
b) Si no ocurre un acarreo final tómese el complemento de (r-1) del número obtenido en le paso 1 y colóquese al frente un signo negativo.
Ejemplo :
Realice el complemento de r-1 de M-N, M=72532 y N=03250
complemento 9 de N = 96749
72532
96749
--------
1 69281
como existe un acarreo final se realiza el paso a)
69281+1=69282
Realice el complemento de r-1 de M-N, N=03250 y M=72532
complemento 9 de N = 72532
03250
27467
---------
30717
como no existe acarreo final se realiza el paso b)
complemento 9 de 30717=69282
Resultado -69282
Ejemplo :
Obtener M-N para los siguiente valores, M=1010100 y N=1000100
complemento 1 de 1000100 = 0111011
1010100
0111011
-----------
1 0001111
como existe un acarreo final se realiza el paso a)
0001111
1
----------
0010000
1.4. Representación de Números Negativos
Debido a que muchas computadoras y calculadoras digitales manejan números negativos y positivos, se necesita algún medio de representación para el signo del número (+/-). Esto se lleva a cabo en general agregando otro bit al número, denominado bit del signo.
En términos generales la convención común que se a adoptado es que un cero en el bit del signo representa un número positivo y un uno, representa un número negativo.
Ejemplo :
El registro A contiene los bits 0110100, el contenido cero en el bit de mas a la izquierda (A6) es el bit del signo que representa al signo (+). Los otros seis bits son la magnitud del número, que es igual a 5210.
A6 A5 A4 A3 A2 A1 A0
0 1 1 0 1 0 0
0 110100
(+) Magnitud del numero
De este modo el número almacenado en el registro A es +52. El bit del signo se usa para indicar si un número binario almacenado es positivo o bien negativo. Para los números positivos, el resto de los bits se utilizan siempre para representar la magnitud del numero en forma binaria.
Para los números negativos, no obstante, existen tres formas posibles de representar la magnitud.
-
Forma de magnitud verdadera.
-
Forma de complemento a 1
-
Forma de complemento a 2
Forma de magnitud verdadera.
El ejemplo visto anteriormente, contiene un bit de signo y seis bits de magnitud. Los bits de magnitud son el equivalente binario verdadero de los valores binarios que se representan.
Aunque este sistema de magnitud verdadera es directo y fácil de entender, no es de tanta utilidad como los otros dos sistemas para representar números binarios con signo.
Forma de complemento a 1.
La forma de complemento a 1 de un número binario cualquiera se obtiene simplemente cambiando cada cero del número por 1 y cada uno por cero.
Ejemplo :
El complemento de 1 del número 101101 es 010010
Cuando se quiere representar números negativos en forma de complemento 1 el bit de signo se convierte en 1 y la magnitud se transforma de forma binaria verdadera.
-57 = 1 111001 (forma de magnitud real)
= 1 000110 (forma de complemento a 1)
NOTA : Observe que el bit de signo no se complementa sino que se conserva en un 1 a fin de indicar un número negativo.
Forma de complemento 2.
La forma de complemento 2 de un número binario se forma simplemente tomando el complemento 1 del número y sumando 1 a la posición del bit menos significativo.
Ejemplo :
convertir 111001 a su forma de complemento 2.
000110
1
---------
000111
De tal forma que -57 se escribirá como 1 000111 en su representación de complemento a 2.
Ejemplo :
Tres sistemas para representar números binarios con signo se muestran a continuación.
Sistema de magnitud verdadera Sistema de complemento 1 Sistema de complemento 2
+57 0 111001 0 111001 0 111001
-57 1 111001 1 000110 1 000111
NOTA : Un número positivo en cualquier representación tiene un cero en el bit de la extrema izquierda para un (+), seguido de un número positivo. Un número negativo siempre tiene un uno en el bit de la extrema izquierda para un (-),pero los bits de magnitud se representan de una forma diferente.
En la representación de signo-magnitud, estos bits son el número positivo ; en la representación de complemento de 1, estos bits son el complemento del número binario y en la representación de complemento 2, el número esta en su forma de complemento 2.
1.5. Suma y Resta en Complemento a Dos
El complemento 1 y 2 son muy semejantes pero el complemento 2 generalmente es mas usado debido a las ventajas que representa al aplicarse en circuitos.
Ejemplo : La suma de 2 números positivos +9 y +4
+9 01001 consumando
+4 00100 sumando
--- -------- -------------
+13 01101 suma = +13
NOTA : Los bits de signo del consumando y el sumando ambos son cero y pos lo tanto el bit del signo de la suma es cero, lo cual indica que la suma es positiva. Nótese que el consumando y el sumando se forman con el mismo número de bits, esto siempre debe llevarse a cabo en el sistema de complemento 2.
Ejemplo: Un número positivo y un número negativo menor.
+9 01001
-4 11100
--- ----------
+5 1 00101
Este acarreo se desprecia de manera que el resultado es 00101 (+5)
NOTA : En este caso el bit del signo del sumando es uno. Observe que el bit del signo (+) también participa en el proceso de adición, de hecho, se genera un corrimiento en la última posición de la suma, este corrimiento siempre es despreciado, de modo que la suma final es 00101 = (+5).
Ejemplo:Un número positivo y un numero negativo mayor.
-9 1 0111
+4 0 0100
--- --------
-5 1 1011
Se le saca el complemento 2
0100
1
------
0101
Se le agrega el bit de signo 10101 (-5).
NOTA: La suma en este caso tiene un bit de signo 1, lo cual indica que es negativo, esta se encuentra en su forma de complemento 2 de manera que los últimos 4 bits (1011), representan en realidad el complemento 2 de la suma.
Para determinar la magnitud verdadera de la suma, debemos de tomar el complemento 2 de 1011, el resultado será 0101(5).
Ejemplo:2 números negativos -9 y -4.
-9 1 0111
-4 1 1100
---- ---------
-13 1 1 0011
Se toma el complemento 2
Resultado:1 1101
Este resultado final vuelve a ser negativo y esta en forma de complemento 2 con un bit de signo 1. Nótese que 0011 es el complemento 2 de 1101(+13).
Ejemplo:2 números iguales y opuestos.
- 9 1 0111
+9 0 1001
--- ---------
0 1 0 0000
Sustracción con complementos a 2.
Esta operación en realidad comprende la operación de adición que hace uso del sistema de complemento 2.
Cuando se resta un número binario (el sustraendo) de otro número binario (el minuendo), el procedimiento es como sigue :
1.- Tómese el complemento 2 del sustraendo, incluye el bit del signo. Si el sustraendo es un número positivo, este se transforma en un número negativo en forma de complemento 2. Si el sustraendo es un número negativo, este se convertirá en uno positivo en forma binaria verdadera. En otras palabras se altera el signo del sustraendo.
2.- Después de formar el complemento 2 del sustraendo este se suma al minuendo. El minuendo se conserva en su forma original. El resultado de esta adición representa la diferencia que se pide. El bit del signo de esta diferencia determina si es positivo o bien negativo, y si esta en forma binaria verdadera o en forma de complemento 2.
3 :- Recuérdese que ambos números deben tener el mismo número de bits.
Ejemplo:
+9 01001
- +4 11100
--- ---------
+5 1 00101
1.6. Codigos: Númericos y Alfanumericos
Tipos de Códigos
- Códigos Decimales
Los códigos binarios para dígitos decimales requieren un mínimo de cuatro bits. Se obtiene numerosos códigos diferentes al ordenar cuatro o mas bits en diez distintas combinaciones.
- Códigos de Detección de Error
La información binaria, se trata de señales de pulso modulado o bien, entrada o salida digital a computadora, puede transmitirse a trabes de alguna forma de medio de comunicación, como alambres u ondas de radio. Cualquier ruido externo que se introduce en un medio de comunicación física cambia los valores de bits de 0 a 1 y viceversa.
- Código Reflejado
Los sistemas digitales pueden diseñarse para procesar datos solo en una forma discreta. Muchos sistemas físicos suministran salida de información continua. Esta información puede convertirse en forma digital o discreta antes de que se aplique a un sistema digital. La información continua o analógica se convierte en forma digital mediante un convertidor de analógico a digital.
- Códigos Alfanuméricos
Muchas de las aplicaciones de las computadoras digitales requieren la manipulación de datos que constan no solo de números, sino también de letras. Por ejemplo, una compañía de seguros con millones de tenedores de póliza debe usar una computadora digital para procesar sus archivos. Para representar el nombre del tenedor de póliza en forma binaria, es necesario tener un código binario para el alfabeto. Además, el mismo código binario debe representar números decimales y algunos otros caracteres especiales. Un código alfanumérico (algunas veces abreviado álfame rico) es un código binario de un grupo de elementos que consta de diez dígitos decimales, las 26 letras del alfabeto y cierto numero de símbolos especiales como $. El numero total de elementos en un grupo alfanumérico es mayor de 36. Por lo tanto, debe codificarse con un mínimo de 6 bits (26=64, pero 25=32 no es suficiente).
Códigos Numéricos
Digito Decimal 8421(BCD) Exceso -3 84-2-1 2421 5043210(Biquinario)
0 0000 0011 00 0 0 0000 0100001
1 0001 0100 01 1 1 0001 0100010
2 0010 0101 01 1 0 0010 0100100
3 0011 0110 01 0 1 0011 0101000
4 0100 0111 01 0 0 0100 0110000
5 0101 1000 10 1 1 1011 1000001
6 0110 1001 10 1 0 1100 1000010
7 0111 1010 10 0 1 1101 1000100
8 1000 1011 10 0 0 1110 1001000
9 1001 1100 11 1 1 1111 1010000
Código reflejado de cuatro bits
(Código Gray)
Código Reflejado Decimal
0000 0
0001 1
0010 2
0011 3
0110 4
0111 5
0101 6
0100 7
1100 8
1101 9
1111 10
1110 11
1010 12
1011 13
1001 14
1000 15
Códigos Alfanuméricos
Carácter Código interno Código ASCII Código EBCDIC Código de tarjeta
6 - bits 7 - bits 8 - bits 12 - bits
A 010 001 100 0001 1100 0001 12,1
B 010 010 100 0010 1100 0010 12,2
C 010 011 100 0011 1100 0011 12,3
D 010 100 100 0100 1100 0100 12,4
E 010 101 100 0101 1100 0101 12,5
F 010 110 100 0110 1100 0110 12,6
G 010 111 100 0111 1100 0111 12,7
H 011 000 100 1000 1100 1000 12,8
I 011 001 100 1001 1100 1001 12,9
J 100 001 100 1010 1101 0001 11,1
K 100 010 100 1011 1101 0010 11,2
L 100 011 100 1100 1101 0011 11,3
M 100 100 100 1101 1101 0100 11,4
N 100 101 100 1110 1101 0101 11,5
O 100 110 100 1111 1101 0110 11,6
P 100 111 101 0000 1101 0111 11,7
Q 101 000 101 0001 1101 1000 11,8
R 101 001 101 0010 1101 1001 11,9
S 110 010 101 0011 1110 0001 0,2
T 110 011 101 0100 1110 0010 0,3
U 110 100 101 0101 1110 0011 0,4
V 110 101 101 0110 1110 0100 0,5
W 110 110 101 0111 1110 0101 0,6
X 110 111 101 1000 1110 0111 0,7
Y 111 000 101 1001 1110 1000 0,8
Z 111 001 101 1010 1110 1001 0,9
0 000 000 011 0000 1111 0000 0
1 000 001 011 0001 1111 0001 1
2 000 010 011 0010 1111 0010 2
3 000 011 011 0011 1111 0011 3
4 000 100 011 0100 1111 0100 4
5 000 101 011 0101 1111 0101 5
6 000 110 011 0110 1111 0110 6
7 000 111 011 0111 1111 0111 7
8 001 000 011 1000 1111 1000 8
9 001 001 011 1001 1111 1001 9
espacio 110 000 010 0000 0100 0000 no perforado
. 011 011 010 1110 0100 1011 12,8,3
( 111 100 010 1000 0100 1101 12,8,5
+ 010 000 010 1011 0100 1110 12,8,6
$ 101 011 010 0100 0101 1011 11,8,3
* 101 100 010 1010 0101 1100 11,8,4
) 011 100 010 1001 0101 1101 11,8,5
- 100 000 010 1101 0110 0000 11
/ 110 001 010 1111 0110 0001 0,1
, 111 011 010 1100 0110 1011 0,8,3
= 001 011 010 1101 0111 1110 8,6
2.1. Teoremas y Postulados del Álgebra de Boole (Postulados D'MORGAN)
Propiedades del álgebra de Boole.
1. Propiedad de cierre.
Para un conjunto s se dice que es cerrado para un operador binario si para cada elemento de S el operador binario especifica una regla para obtener un elemento único de S.
Para el conjunto N = {1,2,3,4,…} es cerrado con respecto al operador binario (+) por las reglas de la adición aritmética, ya que para que cualquier elemento a,b pertenecientes a N por la operación a + b = c el conjunto de los números naturales no esta cerrado con respecto al operador binario (-) por la regla de la resta aritmética, debido a que 2-3 = -1 y 2,3 pertenecen a N pero -1 no pertenece a N.
2. Ley asociativa.
El operador binario (*) es un conjunto S es asociativo siempre que
x*y*z = x*(y*z) para toda x, y pertenecientes a S.
3. Ley conmutativa.
Un operador binario (*) para un conjunto S es conmutativo siempre que:
x*y = y*x para toda x,y pertenecientes a S.
4. Elemento identidad.
El conjunto S tendrá un elemento identidad multiplicativo “identidad (*)” en S si existe un e perteneciente a S con la propiedad e*x = x*e =e para cada x pertenecientes a S.
5. Inversa.
El conjunto S tiene un elemento identidad (e) con respecto al operador (*) siempre que para cada x perteneciente a S exista un elemento y perteneciente a S tal que x*y=e.
6. Ley distributiva.
Si el operador (*) y el operador (.), son operadores binarios de S, (*) se dice que es distributivo sobre (.).
Siempre que:
x*(y . z) = (x*y) . (x*z)
- El operador binario (+) define la adición.
- Identidad aditiva es el cero.
- La inversa aditiva define la sustracción.
- El operador binario (.) define la multiplicación.
- Identidad multiplicativa es 1.
- Inversa multiplicativa de A es igual a 1/A define la división esto es A * 1/A = 1
- La única ley distributiva aplicable es la de operador (.) sobre el operador +
(.) sobre (+) a (b +c)=(a.b) +(a.c)
Para definir formalmente el álgebra de Boole se emplean postulados de Huntington.
1.
a) Cierre con respecto al operador (+)
b) Cierre con respecto al operador (.)
2.
a) Un elemento identidad con respecto al operador (+), designado por el cero x+0 =0+x=x
b) Un elemento identidad con respecto al operador (.) designado por el uno x*1=1*x=x
3.
a) Conmutativo con respecto al operador (+) : x+y = y+x
b) Conmutativo con respecto al operador (.) : x*y =y*x
4.
a) El operador (.) es distributivo sobre el operador (+) : x.(y+z) = (x.y) + (y.z)
b) El operador (+) es distributivo sobre el operador (.) : x+(x.z) = (x+y) . (x+z)
5. Para cada elemento de x pertenencia a B existe un elemento x' complemento perteneciente a B denominado complemento de x tal que:
a) x+x' = 1
b) x' = 0
6. Existen cuando menos dos elementos x,y pertenecientes a B tal que x diferente de y. Por lo tanto tenemos que el álgebra de Boole difiere de la aritmética y del álgebra ordinaria en la sig:
a) Los postulados Huntington: no incluyen al ley asociativa, no obstante esta ley es valida para el álgebra booleana (para ambos operadores)
b) La ley distributiva del operador (+) sobre el operador (.) esto es: x+(y.z) = (x+y).(x+z), la cual es valida para el álgebra de boole pero no para el álgebra ordinaria.
c) El álgebra booleana no tiene inversa aditiva a multiplicativa, por lo tanto no hay operaciones de sustracciones o división.
d) El postulado 5 define un operador llamado completo que no se encuentra en el álgebra ordinaria.
e) En el álgebra de Boole se define un conjunto B de dos elementos (0 y 1) y el álgebra ordinaria trata con el conjunto de los números reales.
Postulado 2 a) x + 0 = x b) x . 1 = x
Postulado 5 a) x + x' = 1 b) x . x' = 0
Teorema 1 a) x + x = x b) x . x = x
Teorema 2 a) x + 1 = 1 b) x . 0 = 0
Teorema 3 involución (x')' = x
Teorema 3 conmutativo a) x + y = y + x b) xy = yx
Teorema 4 asociativo a) x + (y + z) = (x + y) +z b) x (yz) = (xy) z
Postulado 4 distributivo a) x (y + z) = xy +xz b) x + yz = (x + y)(x +z)
Teorema 5 morgan a) ( x + y)' = x' y' b) (xy) = x' + y'
Teorema 6 absorción a) x + xy = x b) x (x + y) = x
Ejemplos:
x + x = x x + xy = x
x + x = (x + x) . 1 x . 1 + xy = x
x + x = (x + x) (x + x') x (1 + y) = x
x + x = x + xx' x (y + 1) = x
x + x = x + 0 x (1) = x
x + x = x x = x
Las variables booleanas pueden tomar varios valores de 1 ó 0.
Una función booleana es una expresión formada por variables binarias.
Ejemplo:
F1 = xyz'
Para F1 considerar que es igual a 1 si:
x = 1; y = 1 ; z' = 1; de otra manera F1 = 0.
Por lo tanto tendremos que una función booleana también puede representarse en una tabla de verdad. Para representar una función booleana en una tabla de verdad se necesita una lsit de 2ncombinaciones de 1 y 0 de las n variables binarias, y una columna que muestra combinaciones para las cuales f es igual a 1 ó 0.
x y z F1 F2 F3 F4
0 0 0 0 0 1 0
0 0 1 0 1 0 0
0 1 0 1 0 0 0
0 1 1 1 1 1 1
1 0 0 1 0 0 1
1 0 1 0 0 1 1
1 1 0 1 1 1 1
1 1 1 0 1 0 1
F1 = x'yz' + x'yz + xy'z + xyz' = x'y (z+z') + xz' (y+y') = x'y + xz'
F2 = x'y'z + x'yz + xyz' + xyz = x'z (y+y') + xy (z+z') = x'z + xy
F3 = x'y'z' + x'yz + xy'z + xyz'
F4 = x'y'z + xy'z' + xy'z + xyz' + xyz
= xy' (z+z') + xy (z+z') + x'yz
= xy' + xy + x'yz
= x (y+y') + x'yz
= x + x'yz
2.2. Funciones Lógicas
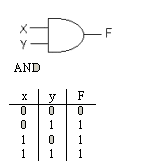
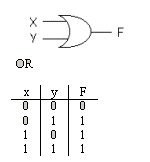
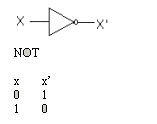
Manipulación algebraica
Cuando una función se incrementa con compuertas lógicas, cada literal en la función denota una entrada a una compuerta.
1. Cada literal denota la entrada a una compuerta.
2. Cada termino se implanta con una compuerta.
Por el momento nos limitaremos a la minimización por literales. Por lo cual debe quedar muy claro que en la manipulación algebraica no hay reglas especificas a seguir a que garanticen la respuesta final.
Ejemplo: Reducir las siguientes funciones booleanas.
1. x (x'+y) = xx' + xy = xy
2. x'y'z + x'yz + xy = x'z (y+y') + xy = x'z + xy
3. x + x'y = (x+x')(x+y) = x+y
Complemento de una función.
El complemento de una función F es F' obteniéndose por el intercambio de 1's y 0's y de 0's y 1's.
Ejemplo:
(A+B+C)' = (A+X)' para X = B+C
A' . X' ? A' . (B+C)' ? A' . B' .C'
(A+B+C+D+E+F+……..I)
(A'.B'.C'.D'.E'.F'…….I')
La forma generalizada de D'Morgan enuncia que el complemento de una función se obtiene del intercambio de los operadores AND y OR y complementando cada literal.
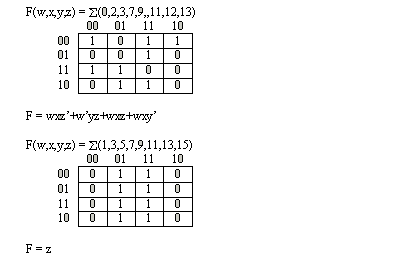
F1 = (x'yz' + x'y'z)' = (x+y'+z . x+y+z')
F2 = ? x (y'z'+yz)? = x' + ? x (y+z).(y'+z')?
Otra forma más simple para derivar el complemento de una función es tomar el dual de la función y complementar cada literal.
Hay que recordar que el cual de una función se obtiene por el intercambio de los operadores AND y OR y los 1's y los 0's.
Ejemplo:
F1 = x'yz' + x'y'z
el dual: F1 = (x+y'+z) . (x+y+z')
Las variables pueden ser normales (x) ó complemento (x').
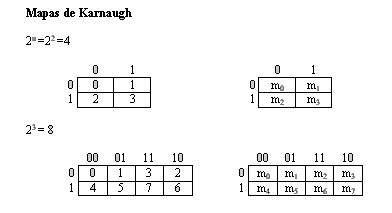
Cuando tenemos un conjunto de n variables nosotros podemos formar 2n miniterminos de acuerdo a la siguiente tabla:
Para n=3 2n-1 combinaciones iniciando a partir de cero.

Cada minitérmino lo obtenemos de un término AND de las n variables y complementado cada variable si el número binario que representa es un 0 y no complementando si es un 1.
Cada minitermino se representa por mj donde j representa el equivalente decimal del número binario del minitermino de la misma forma podemos tener los maxiterminos con las n variables formando un término OR para cada maxitermino.
En estas se hace la consideración de que cada variable no complementada corresponde al bit 0 y complementada al bit 1.

F1= x'y'z + xy'z' + xyz = m1+m4+m7
F2= x'yz + xy'z + xyz' + xyz = m3+m5+m6+m7
F1'= x'y'z' + x'yz' + x'yz + xy'z + xyz'
(F1')' = (x+y+z) . (x+y'+z) . (x+y'+z') . (x'+y+z') . (x'+y'+z)
= M0 . M2 . M3 . M5 . M6
El complemento de una función booleana lo podemos obtener al formar miniterminos para cada combinación que produce un cero en la función y aplicando el operador OR a esos términos.
Las funciones booleanas expresadas como una suma de miniterminos o productos de maxiterminos se dice que esta en forma canónica.
2.3. Simplificacion de Funciones
Suma de miniterminos.
Como sabemos cualquier función booleana puede expresarse como una suma de miniterminos. La suma de estos elementos que son los que definen una función booleana son aquellos que dan los 1's de la función en una tabla de verdad.
Algunas veces es conveniente expresar la función booleana en la forma de suma de miniterminos. Si no puede hacerse en esta forma entonces puede realizarse primero por la expansión de la expresión en una suma de los términos AND.
Después cada término se inspecciona para ver si contiene todas las variables, si se han perdido una o más variables, se aplica el operador AND con una expresión x+x' en donde x es una de las variables perdidas.
Ejemplo: Expresar la función F = A+B'C en una suma de miniterminos.
F= A+B'C
F(A,B,C)
A= A(B+B') = AB+AB'
= AB(C+C') + AB'(C+C')
= ABC + ABC' + AB'C +AB'C'
B'C = B'C (A+A')
= AB'C + A'B'C
F = ABC+ABC'+AB'C+AB'C'+AB'C+A'B'C
F = A'B'C+AB'C' +AB'C+ABC'+ABC
F = m1+ m4+m5+ m6+ m7
F(A,B,C)=SUM(1,4,5,6,7)
La sumatoria representa al operador OR que opera en los términos y números siguientes son los minitérminos de la función.
Las letras entre paréntesis que siguen a F forman una lista de las variables en el orden tomado cuando el minitérmino se convierte en un término AND.
Producto de los maxitérminos.
Para expresar una función booleana como un producto de maxitérminos, primero debe llevarse a una forma de términos OR. Esto es posible al uso de la ley distributiva; esto es si x+yz = (x+y) (x+z); para cualquier variable perdida x en cada término se opera a OR con xx'.
Ejemplo:
F = (x'+y) (x+z) (y+z)
(x'+y) = x'+y+zz'
= (x'+y+z) (x'+y+z)
(x+z) = x+z+yy'
= (x+y+z) (x+y'+z)
(y+z) = y+z+xx'
= (x+y+z) (x'+y+z)
F = (x'+y+z) (x'+y+z') (x+y+z) (x+y'+z) (x+y+z) (x'+y+z)
F = (x'+y+z) (x'+y+z') (x+y+z) (x+y'+z)
F = (x+y+z) (x+y'+z) (x'+y+z) (x'+y+z')
M0 M2 M4 M5
F(x,y,z) = PI(0,2,4,5)
El operador PI denota la operación AND de maxitérminos; y los números son los maxitérminos de la función.
Conversión entre formas canónicas.
El complemento de una función expresada como suma de minitérminos es igual a la suma de los minitérminos perdidos de la función original.
Ejemplo:
F(A,B,C) = SUM(1,4,5,6,7)
F'(A,B,C) = SUM(0,2,3) = m0+m2+m3
Si obtenemos el complemento de F' porque el teorema de D'Morgan se obtiene F en una forma diferente.
(F')' = (m0+m2+m3)' = m0'.m2'.m3' = M0 . M2 . M3 = PI(0,2,3)
= (x+y+z) . (x+y'+z) . (x+y'+z')
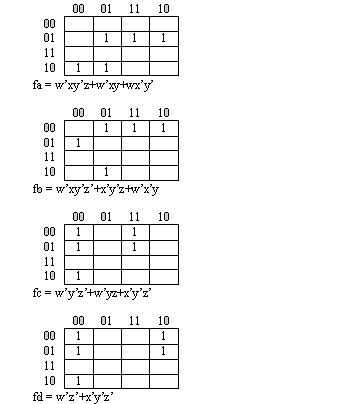
F = A'D+BD+B'D
A'D = A'D(B+B')
= A'BD+A'B'D
= A'BD(C+C') = A'BCD+A'BC'D
= A'B'D(C+C') = A'B'CD+A'B'C'D
BD = BD(A+A')
= ABD+A'BD
= ABD(C+C') = ABCD+ABC'D
= A'BD(C+C') = A'BCD+A'BC'D
B'D = B'D(A+A')
= AB'D+A'B'D
= AB'D(C+C') = AB'CD+AB'C'D
= A'B'D(C+C') = A'B'CD+A'B'C'D
F = A'BCD+A'BC'D+A'B'CD+A'B'C'D+ABCD+ABC'D+AB'CD+AB'C'D
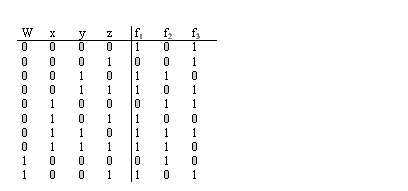


3.1. COMPARADORES DE MAGNITUD
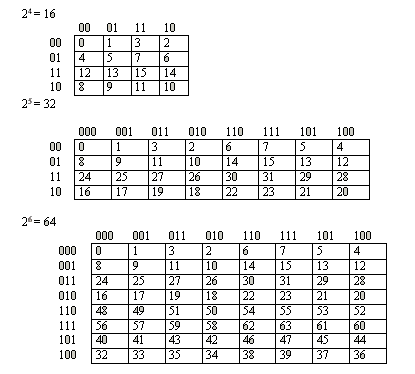
Un comparador de magnitud es un circuito combinacional que compara dos números A,B y determina sus magnitudes relativas. El resultado de la comparación se especifica por medio de tres variables binarias que indican:
A>B, A=B, A<B.
Un circuito para comparar dos números de n bits tiene 22n entradas en la tabla de verdad y se vuelve muy complicado aun para n=3 (64 combinaciones).
Considérense los números A,B cada uno con cuatro dígitos y escríbanse los coeficientes de los números en orden significativo descendente de la siguiente manera:
A= A3 A2 A1 A0 y B= B3 B2 B1 B0
Los dos números son iguales si todos los pares significativos son iguales, es decir A3=B3, A2=B2, A1=B1,A0=B0
Cuando los números son binarios los dígitos son 1 o 0 y la relación de igualdad para cada par de bits puede expresarse lógicamente con una función de equivalencia
Xi = Ai Bi + Ai` Bi`
I= 0,1,2,3,.......
Donde Xi es igual a 1 solamente si el par de bits en la posición i son iguales, es decir, si ambos son unos o ceros.
(A=B) = X3 X2 X1 X0
La variable binaria ( A=B ) es igual a 1 si todos los pares de dígitos de los dos números son iguales.
Para determinar si A>B se inspeccionan las magnitudes relativas de los pares de dígitos significativos comenzando desde la posición significativa mas alta. Si los dígitos son iguales, se compara el siguiente par de dígitos menos significativos, esta comparación continua hasta que se encuentre un par de dígitos diferente.
Si el correspondiente dígito de A es 1 y el dígito de B es 0, se concluye que A>B. Si el correspondiente dígito de A es 0 y el de B es 1 se tiene que A<B. La comparación secuencial puede expresarse lógicamente por las dos funciones de Bool que ha continuación se lista:
(A>B) = A3B3` + X3A2B2` + X3X2A1B1` + X3X2X1A0B0`
(A<B) = A3`B3 + X3A2'B2 + X3X2A1`B1 + X3X2X1A0'B0
Los símbolos (A>B) y ( A<B) son variables de salida binaria que son iguales a 1 cuando (A>B) o (A<B) respectivamente.
COMPARADOR DE MAGNITUD DE 3 BITS

SUMADORES Y RESTADORES

DIAGRAMA DE UN MEDIO SUMADOR

SUMADOR COMPLETO

DIAG. DE SUMADOR COMPLETO CON COMPUERTAS AND Y OR

DIAG. SUMADOR COMPLETO CON COMPUERTAS XOR, AND Y OR

DIAG.SUMADOR COMPLETO CON COMPUERTAS XOR Y NAND

SUMADOR BINARIO EN PARALELO

DIAGRAMA DE SUMADOR BINARIO EN PARALELO

MEDIO RESTADOR

F(b) = X'Y + XY'
F(d) = X'Y
DIAGRAMA DE MEDIO RESTADOR

RESTADOR COMPLETO

DIAG. RESTADOR COMPLETO CON COMPUERTAS AND Y OR

4.1. Introducción
Los circuitos lógicos para sistemas digitales pueden ser combinacionales o secuenciales. Un circuito combinacional consta de compuertas lógicas cuyas salidas en cualquier momento están determinadas en forma directa por la combinación presente de las entradas sin tomar en cuenta las entradas previas.
Un Circuito combinacional realiza una operación específica de procesamiento de información, especificada por completo en forma lógica por un conjunto de funciones booleanas. Los circuitos secuenciales emplean elementos de memoria (celdas binarias) además de las compuertas lógicas. Sus salidas son una función de las entradas y el estado de los elementos de memoria.
El estado de los elementos de memoria, a su vez, es una función de las entradas previas. Como consecuencia, las salidas de un circuito secuencial dependen no sólo de las entradas presentes, sino también de las entradas del pasado y, el comportamiento del circuito debe especificarse en una secuencia de tiempo de entradas y de estados internos. En la unidad 5 se exponen los circuitos secuenciales.
En la unidad 1 se aprendió a reconocer los números binarios y los códigos binarios que representan cantidades discretas de información. Estas variables binarias se representan por voltajes eléctricos o alguna otra señal. Las señales pueden manipularse en las compuertas lógicas digitales para realizar las funciones requeridas.
En la unidad 2 se introdujo el álgebra booleana como una forma para expresar de manera algebraica las funciones lógicas. También se aprendió cómo simplificar las funciones booleanas para lograr la implementación económica de compuertas.
El objetivo de esta unidad es usar el conocimiento adquirido en los capítulos previos y formular varios procedimientos sistemáticos de diseño y análisis de los circuitos combinacionales. La solución de algunos ejemplos típicos proporcionará un catálogo útil de funciones elementales importantes para el entendimiento de las computadoras y sistemas digitales.
Un circuito combinacional consta de variables de entrada, compuertas lógicas y variables de salida. Las compuertas lógicas aceptan las señales de las entradas y generan señales a las salidas. Este proceso transforma la información binaria de los datos dados de entrada en los datos requeridos de salida. En forma obvia, tanto los datos de entrada y salida se representan por señales binarias, esto es, existen en dos valores posibles, uno representa la lógica 1 y el otro la lógica O.
Para las n variables de entrada, hay 2 a la n combinaciones posibles de los valores binarios de entrada. Para cada combinación posible de entrada, hay una y sólo una combinación posible de salida. Un circuito combinacional puede describirse por n funciones booleanas, una para cada variable de salida. Cada función de salida se expresa en términos de las n variables de entrada.
Cada variable de entrada a un circuito combinacional puede tener uno o dos alambres. Cuando está disponible sólo un alambre, puede representar la. variable, ya sea en la forma normal (sin prima) o en la forma complementaria (con prima).
Ya que una variable en una expresión booleana puede aparecer con prima y/o sin prima, es necesario proporcionar un inversor para .cada .literal que no está disponible en el alambre de entrada, por otra parte, una variable. de entrada puede. aparecer. en dos alambres, suministrando las formas tanto normal como complementaria, a la entrada del circuito.
En este caso no es necesario incluir inversores para las entradas, El tipo de celdas binarias utilizadas en. la mayoría de los sistemas digitales son circuitos flip-flop, que tienen salidas para los valores tanto normal como complementario de la variable binaria almacenada.
4.2. Procedimiento
El diseño de los circuitos combinacionales surge del planteamiento verbal del problema y termina en un diagrama de circuito lógico, o un conjunto de funciones booleanas del cual puede obtenerse con facilidad el diagrama lógico. El procedimiento sigue estos pasos:
1. Se enuncia el problema.
2. Se determina el número de las variables de entrada disponibles y de las variables de salida requeridas.
3. Se asignan símbolos de letra a las variables de entrada y salida.
4. Se deriva la tabla de verdad que define las relaciones requeridas entre las entradas y las salidas.
5. Se obtiene la función booleana simplificada para cada salida.
6. Se dibuja el diagrama lógico.
Una tabla de verdad para un circuito combinacional consta de columnas de entrada y columnas de salida. Los 1 y O en las columnas de entrada se obtienen de las 2n combinaciones binarias disponibles para las n variables de entrada. Los valores binarios para las salidas se determinan del examen del problema enunciado. Una salida puede ser igual ya sea a O ó 1 para cada combinación válida de entrada. Sin embargo, las especificaciones pueden indicar que algunas combinaciones de entrada no ocurrirán. Estas combinaciones se vuelven condiciones no importa.
Las funciones de salida que se especifican en la tabla de verdad dan la definición exacta del circuito combinacional. Es importante que las especificaciones verbales se interpreten correctamente en una tabla de verdad. Algunas veces el diseñador debe usar su intuición y experiencia para llegar a la interpretación correcta. Las especificaciones verbales rara vez son muy completas y exactas. Cualquier interpretación equivocada que resulte en una tabla de verdad incorrecta producirá un circuito combinacional que no cubriría los requisitos enunciados.
Las funciones booleanas de salida de la tabla de verdad se simplifican por cualquier método disponible, como manipulación algebraica, el método de mapa, o el procedimiento de tabulación. Por lo común, habrá una variedad de expresiones simplificadas a elegir.
No obstante, en cualquier aplicación particular ciertas restricciones, limitaciones y criterios servirán como guía en el proceso de escoger una expresión algebraica particular. Un método práctico de diseño sería tener que considerar tales restricciones como (1) número mínimo de compuertas, (2) número mínimo de entradas a una compuerta, (3) tiempo mínimo de propagación de la señal a través del circuito, (4) número mínimo de interconexiones y (5) limitaciones de las capacidades de impulsión de cada compuerta.
Ya que todos estos criterios no pueden satisfacerse en forma simultánea, y ya que la importancia de cada restricción se dicta por la aplicación particular, es difícil hacer un enunciado general de lo que constituye una simplificación aceptable. En la mayoría de los casos, la simplificación principia por satisfacer un objetivo elemental, como producir una función booleana, simplificada en una forma estándar y proceder de ese punto a cumplir cualesquiera otros criterios de comportamiento.
En la práctica, los diseñadores tienden, a ir de la función booleana a una lista de alambrado que muestra las interconexiones entre varias compuertas lógicas estándar. En este caso, el diseño no va más allá de la función booleana simplificada de salida requerida. Sin embargo, un diagrama lógico es de ayuda para visualizar la implementación de compuertas de las expresiones.
4.3. Sumadores
Las computadoras digitales realizan una variedad de tareas de procesamiento' de información. Entre las funciones básicas encontradas están las diversas operaciones aritméticas. Sin duda, la operación aritmética más básica es la adición de dos dígitos binarios. Esta adición simple consta de cuatro operaciones elementales posibles, a saber, O + O = O, O + 1 = 1, 1 + O = 1 y 1+ 1 = 10.
Las primeras tres operaciones producen una suma cuya longitud es un dígito, pero cuando tanto los bits sumando como adendo son iguales a 1, la suma binaria consta dedos dígitos. El bit significativo más alto de este resultado se denomina acarreo. Cuando los números sumando y adendo contienen más dígitos significativos, la cuenta que se lleva obtenida por la adición de dos bits se añade al siguiente par de orden más alto de bits significativos.
Un circuito combinacional que lleva a cabo la adición de dos bits se denomina medio sumador. Uno que lleva a cabo la adición de tres bits (dos bits significativos y una cuenta que se lleva previa) es un sumador completo. El nombre del primero proviene del hecho de que dos medios sumadores se emplean para implementar un adicionador completo.
Medio Sumador
De la explicación verbal del medio sumador, se encuentra que este circuito necesita dos entradas binarias y dos salidas binarias. Las variables de entrada designan los bits sumando y adendo; las variables de salida producen la suma y el acarreo. Es necesario especificar dos variables de salida debido a que el resultado puede constar de dos dígitos binarios. Se asignan en forma arbitraria los símbolos x y y a las dos entradas y S (de suma) y C (para el acarreo) a las salidas.
Ahora que se han establecido el número y nombres de las variables de entrada y salida, ya puede formularse una tabla de verdad para identificar en forma exacta la función del medio sumador. Esta tabla de verdad se muestra a continuación:
x y C S
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0
El acarreo de salida es 0 a menos que ambas entradas sean 1. La salida S representa el bit menos significativo de la suma.
La función booleana simplificada de las dos salidas puede obtenerse de manera directa mediante la tabla de verdad. Las expresiones simplificadas en suma de productos son:
S = x'y + xy'
C = xy
Sumador Completo
Un sumador completo es un circuito combinacional que formar la suma aritmética de tres bits de entrada. Consta de tres entradas y dos salidas. Dos de las variables de entrada, que se indican por x y y se presentan los dos bits significativos que van a añadirse. La tercera entrada, z, representa la cuenta que se lleva de la posición previa significativa más baja.
Son necesarias dos salidas debido a que la suma aritmética de tres dígitos binarios varia en valor desde 0 a 3 y el 2 o 3 binarios requieren dos dígitos. Las dos salidas se denotan por los símbolos S para suma y C para la cuenta que se lleva. La variable. binaria S da el valor del bit menos significativo de la suma. La variable binaria C da la cuenta que se lleva de salida. La tabla de verdad del sumador completo es como sigue:
x y z | C S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
Los ocho renglones bajo las variables de entrada denotan todas las combinaciones posibles de 1 y 0 que pueden tener esas variables. Los 1 y 0 de las variables de salida se determinan de la suma aritmética de los bits de entrada. Cuando todos los bits de entrada son 0, la salida es 0. La salida S es igual a 1 sólo cuando una entrada es igual a 1, o cuando todas las tres entradas son iguales a 1. La salida C tiene una cuenta que se lleva de 1 si dos o tres entradas son iguales a 1.
Los bits de entrada y salida del circuito combinacional tienen diferentes interpretaciones en las diversas etapas del problema. En forma física las señales binarias de los alambres de entrada se consideran dígitos binarios agregados de manera aritmética para dar una suma de dos dígitos a los alambres de salida. Por otra parte, los mismos valores binarios se consideran variables de funciones booleanas cuando se expresan en la tabla de verdad o cuando el circuito se implementa con compuertas lógicas. Es importante darse cuenta de que se dan dos interpretaciones diferentes a los valores de los bits que se encuentran en este circuito.
La relación lógica de entrada-salida del circuito sumador completo puede expresarse en dos funciones booleanas, una para cada variable de salida. Cada función booleana de salida requiere un mapa único para su simplificación. Cada mapa debe tener ocho cuadros, ya que cada salida es una función de tres variables de entrada.
4.4. Restadores
La sustracción de dos números binarios puede llevarse a cabo tomando el complemento del sustraendo y agregándolo al minuendo. Por este método, la operación de sustracción, llega a ser una operación de división que requiere sumadores completos para su implementación en máquina. Es posible implementar la sustracción con circuitos lógicos en una forma directa, como se hace con lápiz y papel.
Por este método cada bit sustraendo del número se sustrae de su bit minuendo correspondiente significativo para formar un bit de diferencia. Si el bit minuendo es menor que el bit sustraendo, se toma un 1 de la siguiente posición significativa. El hecho de que se ha tomado un 1 debe llevarse al siguiente par más alto de bit mediante una señal binaria que llega de fuera (salida) de una etapa dada y va a (entrada) la siguiente etapa más alta. En forma precisa así como hay medio sumadores y sumadores completos, hay medio restadores y restadores completos.
Medio restador
Un medio restador es un circuito combinacional que sustrae dos bits y produce su diferencia. También tiene una salida para especificar si se ha tomado un 1. Se designa el bit minuendo por x y el bit sustraendo mediante y. Para llevar a cabo x - y, tienen que verificarse las magnitudes relativas de x y y. Si x > y se tienen tres posibilidades; 0 - 0 = 0, 1 - 0 = 1 y, 1 - 1 = 0. El resultado se denomina bit de diferencia.
Si x < y. tenemos 0 - 1 y es necesario tomar un 1 de la siguiente etapa más alta.
El 1 que se toma de la siguiente etapa más alta añade 2 al bit minuendo, de la misma forma que en el sistema decimal lo que se toma añade 10 a un dígito minuendo. Con el minuendo igual a 2, la diferencia llega a ser 2 - 1 = 1. El medio restador requiere dos salidas. Una salida genera la diferencia y se denotará por el símbolo D. La segunda salida, denotada B para lo que se toma, genera la señal binaria que informa a la siguiente etapa que se ha tomado un 1. La tabla de verdad para las relaciones de entrada-salida de un medio restador ahora puede derivarse como sigue:
x y | B D
0 0 0 0
0 1 1 1
1 0 0 1
1 1 0 0
La salida que toma B es un 0 en tanto que x > y. Es un l para x = 0 y y = 1. La salida D es el resultado de la operación aritmética 2B + x - y.
Las funciones booleanas para las dos ,salidas del medio restador se derivan de manera directa de la tabla de verdad,
D = x' y + x y'
B = x' y
Es interesante observar que la lógica para D es exactamente la misma que la lógica para la salida S en el medio sumador.
Restador completo
Un restador completo es un circuito combinacional que lleva a cabo una sustracción entre dos bits, tomando en cuenta que un 1 se ha tomado por una etapa significativa más baja. Este circuito tiene tres entradas y dos salidas. Las tres entradas, x, y y z, denotan al minuendo, sustraendo y a la toma previa, respectivamente. Las dos salidas, D y B, representan la diferencia y la salida tomada, respectivamente. La tabla de verdad para el circuito es como sigue:
x y z | B D
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 1 0
1 0 0 0 1
1 0 1 0 0
1 1 0 0 0
1 1 1 1 1
Los ocho renglones bajo las variables de entrada designan todas las combinaciones posibles de 1 y 0 que pueden tomar las variables binarias. Los 1 y 0 para las variables de salida están determinados por la sustracción de x - y - z.
Las combinaciones que tienen salida de toma z = 0 se reducen a las mismas cuatro condiciones del medio sumador. Para x = 0,, y = 0 y z = 1, tiene que tomarse un 1 de la siguiente etapa, lo cual hace B = 1 y añade 2 a x. Ya que 2 - 0 - 1 = 1, D = 1. Para x = 0 y yz = 11, necesita tomarse otra vez, haciendo B = 1 y x = 2.
Ya que 2 - 1 - 1 = 0, D = 0. Para x = 1 y yz = 01, se tiene x - y - z = 0, lo cual hace B = 0 y D = 0. Por último, para x = 1, y = l, z = 1, tiene que tomarse 1, haciendo B = 1 y x = 3 y, 3 - 1 - 1 = 1, haciendo D = 1.
4.5. Convención de Código
La disponibilidad de una gran variedad de códigos para los mismos elementos discretos de información origina el uso de códigos diferentes por sistemas digitales diferentes. Algunas veces es necesario usar la salida de un sistema como la entrada a otro. Debe insertarse un circuito de conversión entre los dos sistemas si cada uno utiliza códigos diferentes para la misma información. Así que, un convertidor de código es un circuito que hace dos sistemas compatibles aun cuando cada uno use un código binario diferente.
4.6. Procedimiento de Análisis
El diseño de un circuito combinacional se inicia con las especificaciones verbales de una función requerida y culmina con un conjunto de funciones booleanas de salida o un diagrama lógico. El análisis de un circuito combinacional es en cierta forma el proceso inverso. Principia con un diagrama lógico dado y termina con un conjunto de funciones booleanas, una tabla de verdad o una explicación verbal de la operación del circuito.
Si el diagrama lógico que va a analizarse se acompaña con una función nombre o una explicación de lo que se supone que realiza, entonces el problema del análisis se reduce a una verificación de la función enunciada.
El primer paso en el análisis es tener la seguridad de que el circuito dado es combinacional y no secuencial. El diagrama de un circuito combinacional tiene compuertas lógicas sin trayectorias de retroalimentación o elementos de memoria. Una trayectoria de retroalimentación es una conexión de la salida de una compuerta a la entrada de una, segunda compuerta que forma parte de la entrada a la primera compuerta. Las trayectorias de retroalimentación o elementos de memoria en un circuito digital definen un circuito secuencial.
Una vez que se ha verificado que el diagrama lógico es un circuito combinacional, puede procederse a obtener las funciones booleanas de salida y/o la tabla de verdad. Si el circuito está acompañado por una explicación verbal de su función, entonces las funciones booleanas o la tabla de verdad son suficientes para la verificación. Si la función del circuito está bajo investigación, entonces es necesario interpretar la operación del circuito mediante la tabla de verdad derivada. El éxito de tal investigación se favorece si se tiene experiencia previa y familiaridad con una amplia variedad de circuitos digitales. La habilidad para correlacionar una tabla de verdad con una tarea de procesamiento de información es un arte que se adquiere con la experiencia.
Para obtener las funciones booleanas de salida de un diagrama lógico, se procede como sigue:
1. Se etiquetan con símbolos arbitrarios todas las salidas de compuerta que son una función de las variables de entrada. Se obtienen las funciones booleanas para cada compuerta.
2. Se etiqueta con otros símbolos arbitrarios las compuertas que son una función de las variables de entrada y/o compuertas previamente etiquetadas. Se encuentran las funciones booleanas para esas compuertas..
3. Se repite el proceso delineado en el paso 2 hasta que se han obtenido las salidas del circuito.
4. Por sustitución repetida de las funciones previamente definidas, se obtienen las funciones booleanas de salida en términos sólo de las variables de entrada.
4.7. Circuitos Nand de Nivel Múltiple
Los circuitos combinacionales se construyen más a menudo con compuertas NAND o NOR más bien que con compuertas ÁND y OR. Las compuertas NAND y NOR son más comunes desde el punto de vista del hardware, ya que están disponibles en la forma de circuitos integrados.
Debido a la preeminencia de las compuertas NAND y NOR en el diseño de los circuitos combinacionales, es importante tener la capacidad de reconocer las relaciones que existen entre los circuitos construidos con compuertas AND OR y sus diagramas equivalentes NAND o NOR.
4.8. Circuitos Nor de Niveles Múltiples
La función NOR es la dual de la función NAND. Por esta razón, todos los procedimientos para la lógica NOR forman un dual de los procedimientos y reglas correspondientes desarrollados para la lógica NAND. En esta sección se enumeran diversos métodos para la implementación y análisis de la lógica NOR por el seguimiento de la misma lista de tópicos usados para la lógica NAND.
5.1 INTRODUCCION.
Los circuitos digitales que hasta ahora se han considerado, han sido combinacionales, esto es, las salidas en cualquier momento dependen por completo de las entradas presentes en ese tiempo. Aunque cualquier sistema digital es susceptible de tener circuitos combinacionales, la mayoría de los sistemas que se encuentran en la practica también incluyen elementos de memoria, los cuales requieren que el sistema se describa en términos de Lógica Secuencial.
Un diagrama a bloques de un circuito secuencial consta de un circuito combinacional al que se conectan elementos de memoria para formar una trayectoria de retroalimentación. Los elementos de memoria son dispositivos capaces de almacenar dentro de ellos información binaria. La información binaria almacenada en los elementos de memoria en cualquier dado se define como el estado del circuito secuencial.
El circuito secuencial recibe información binaria de entradas externas. Estas entradas, junto con el estado
presente de los elementos de memoria, determinan el valor binario en las terminales de salida. También determinan las condiciones para cambiar el estado en los elementos de memoria.
Hay dos tipos principales de circuitos secuenciales. Su clasificación depende del temporizado de sus señales. Un circuito secuencial sincrono es un sistema cuyo comportamiento puede definirse por el conocimiento de sus señales en instantes discretos de tiempo. El comportamiento de un circuito secuencial asíncrono depende del orden en el cual cambian sus señales de entrada y puede afectarse en cualquier instante de tiempo. Los elementos de memoria que por lo común se utilizan en los circuitos secuenciales asíncronos son dispositivos de retardo de tiempo. La capacidad de memoria de un dispositivo de retardo de tiempo se debe al hecho de que toma un tiempo finito para que la señal se propague a través del dispositivo.
Un sistema lógico secuencial asíncrono, por definición, debe emplear señales que afecten los elementos de memoria solo en instantes discretos de tiempo. Una forma de lograr este objetivo es usar pulsos de duración limitada a través del sistema, de modo que una amplitud de pulso represente la lógica 1 y otra amplitud (o la ausencia de pulso) represente la lógica 0.
Los sistemas lógicos secuenciales sincronos utilizan amplitudes fijas, como niveles de voltaje para señales binarias. La sincronización se logra a través de un dispositivo sincronizador llamado reloj maestro generador, el cual genera un tren periódico de pulsos de reloj. Los pulsos de reloj se distribuyen a través del sistema de tal forma que los elementos de memoria están afectados solo por la llegada del pulso de sincronización.
Los elementos de memoria que se utilizan en los circuitos secuenciales de reloj se llaman flip-flops estos circuitos son celdas binarias capaces de almacenar un bit de informaron. Un circuito flip-flop tiene dos salidas, una para el valor normal y otra para el valor complementario del bit almacenado en el. la información binaria puede entrar a un flip-flop es una gran variedad de formas, hecho que da lugar a diferentes tipos de flip-flops.
5.2. FLIP-FLOPS.
Un circuito flip-flop puede mantener un estado binario en forma indefinida (en cuanto se suministre potencia al circuito) hasta que recibe la dirección de una señal de entrada para cambiar de estado. La diferencia principal entre los diversos tipos de flip-flops esta en el numero de entradas que poseen y en la manera en la cual las entradas afectan el estado binario.
Circuito Básico Flip-Flop
Como ya se menciono anteriormente, estos circuitos pueden construirse con compuertas NAND o dos compuertas NOR. Cada circuito forma un flip-flop básico, La conexión y el acoplamiento cruzado mediante la salida de una compuerta a la entrada de otra constituye una trayectoria de retroalimentación. Por esta razón los circuitos se clasifican como secuenciales asíncronos. Cada flip-flop tiene dos salidas Q y Q', y dos entradas, SET para ajustar y RESET para restaurar. A este tipo de flip-flop se les llama RS directamente acoplado o seguro.
Un flip-flop tiene dos estados utilies, cuando Q=1 y Q'=0, esta en el estado ajuste (o estado 1). Cuando Q=0 y Q'=1, esta en el estado despejado (o estado 0). Las salidas Q y Q' son complementarias la una de la otra y se refieren como las salidas normal y complementaria, respectivamente. El estado binario del flip-flop se toma para que sea el valor de la salida normal.
Bajo operación normal, ambas entradas permanecen en 0 a menos que tenga que cambiarse el estado de flip-flop. La aplicación de un 1 momentáneo a la entrada de ajuste provoca que el flip-flop pase al estado ajuste. La entrada ajuste debe volver a 0 antes de que un 1 se aplique a la entrada restaurar. Un 1 momentáneo aplicado a la entrada de restaurar causa que el flip-flop vaya al estado despejado. cuándo ambas entradas son inicialmente 0, un 1 aplicado a la entrada de puesto mientras el flip-flop esta en el estado despejado deja las salidas sin cambio. cuando se aplica un 1 a ambas entradas de ajuste y restaurar, ambas salidas pasan a 0, este estado del flip-flop es indefinido y por lo tanto se evita. si ambas entradas ahora van a 0, el estado del flip-flop es indeterminado y depende de cual entrada permanezca en 1 mas tiempo de la transición a 0.
5.2.1. FLIP-FLOP D
El flip-flop D es una modificación del RS con reloj. Las compuertas NAND 1 y 2 forman un flip-flop básico y las compuertas 3 y 4 se modifican para formar un flip-flop RS son reloj. La entrada D va en forma directa a la entrada S y su complemento, a través de la compuerta 5, se aplica a la entrada R. En tanto que el pulso de reloj en la entrada este en 0, las compuertas 3 y 4 tienen un 1 en sus salidas, sin importar el valor de las otras entradas. Esto se apega al requisito de que las entradas del flip-flop básico NAND permanezcan inicialmente en el nivel 1. La salida D muestrea durante la ocurrencia de un pulso de reloj. Si es 1, la salida de la compuerta 3 pasa a 0, cambiando el flip-flop al estado de ajuste (a menos de que ya este puesto), si es 0, la salida de la compuerta 4 va a 0, cambiando el flip-flop al estado despejado.
El flip-flop tipo D recibe esta denominación debido a su capacidad de transferir "datos" en el flip-flop. En forma básica es un flip-flop RS con un inversor en la salida R, El inversor agregado reduce el numero de entradas de 2 a 1. La entrada CP con frecuencia recibe la designación variable G (gate) para indicar que esta entrada habilita el seguro con compuertas para hacer posible la entrada de información al circuito.
5.2.2. FLIP-FLOP JK
Un flip-flop JK es un refinamiento del RS ya que el estado indeterminado del RS se define en el JK. Las entradas J y K se comportan como las entradas S y R para ajustar y despejar el flip-flop. Cuando se aplican señales de entrada en forma simultanea a J como a k, el flip-flop cambia a su estado complementario, esto es si Q=1, cambia a Q=0 y viceversa.
En un flip-flop JK temporizado, la salida Q opera AND con las entradas K y CP, de modo que el flip-flop se despeja durante un pulso de reloj solo si Q era previamente 1. En forma similar, la salida Q' opera AND con las entradas J y CP de modo que el flip-flop se ajusta con un pulso de reloj solo si Q'era previamente 1.
Obsérvese que debido a la conexión de retroalimentación en el flip-flop JK, una señal CP permanece en 1 (en tanto J=K=1) una vez que las salidas se han complementado provocara transiciones repetidas y continuas de las salidas. Para evitar esta operación indeseable, los pulsos de reloj deben tener una duración mas corta que el retardo de propagación a través del flip-flop.
5.2.3. FLIP-FLOP T
El flip-flop tipo T es una versión de una sola entrada del flip-flop JK, el flip-flop T se obtiene mediante un tipo JK si ambas entradas se ligan. La denominación T proviene de la capacidad del flip-flop para conmutar (toggle), o cambiar de estado. Sin importar el estado presente del flip-flop, asume el estado complementario cuando ocurre el pulso de reloj mientras la entrada T es logica 1.
5.3. DISPARO DEL FLIP-FLOP
El estado de un flip-flop se cambia por una modificación momentánea en la señal de entrada. este cambio momentáneo se le denomina gatillo y la transición que provoca se dice que dispara el flip-flop. Los flip-flops asíncronos, como los circuitos básicos, requieren una entrada de gatillo definida por un cambio de nivel de señal. este nivel debe de volver a su valor inicial (0 en NOR y 1 en NAND) antes de que aplique un segundo gatillo. Los flip-flops temporizados se disparan por pulsos. Un pulso comienza desde un valor inicial de 0, pasa en forma momentánea a 1 y después de un corto tiempo, regresa a su valor 0 inicial. El intervalo de tiempo desde la aplicación del pulso hasta que ocurre la transición de la salida es un factor critico que requiere mas investigación.
Un pulso de reloj puede ser positivo o bien negativo. Una fuente positiva de reloj permanece 0 durante el intervalo entre pulsos y pasa a 1 al ocurrir un pulso. El pulso pasa a través de dos transiciones de señal: desde 0 a 1 y el regreso de 1 a 0, La transicion positiva se define como borde positivo y la transicion negativa como el borde negativo, esta definición también se aplica a los pulsos negativos.
Flip-Flop maestro-esclavo
Este arreglo, se construye mediante dos flip-flops separados. un circuito sirve como un maestro y el otro como un esclavo. Este circuito consta además de lo ya mencionado con un inversor. Cuando el pulso de reloj CP es 0, la salida del inversor es 1. Ya que la entrada de reloj del esclavo es , el flip-flop esta habilitado si la salida Q es igual a Y, en tanto que Q'es igual a Y'. El flip-flop maestro se habilita porque CP=0. Cuando el pulso llega a 1, entonces la información en las entradas externas R y S se transmiten al flip-flop maestro, sin embargo, el flip-flop esclavo esta aislado mientras el pulso este en su nivel 1, ya que la salida del inversor es 0. Cuando el pulso regresa a 0, el flip-flop maestro esta aislado, lo cual evita que lo afecten las entradas externas. el flip-flop esclavo pasa entonces al mismo estado que el flip-flop maestro.
El comportamiento del flip-flop maestro-esclavo que acaba de describirse dicta que los cambios de estado en todos los flip-flops coincidan con la transicion de borde negativo del pulso. No obstante, algunos flip-flops maestro-esclavo IC cambian los estados de salida en la transicion de borde positivos de los pulsos de reloj. Esto sucede en flip-flops que tienen un inversor adicional en la CP terminal y la entrada del maestro, tales se disparan con pulsos negativos de modo que el borde negativo del pulso afecte al maestro y el borde positivo afecte al esclavo y las terminales de salida.
Flip-Flop Disparo por Borde
Otro tipo de flip-flop que sincroniza los cambios de estado durante la transición de pulsos de reloj es el disparado por borde en este tipo de flip-flop, las transiciones de salida ocurren e un nivel especifico del pulso de reloj. Cuando el nivel del pulso de entrada excede el nivel umbral, las entradas están bloqueadas y, de este modo, el flip-flop no responde a los cambios adicionales en las entradas hasta que el pulso de reloj regresa a 0 y ocurre otro pulso. Algunos flip-flops disparados por borde provocan una transicion en el borde positivo del pulso y otros causan una transicion en el borde negativo del pulso.
5.4. ANALISIS DE CIRCUITOS SECUENCIALES TEMPORIZADOS.
El comportamiento de un circuito secuencial se determina mediante las entradas, las salidas y los estados de sus flip-flops. Tanto las salidas como el estado siguiente son función de las entradas y del estado presente. El análisis de los circuitos secuenciales consiste en obtener una tabla o un diagrama de las secuencias de tiempo de las entradas, salidas y los estados internos. También es posible escribir expresiones booleanas que describen el comportamiento de los circuitos secuenciales. Sin embargo, esas expresiones deben incluir la secuencia de tiempo necesaria ya sea en forma directa o indirecta.
Un diagrama lógico se reconoce como el circuito de un circuito secuencial e incluye flip-flops. los flip-flops pueden ser de cualquier tipo y el diagrama lógico puede o no incluir compuertas combinacionales.
5.5. DISEÑO DE CONTADORES.
Un circuito secuencial que pasa a través de una secuencia prescrita de estados bajo la aplicación de pulsos de entradas se denomina contador. Los pulsos de entrada, llamados pulsos de conteo pueden ser pulsos de reloj, o pueden originarse en una fuente externa y pueden ocurrir a intervalos de tiempo prescritos o aleatorios. En un contador, la secuencia de estados puede seguir un conteo binario o cualquier otra secuencia de estados.
Los contadores se encuentran en casi todo el equipo que contiene logica digital. Se usa para contar el numero de ocurrencias de un evento y son útiles para generar secuencias de temporizado para controlar operaciones con un sistema digital.
De las diversas secuencias que puede seguir un contador, la secuencia binaria directa es la mas simple y la mas directa. un contador que sigue la secuencia binaria se denomina contador binario un contador binario de n bits consta de n flip-flops y puede contar con un binario desde 0 hasta 2n-1.
La secuencia de conteo de un contador binario de 3 bits se da en una secuencia de conteo que se repite después que alcanza el ultimo valor, de modo que el estado 000 es el estado siguiente despues de 111. La secuencia de conteo da toda la informaron necesaria para diseñar el circuito. No es necesario listar los estados siguientes en una columna separada porque pueden leerse en el numero de la secuencia siguiente.
La tabla de excitación para un contador de 3 bits se designa por los tres flip-flops con variables A2,A0y A1. Los contadores binarios se construyen en la forma mas eficientes con los flip-flops T. La excitación flip-flop para las entradas T se derivan mediante la tabla de excitación del f-f tipo T y mediante la inspección de la transicion de estado desde un conteo dado (estado presente) al siguiente bajo el (estado siguiente).
Un contador con n flip-flops puede tener una secuencia binaria de menos de 2n números. Un contador BCD cuenta la secuencia binaria desde 0000 hasta 1001 y regresa a 0000 para repetir la secuencia. Otros contadores pueden seguir una secuencia arbitraria que es posible no sea la secuencia binaria directa. En cualquier caso, el procedimiento de diseño es el mismo. La secuencia de conteo se lista en la tabla de excitación que se obtiene al comparar un conteo presente con el siguiente conteo que se lista bajo el. Una secuencia de conteo tabulada siempre supone una cuenta repetida, de modo como el siguiente estado de la ultima entrada es el primer conteo listado.
5.6. REGISTROS.
Un circuito secuencial temporizado consta de un grupo de flip-flop y compuertas combinacionales
conectadas para formar una trayectoria de retroalimentación. Los flip-flop son esenciales porque, cuando están ausentes, el circuito se reduce a un circuito combinacional puro (siempre que no haya trayectoria de retroalimentación).
Un circuito solo con flip-flop se considera secuencial incluso cuando están ausentes las compuertas combinacionales. Un circuito MSI que contiene celdas de almacenamiento en su interior, es, por definición, un circuito secuencial. Los circuitos MSI que incluyen flip-flop por lo común mas por la función que realizan en vez de por el nombre "circuito secuencial". Estos circuitos MSI se clasifican en una de tres categorías: registros, contadores o memoria de acceso aleatorio.
Registros.
Un registro es un grupo de celdas de almacenamiento binario adecuadas para mantener información binaria. Un grupo de flip-flop constituye un registro, ya que cada flip-flop es una celda binaria capaz de almacenar un bit de información. Un registro de n-bit tiene un grupo de n flip-flop y es capaz de almacenar cualquier información binaria que contenga n bits. Además de los flip-flop, un registro puede tener compuertas combinacionales que realicen ciertas tareas de procesamiento de datos. en su definición mas amplia, un registro consta de un grupo de flip-flop y compuertas que efectúan una transicion. Los flip-flop mantienen la información binaria y las compuertas controlan cuando y como se transfiere información nueva al registro.
Están disponibles varios registros en la forma MSI. El registro mas sencillo consta de flip-flop solos sin ninguna compuerta externa. Un ejemplo es uno construido con cuatro flip-flop tipo D y una entrada común de pulsos de reloj. La entrada de pulso de reloj, CP, capacita todos los flip-flop de modo que la información presente disponible en las cuatro entradas puede transferirse al registro de 4-bit. Las cuatro salidas pueden muestrearse para obtener la información almacenada en ese momento en el registro.
La forma en que los flip-flop se disparan es importante. Si los flip-flop estan construidos con seguros de compuertas tipo D, entonces la información presentada en una entrada de información D se transfiere a la salida Q cuando el pulso de habilitación CP es 1 y la salida Q sigue los datos de entrada en tanto la señal CP permanezca en 1. Cuando CP pasa a 0, la información que estaba presente en la entrada de información precisamente antes de la transicion se retiene en la salida Q. En otras palabras, los flip-flop son sensitivos a la duración del pulso y el registro se habilita mientras CP=1. Un registro que responde a la duración del pulso en forma común se denomina compuerta con seguro y la variable de entrada se etiqueta como G (gate), los seguros son adecuados para utilizarse como almacenamiento temporal de información binaria que va a transferirse a un destino externo. No deben utilizarse en el diseño de circuitos secuenciales que tienen conexiones de retroalimentación.
Registro de carga paralela: La transferencia de información nueva a un registro se conoce como cargar el registro. Si todos los bits del registro se cargan en forma simultanea con un solo pulso de reloj, se dice que la carga es en paralelo. Un pulso aplicado a la entrada CP del registro cargara las cuatro entradas en paralelo.
Registros de corrimiento.
Un registro capaz de correr su información binaria ya sea a la derecha o a la izquierda se denomina
registro de corrimiento la configuración logica de un registro de corrieminto consta de una cadena de flip-flop conectados en cascada, con la salida de un flip-flop conectada a la entrada del siguiente flip-flop. Todos los flip-flop reciben un pulso común de reloj que causa el corrimiento de una etapa a la siguiente.
Transferencia serial: Se dice que un sistema digital opera en forma serial cuando la información se transfiere y se manipula un bit a la vez. El contenido de un registro se transfiere a otro corriendo los bits de un registro a otro. La información se transfiere un bit a la vez corriendo los bits de fuera del registro fuente del destino.
Registro de corrimiento bidireccional: Los registros con corrimiento pueden usarse para convertir datos seriales en datos en paralelo y viceversa. Si se tiene acceso a todas las salidas flip-flop de un registro con corrimiento, entonces la información que se introduce de manera serial por corrimiento puede tomarse en salida en paralelo mediante las salidas de los flip-flop. Si se agrega la capacidad de carga en paralelo a un registro con corrimiento, entonces la información que se introduce en paralelo puede tomarse en salida
en forma serial corriendo la información almacenada en el registro.
Adición serial: Las operaciones en las computadoras digitales se hacen principalmente en paralelo debido a que es el modo de operación mas rápido. Las operaciones seriales son lentas pero requieren menos equipo.
Contadores.
Los contadores MSI se dividen en dos categorías:
Contador binario de ondulación: este contador consta de una conexión en serie de flip-flop complementarios tipo C o JK, con la salida de cada flip-flop conectada a la entrada CP del siguiente flip-flop de orden mas alto. El flip-flop que retiene el menos significativo recibe los pulsos de acarreo que llegan. Un contador con un conteo en reversa se conoce como contador binario de decremento el conteo binario se disminuye en 1 con cada pulso de entrada de conteo. el conteo de un contador de decremento de 4 bits principia en el binario 15 y continua al conteo binario 14,13,12,...0 y entonces regresa a 15.
Contador de ondulación BCD: Un contador BCD cuenta en código decimal binario desde 0000 a 1001 y da vuelta a 0000. Debido al retorno a 0 despues de una cuenta de 9, un contador BCD no tiene un patrón regular como una cuenta binaria directa. Los contadores BCD pueden configurarse en cascada para formar un contador para números decimales en cualquier longitud.
CECyTE O5 ETC
50
Descargar
| Enviado por: | Gerry |
| Idioma: | castellano |
| País: | México |
