Física
Elasticidad de resortes
ELASTICIDAD DE UN RESORTE
INTRODUCCION
En el siguiente informe hemos pretendido hallar experimentalmente la constante de elasticidad de un resorte, el modulo de rigidez, para lo cual hacemos uso de la ley de Hooke y de las ecuaciones de Movimiento Armónico Simple de un resorte sometido a un esfuerzo para lo cual hemos usado resortes de diferentes constantes elásticas, puesto que también trabajamos con un resorte muy rígido el cual nos ocasiono muchas dificultades pero todos los resortes eran del mismo material (acero).
Para poder encontrar la constante de rigidez del resorte hemos aplicaremos dos métodos: El método estático y el método dinámico esta practica de laboratorio se desarrollo en dos semanas con la finalidad de poder comprender mejor los objetivos de la práctica, la primera semana trabajamos con el método estático método con el cual no tuvimos ningún inconveniente, la segunda semana hemos trabajado con el método dinámico, siendo este método el que nos ocasiono ciertas dificultades por la rigidez de uno de los resortes trabajados, lo cual nos revelara algunos errores de cálculo, errores que haremos notar en nuestras conclusiones.
Sin mas preámbulos pasamos al desarrollo de nuestro informe de laboratorio esperando sea del agrado de nuestro docente del curso.
OBJETIVOS
-
Usar un resorte como dispositivo para medir fuerzas.
-
Verificar experimentalmente las condiciones que cumplen las fuerzas que actúan sobre un cuerpo cuando éste esta en equilibrio.
-
Con un ejemplo sencillo, apreciar la importancia de los conceptos de fuerza y equilibrio en ingeniería.
FUNDAMENTO TEORICO
-
Elasticidad
Propiedad de un material que le hace recuperar su tamaño y forma original después de ser comprimido o estirado por una fuerza externa. Cuando una fuerza externa actúa sobre un material causa un esfuerzo o tensión en el interior del material que provoca la deformación del mismo. En muchos materiales, entre ellos los metales y los minerales, la deformación es directamente proporcional al esfuerzo. Esta relación se conoce como ley de Hooke. No obstante, si la fuerza externa supera un determinado valor, el material puede quedar deformado permanentemente, y la ley de Hooke ya no es válida. El máximo esfuerzo que un material puede soportar antes de quedar permanentemente deformado se denomina límite de elasticidad.
-
Ley de Hooke
Establece que dentro de los límites elásticos, la fuerza deformadora F y el valor de la deformación x, son directamente proporcionales:
…………. (1)
Donde k es una constante de proporcionalidad llamada constante elástica o constante de fuerza del resorte.
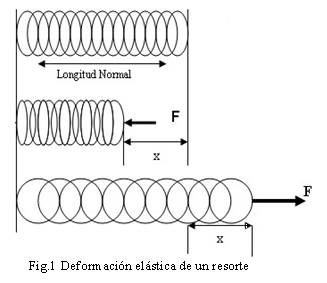
La deformación llamada también elongación es el estiramiento del resorte respecto de la posición de equilibrio (posición del resorte sin aplicar ninguna fuerza). De la ecuación (1) se tiene:
………….. (2)
La ecuación tiene la forma de la ecuación de la recta . Si hacemos las siguientes sustituciones: , entonces la pendiente B de la recta F VS X, representa a la constante elástica del resorte, k.
La reacción a la fuerza deformadora (fuerza externa), es la fuerza interna denominada fuerza restauradora o fuerza elástica del resorte Fs, la cual es de la misma magnitud que la fuerza deformadora. Esto es, ![]()
. Un cuerpo de masa “m” que se encuentra bajo la acción de una fuerza restauradora realiza un movimiento oscilatorio armónico simple cuyo periodo es:
…………. (3)
Esta ecuación también puede rescribirse de la siguiente manera:
……….. (4)
Que tiene la forma de la ecuación de la recta: . Si hacemos las sustituciones , la pendiente de la recta T Vs es:
![]()
………….. (5)
Cuando el resorte se estira por efecto de una fuerza de tracción, aumenta la separación entre sus espiras sucesivas de modo que el esfuerzo que soporta es, en realidad, un esfuerzo cortante o de cizalladura, tal como se ilustra en la fig.2.
La teoría respectiva permite relacionar al módulo elástico de rigidez o de cizalladura G del material, con la cortante elástica del resorte k del siguiente modo:
![]()
…………. (6)
Donde N es el numero de espiras del resorte, Res el radio de las espiras y r el radio del alambre.
MATERIALES E INSTRUMENTOS

-
2 resortes de acero
-
Pesas (500g, 1000g,)

-

1 soporte universal
-

Regla
-
Transportador
PROCEDIMIENTO Y DATOS EXPERIMENTALES
-
USO DE UN RESORTE PARA MEDIR FUERZAS:
-
Disponer las varillas y un resorte como se muestra en la figura.
-
Medir la longitud de resorte en la posición mostrada.
-
Colgar del extremo inferior de resorte sucesivamente pesas de 500 g, 1000 g y 770 g.
-
En un papel milimetrado graficar fuerzas (N) versus elongación del resorte (cm), en este grafico es lo que llamaremos curva de calibración del resorte.
-
Repetir los pasos anteriores para cada uno de los otros resortes.. identifique cada resorte con su respectiva curva de calibración.
Procedimiento:
Medir la longitud inicial L0 de referencia que podría ser la longitud original del resorte y la masa de las pesas.
Resorte Nº1
| N | m (Kg.) | F (N) | L (m) | ΔL (m) | |||||
| 1 | 0.500 | 4.900 | 0.240 | 0.110 | |||||
| 2 | 0.770 | 7.546 | 0.295 |
||||||
| Enviado por: | Aliwc |
| Idioma: | castellano |
| País: | Perú |