Matemáticas

Ecuaciones integrales

Compartir 0 Me sirvió 0 No me sirvió

Universidad “Gran Mariscal De Ayacucho”

Escuela De Ingeniería De Sistema

Cátedra: Matemática II

'Ecuaciones integrales'

Alumno:

Oleada Albert

C.I:18.012.600

Facultad:

Ing. Sistemas

Ciudad Bolívar 10 Octubre del 2006

INDICE

Introducción……………………………………………………………………………..03

INTRODUCCIÓN AL TEMA

Desarrollo…………………………………………………………………………….…04-27

FUNCION PRIMITIVA DE UNA FUNCION.

PROP. DE LAS PRIM. DE UNA FUNC.

INTEGRAL INDEFINIDA DE UNA FUNC

INTEGRALES INMEDIATAS

MÉTODOS DE INTEGRACIÓN ( I ).

Integración por cambio de variable (o sustitución).

MÉTODOS DE INTEGRACIÓN ( II ).

Conclusión…………………………………………………………………………………28

INTRODUCCION

Hasta ahora he aprendido las reglas de derivación y algunas de sus aplicaciones.

He tenido en cuenta que cuando se invierte algo donde intervienen más de una operación, éstas ha de invertirse pero en orden opuesto. Por aclarar esto, si consideras la operación de ponerte el calcetín y después el zapato, lo inverso será primero quitarte el zapato y luego una camisa. Cuando tenemos xn, al derivar multiplicamos por el exponente y luego disminuimos éste en una unidad, lo inverso será, primero aumentar el exponente en una unidad y después dividir por el exponente.

FUNCIÓN PRIMITIVA DE UNA FUNCIÓN

Dada una función cualquiera f(x) definida en un intervalo cerrado [a,b], se llama función primitiva de f(x) a otra función F(x) cuya derivada sea f(x) en dicho intervalo. Es decir, F'(x) = f(x) para todo x de [a,b].

Así:

La función sen x es una primitiva de cos x puesto que (sen x)' = cos x.

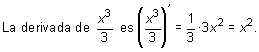
'Ecuaciones integrales'

PROP. DE LAS PRIM. DE UNA FUNC.

Primera propiedad

Si F(x) es una primitiva de f(x) y C una constante cualquiera (un número), la función

F(x) + C es otra primitiva de f(x).

Demostración:

Basta recordar que la derivada de una suma de funciones es igual a la suma de las derivadas de las funciones, y que la derivada de una constante es siempre cero.

(F(x) + C)' = F'(x) + C' = f(x) + 0 = f(x)

Ejercicio: primitivas de una función

ððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððððð

ð Encontrar tres primitivas de la función cos x.

Resolución:

ð Se sabe que sen x es una primitiva de cos x.

ð Tres primitivas de cos x son, por ejemplo,

Segunda propiedad

Si una función tiene una primitiva, entonces tiene infinitas primitivas.

Demostración:

Si F(x) es una primitiva de f(x), para cualquier constante C, F(x) + C es otra primitiva según la anterior propiedad. Así, hay tantas primitivas como valores se le quieran dar

a C.

Tercera propiedad

Dos primitivas de una misma función se diferencian en una constante. Esto es, si F(x) y G(x) son primitivas de la función f(x), entonces F(x) - G(x) = C = cte.

Demostración:

Hay que recordar que si una función f(x) definida en un intervalo cualquiera tiene derivada cero en todos los puntos, entonces la función f(x) es constante. Es decir, si f'(x) = 0, entonces f(x) = C.

Pues bien, si F(x) es una primitiva de f(x), F'(x) = f(x);

si G(x) es otra primitiva de f(x), G'(x) = f(x).

Restando miembro a miembro, F'(x) - G'(x) = (F(x) - G(x))' = f(x) - f(x) = 0, de donde se deduce que F(x) - G(x) = C.

INTEGRAL INDEFINIDA DE UNA FUNC.

Se llama integral indefinida de una función f(x), al conjunto de todas las primitivas de la función f(x), y se simboliza

Esta expresión se lee «integral de efe de equis diferencial de equis».

Por las propiedades de la función primitiva, si F(x) es una primitiva de f(x),

donde C representa una constante llamada constante de integración.

Ejercicio: cálculo de primitivas

Resolución:

ð Puesto que una primitiva de cos x es sen x,

Resolución:

Por consiguiente,

Resolución:

INTEGRALES INMEDIATAS

De la derivación de funciones elementales se deducen sus correspondientes integrales llamadas inmediatas. Es necesario aprender estos resultados si se pretende ser ágil en el cálculo de otras integrales menos sencillas.

Ejercicio: cálculo de integrales inmediatas

Resolución:

ð Es una integral inmediata perteneciente al segundo caso, en el que m = 4.

Resolución:

Resolución:

ð Por la propiedad del producto de potencias de la misma base,

Por tanto,

Resolución:

ð Es una integral inmediata perteneciente al cuarto caso en el que a = 3.

ð Comprobar la veracidad del vigésimo caso de integral inmediata.

Resolución:

ð Hay que probar la certeza de la igualdad

Basta demostrar que la derivada de la función

cociente,

Así,

'Ecuaciones integrales'

Se concluye que

'Ecuaciones integrales'

Por consiguiente,

MÉTODOS DE INTEGRACIÓN ( I )

Integración por descomposición

Este método se basa en la aplicación de dos propiedades elementales de las integrales:

ð Primera propiedad de las integrales

La integral de una suma (respectivamente diferencia) de funciones, es igual a la suma (respectivamente diferencia) de las integrales de las funciones.

Esto es,

Demostración:

Entonces, F(x) + G(x) es una primitiva de f(x) + g(x) y F(x) - G(x) es una primitiva de

f(x) - g(x), ya que:

(F(x) + G(x))' = F'(x) + G'(x) = f(x) + g(x)

(F(x) - G(x))' = F'(x) - G'(x) = f(x) - g(x)

Por tanto,

Análogamente,

ð Segunda propiedad de las integrales

La integral del producto de una constante por una función, es igual al producto de la constante por la integral de la función.

Es decir,

Demostración:

Pero (k · F(x))' = k · F'(x) = k · f(x), lo que indica que k · F(x) es una primitiva de

k · f(x). Por tanto,

Ejercicio: cálculo de integrales aplicando el método por descomposición

Resolución:

son integrales inmediatas pertenecientes al segundo caso.

En la primera, m = 2, y en la segunda, m = 1.

Así,

Por consiguiente,

Resolución:

= - cos x - 3 In |cos x| + C

Resolución:

ð Desarrollando por la fórmula del cuadrado de un binomio:

ð Así,

Resolución:

(Obsérvese que ahora la variable es t y no x. Conviene acostumbrarse al manejo de cualquier variable aunque la más utilizada sea la x.)

ð Aplicando la propiedad distributiva del producto:

ð Entonces,

'Ecuaciones integrales'

Resolución:

ð Descomponiendo la fracción en suma de fracciones:

ð Por tanto,

Resolución:

'Ecuaciones integrales'

Integración por cambio de variable (o sustitución)

Name=1; HotwordStyle=BookDefault; Este método consiste en transformar la integral dada en otra más sencilla mediante un cambio de la variable independiente. Aunque algunos casos tienen un método preciso, es la práctica, en general, la que proporciona la elección del cambio de variable más conveniente.

Se comenzará por estudiar aquellas integrales que son casi inmediatas.

Si en lugar de x se tuviese una función u(x), x → u(x) → u(x)m , la regla de la cadena

Por tanto,

Como se ve, se ha escrito u en lugar de u(x) por simplificar la notación.

Ejercicio: cálculo de integrales inmediatas por cambio de variable

Resolución:

ð Sin embargo, en la integral no se tiene 2x sino x. Este contratiempo se

por la constante (en este caso 2) que falta.

Resolución:

Resolución:

ð Se multiplica y se divide por 3:

'Ecuaciones integrales'

Si en lugar de x se tuviese una función de x, u(x), la derivada de ln | u(x) |, por la regla de

Ejercicio: cálculo de integrales por cambio de variable

Resolución:

ð Se multiplica y se divide por 6:

Resolución:

Por tanto,

La derivada de ex es la propia función ex . Si en lugar de x se tuviese una función

u( x ), la derivada de eu( x ) por la regla de la cadena es eu( x ) · u' ( x ).

Por consiguiente,

MÉTODOS DE INTEGRACIÓN ( II )

Ejercicio: cálculo de integrales mediante cambio de variable

Resolución:

ð En primer lugar se saca de la integral la constante 5.

ð Se multiplica y se divide por 3:

Resolución:

ð Se multiplica y se divide por - 1.

Resolución:

ð Se multiplica y se divide por 2:

Haciendo un estudio análogo a los anteriores, se deduce que

La derivada de - cos x es sen x. Por la regla de la cadena, la derivada de - cos u es

u' · sen u. Análogamente, la derivada de sen u es u' · cos u.

Así se tienen

Ejercicio: cálculo de integrales

Resolución:

La primera de ellas significa sen (x · x · x), mientras que la segunda es (sen x) · (sen x) · (sen x).

ð Se saca el factor 5 de la integral.

ð Se multiplica y se divide por 3.

ð Como en casos anteriores es sencillo demostrar que:

Ejercicio: cálculo de integrales

Resolución:

ð Se saca de la integral la constante 13.

ð Se multiplica y se divide por 50:

Resolución:

ð Se multiplica y se divide por 3.

Resolución:

ð Se extrae la constante 3 de la integral.

Por la derivada de un cociente,

Si u es una función de x, derivando por la regla de la cadena la función sec u, se obtiene u' · sec u · tg u. Análogamente, la derivada de la función - cosec u es u' · cosec u · cotg u. Por tanto,

Ejercicio: cálculo de integrales

Resolución:

ðSe multiplica y se divide por 2:

Resolución:

ð Se multiplica y se divide por 2:

Resolución:

ð De los casos 14, 15 y 16 de integrales inmediatas se deducen, de forma similar a como se ha hecho en los casos anteriores, las siguientes integrales inmediatas por cambio de variable:

Ejercicio: cálculo de integrales

Resolución:

Así, se ve claro que el cambio que se ha de efectuar es:

Resolución:

ð Se multiplica y se divide por 3:

Resolución:

ð Esta integral, aparentemente, no pertenece a ninguno de los tres casos, aunque tiene cierto parecido a una integral del primer caso.

'Ecuaciones integrales'

La técnica utilizada para resolver esta integral es de uso frecuente en el cálculo de integrales de cualquiera de estos tres modelos que se están estudiando.

Resolución:

ð Siguiendo los pasos del anterior ejercicio:

'Ecuaciones integrales'

ð Esta integral pertenece al segundo de los dos casos. El cambio que se

'Ecuaciones integrales'

Resolución:

lugar a una integral del tercer caso:

'Ecuaciones integrales'

Por tanto, es necesario multiplicar y dividir por 3.

'Ecuaciones integrales'

ð De los casos 17, 18, 19, y 20 de integrales inmediatas se obtienen las siguientes integrales inmediatas por cambio de variable:

MÉTODOS DE INTEGRACIÓN ( III )

Ejercicio: cálculo de integrales

Resolución:

ð Esta integral pertenece al tercero de los casos. Basta escribir 6x2 - 1 de forma adecuada: 6x2 - 1 = (
x)2 - 1

Resolución:

ð Escribiendo 25 x2 en la forma (5x)2, el cambio a efectuar es u = 5x; u' = 5.

ð Se multiplica y se divide por 5.

Resolución:

ð Transformando adecuadamente 4 - x2, esta integral es del cuarto tipo:

'Ecuaciones integrales'

Se estudia aquí esta integral por resolverse mediante un cambio de variable y por su frecuente uso en el cálculo de áreas y volúmenes mediante integrales definidas, que se estudiarán más adelante.

se hace uso del cambio de variable, x = a · sen t.

Diferenciando, dx = a · cos t dt.

Así,

Por trigonometría se sabe que:

En consecuencia,

Recordando que sen 2 t = 2 sen t · cos t,

'Ecuaciones integrales'

Se llega, finalmente, a la siguiente igualdad:

'Ecuaciones integrales'

Ejercicio: cálculo de integrales

Resolución:

ð Cambio de variable:

x = 3 sen t

dx = 3 cos t dt

ð Se deshace el cambio:

'Ecuaciones integrales'

Resolución:

ð En este caso se aplicará directamente el resultado al que se llegó:

'Ecuaciones integrales'

CONCLUSION

Se trata de tener los instrumentos que necesitarás para aplicarlos en la integral definida. Por tanto esto consiste en una preparación que se valorará cuando culmine el proceso.

El concepto y propiedades de la integral indefinida, integrales inmediatas; método de integración por cambio de variable, integración por partes; integración de funciones trigonométricas sencillas; integración de funciones racionales sencillas.

Pero esto no quita valor al esfuerzo, aunque es simplemente operacional, que supone el aprendizaje del cálculo de integrales. “Muchas Gracias”

Descargar

Enviado por:	ALBERT
Idioma:	castellano
País:	Venezuela

Palabras clave:

Matemáticas Ecuaciones integrales Integrales indefinidas Integrales inmediatas Métodos de integración Cambio de variable Cálculo de integrales Ejercicios de matemáticas

Te va a interesar