Ingeniero Químico
Ecuaciones de estado
Ecuaciones de estado
Una ecuación de estado exacta, que es una representación analítica del comportamiento ![]()
, frecuentemente es deseable desde un punto de vista computacional. Se han desarrollado muchas ecuaciones de estado diferentes. La mayoría de ella son exactas solo hasta una cierta densidad menor que la densidad critica, aunque unas pocas son razonablemente exactas hasta aproximadamente 2.5 veces dicha densidad critica. Todas las ecuaciones de estado resultan ser muy inexactas cuando la densidad excede la densidad máxima para la que se obtuvo la ecuación.
Pueden identificarse tres amplias clasificaciones de ecuaciones de estado, a saber, generalizadas, empíricas y teóricas.
La mas conocida de las ecuaciones de estado generalizadas es tambien la mas antigua, a saber, la ecuación de van der Waals, que fue presentada en 1873 como un perfeccionamiento semiteorico de la ecuación de gas ideal. La ecuación de estado de van der Waals es:
![]()
La constante b es la corrección por el volumen ocupado por las moléculas, y el término ![]()
es una corrección que toma en cuenta las fuerzas de atracción intermolecular. Como podría esperarse en el caso de una ecuación generalizada, las constantes a y b se evalúan a partir del comportamiento general de los gases. En particular estas constantes se evalúan observando que la isoterma critica pasa por un punto de inflexión en el punto critico, y que la pendiente es cero en ese punto. Por tanto, para la ecuación de van der Waals tenemos:
![]()
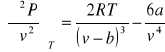
Puesto que ambas derivadas son iguales a cero en el punto crítico podemos escribir:
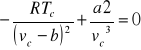
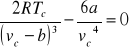
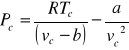
Resolviendo estas tres ecuaciones se halla que:
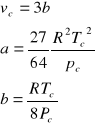
El factor de compresibilidad en el punto critico para la ecuación de van der Waals es:
![]()
que es mayor que el valor real para casi todas las circunstancias.
La ecuación de van der Waals puede escribirse en términos del factor de comprensibilidad y la presión y temperatura reducidas como sigue:

Es significado observar que esta es de la misma forma que el diagrama de compresibilidad generalizado, a saber, ![]()
, aunque la relación funcional pueda ser completamente diferente del diagrama generalizado. Este concepto de que sustancias diferentes tendrán el mismo factor de compresibilidad a la misma presión y temperatura reducidas, es otra manera de expresar la regla de estados correspondientes.
Una de las ecuaciones de estado empíricas mas conocidas es la ecuación de Beattie-Bridgeman, que es una ecuación explicita en P con cinco constantes que se determinan gráficamente a partir de datos experimentales para cada sustancia. Esta ecuación se introdujo en el capitulo 3 en la forma:
![]()
donde

Esta ecuación puede escribirse también en la forma:
![]()
donde

La tabla da los valores de las cinco constantes para varias sustancias. La ecuación de estado de Beattie-Bridgeman es completamente exacta para densidades menores que aproximadamente 0.8 veces la densidad crítica.
Muchas ecuaciones de estado empíricas se han desarrollado y utilizan para representar el comportamiento según ![]()
de diversas sustancias.
Un enfoque diferente para este problema es desde el punto de vista teórico. La ecuación de estado teórica, que se deduce a partir de la teoría cinética de los gases o de la termodinámica estática, se presenta aquí en forma de una serie de potencias del protocolo del volumen.
![]()
Donde B, C, D son cantidades dependientes de la temperatura y se llaman coeficientes viriales. B recibe el nombre de “segundo coeficiente virial” y se debe a intersecciones binarias a nivel molecular. Los coeficientes viriales pueden expresarse en términos de fuerzas intermoleculares de la mecánica estática y se evalúan después de seleccionar un modelo de función potencial empírico. Para todas las funciones excepto las mas simples, las expresiones matemáticas llegan a ser tan complejas que muy pocas se han llevado mas allá del Server coeficiente virial. Cuando la ecuación virial se utiliza con el segundo y tercer coeficientes viriales, el comportamiento según ![]()
se representa exactamente para densidades hasta de 0.7 veces la densidad critica.
El diagrama generalizado para cambios de entalpía a temperatura constante
En la sección 12.5 se dedujo la ecuación 12.33 para el cambio de entalpia a temperatura constante:

Una ecuación similar para el cambio de entalpía en un proceso isotérmico puede desarrollarse como sigue:

Sustituyendo una de las relaciones de Maxwell, ecuación 12.13, tenemos:
![]()
por tanto,

Un punto especial acerca de estas dos ecuaciones para ![]()
es que el cambio de entalpía a temperatura constante es función del comportamiento según ![]()
del gas. Esto significa que si la ecuación de estado se conoce para una sustancia, el cambio de entalpía a temperatura constante se puede determinar por la derivación e integración apropiadas. También se deduce que, siendo el diagrama generalizado una representación del comportamiento según ![]()
del gas, este diagrama puede utilizarse para formar un diagrama generalizado para el cambio de entalpía en un proceso isotérmico.
El procedimiento para el desarrollo de tal diagrama es como sigue:
se ha demostrado que,
![]()
pero
![]()
![]()
por consiguiente,

pero ![]()
y ![]()
. Por tanto,
![]()
![]()
![]()
![]()
sustituyendo estos valores tenemos


Integrando a temperatura constante se tiene,

Indiquemos por un símbolo con asterisco, h*, la entalpía por mol a una temperatura y una presión muy baja dadas, de modo que ![]()
e indiquemos sin índice superior la entalpía en un estado cualquiera a la misma temperatura y a una presión dada ![]()
Entonces la integración es como sigue:

el segundo miembro de esta ecuación se puede obtener por integración grafica del diagrama de compresibilidad y es funcion solo de la presion y la temperatura reducidas. El primer miembro representa el cambio de entalpía a medida que la presión aumenta desde cero hasta la presión dada si la temperatura se mantiene constante. A veces esta cantidad se llama desviación de entalpía. La figura B.9 muestra una grafica de esta cantidad ![]()
, como una función de ![]()
, para diversas líneas de ![]()
, constante.
En muchos casos se conoce el calor específico de una sustancia a baja presión. Esta información junto con el diagrama de entalpía residual generalizado, permite hallar el cambio de entalpía para cualquier cambio de estado dado.
Ejemplo 12.8
Se somete gas nitrógeno a un estrangulamiento desde 3000 ![]()
y -100 F hasta 200 ![]()
en un proceso adiabático EFE. Determínese la temperatura final del nitrógeno. El calor especifico a precion cero del nitrógeno en este intervalo de temperatura es de 0.248 ![]()
R. este es un proceso a entalpía constante (o isentálpico) y para resolver este problema tal como el de la figura 12.7
El diagrama generalizado para cambios de entalpía
Fig. 12.7 Croquis para el ejemplo 12.8
![]()
![]()

![]()
![]()
Del diagrama generalizado para cambio de entalpía a temperatura constante,
![]()
Btu/Ibmol R, ![]()
Btu/Ibm
Es necesario ahora suponer una temperatura final y comprobar, para ver si el cambio neto de entalpía para el proceso es cero. Supóngase que R. Luego el cambio de entalpía entre 1* y 2* puede hallarse a partir de los datos de calor especifico a presión cero.
Btu/lbm
(La variación de con la temperatura puede tomarse en cuenta cuando sea necesario.)
Hallaremos ahora el cambio de entalpía 2* y 2

Por tanto, el diagrama de desviación de entalpía, figura B.9,

Btu/lbmol R
![]()
Btu/lbm
Ahora comprobemos para ver si el cambio neto de entalpía para el proceso es cero.
![]()
=29.2+23.6+5.7=0.1 Btu/lbm
Esto comprueba esencialmente y se concluye que la temperatura final es aproximadamente de 265 R.
Fugacidad y diagrama de fugacidad generalizado
En esta parte se introducirá una nueva propiedad termodinámica, la fugacidad, f. Esta propiedad es particularmente importante cuando se consideran las mezclas y el equilibrio, que se estudian en el capitulo 14. Sin embargo, en vista de que puede desarrollarse un diagrama de fugacidad generalizado, se presenta ahora dicha fugacidad.
La fugacidad es esencialmente una seudo presión. Si la presión se sustituye por la fugacidad, es posible, en efecto, emplear las mismas ecuaciones para gases reales que normalmente se utilizan para gases ideales. El concepto de fugacidad puede introducirse como sigue:
Considérese la relación
![]()
A temperatura constante
![]()
Para un gas ideal esta última ecuación puede escribirse
![]()
(ln P)![]()
Y para un gas real, con la ecuación de estado ![]()
, esta ecuación se convierte en:
![]()
(ln P)![]()
La fugacidad, f, se define como:
![]()
(ln f )![]()
Se deduce de estas dos últimas ecuaciones que:
![]()
Puesto que ![]()
cuando ![]()
se deduce que:
![]()
Por tanto, cuando ![]()
![]()
.
Consideremos el cambio en la función de Gibbs de gas real durante un proceso isotérmico a la temperatura T que comprende un cambio de presión muy baja, ![]()
(donde puede suponerse comportamiento de gas ideal) hasta una presión mayor ![]()
. Desígnese la función de Gibbs a esta baja presión por ![]()
El valor de la función de Gibbs a esta temperatura T y a la presión ![]()
puede hallarse en términos de la fugacidad a la presión ![]()
y T y ![]()
. Esto es evidente si se integra la ecuación 12.65 desde la presión muy baja ![]()
hasta la presión ![]()
.
![]()
![]()
Un diagrama de coeficiente de fugacidad generalizado, basado en el diagrama de compresibilidad generalizado, figura B.10, puede desarrollarse por el siguiente procedimiento. Por las ecuaciones 12.62 y 12.65,
![]()
por consiguiente,
![]()
por lo tanto

Integrando a temperatura constante desde ![]()
hasta una presión finita tenemos que:

A cualquier temperatura el segundo miembro de esta ecuación puede ser integrado gráficamente utilizando el diagrama de compresibilidad generalizado para hallar Z en cada ![]()
el resultado es el diagrama generalizado que se muestra en la figura B.10.
El proceso isotérmico reversible es un tipo de problema en que la fugacidad puede ser utilizada ventajosamente.
Ejemplo 12.9
Calculase el trabajo de compresión y el calor transmitido por lbm cuando gas etano se comprime reversible e isotermicamente desde 14.7 lbf/![]()
hasta 1000 ![]()
a una temperatura de 110 F en un proceso EFE.
La primera ley para este proceso es:
![]()
puesto que el proceso es reversible e isotérmico,
![]()
por tanto

Supondremos que los cambios de energías cinética y potencial son despreciables.

![]()
Superficie de control
![]()
Fig. 12.8 Croquis para el ejemplo 12.9
La figura en el estado 1 y en el estado 2 puede se hallada a partir del diagrama de fugacidad generalizado del apéndice, figura B.10.
![]()
2
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | México |
