Matemáticas
Discontinuidades
DISCONTINUIDADES.CONTINUIDAD
La idea de función continua es la que “puede ser construida con un solo trazo”. Vamos a obtener algunos criterios mediante los cuales podamos saber si una función, dada por su expresión analítica, es o no continua
Discontinuidades
Razones por la que una curva no puede ser continua en un punto:
Tiene ramas infinitas en ese punto
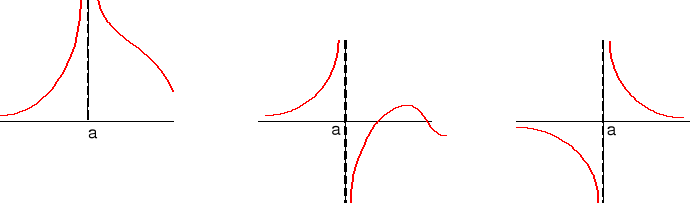
En estos casos, la recta se llama asíntota vertical de la curva.
Las funciones tienen una asíntota vertical en los valores de x para los cuales el denominador es cero
Presenta un salto en este punto
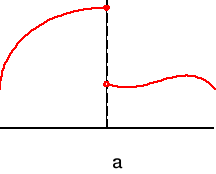
Le falta ese punto
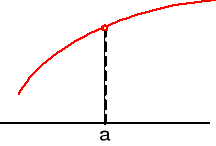
Tiene un punto desplazado
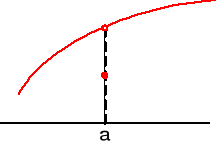
Relación de la continuidad en c con el límite cuando x tiende a c
Observando los distintos tipos de discontinuidad y el comportamiento de las funciones continuas, llegamos a la siguiente conclusión:
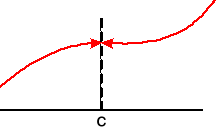
La función da un salto al llegar a la abcisa a. Entre las funciones elementales que nosotros manejamos, tal comportamiento solo se encuentra en funciones definidas a trozos
La función no está definida en la abcisa a, pero no tiene ramas infinitas ni presenta salto. Esta discontinuidad se llama evitable porque bastaría añadir ese punto para que la función fuera continua.
Este caso es como el anterior, pero la función si está definida en x=a, aunque el punto lo tiene desplazado. También este tipo de discontinuidad se llama evitable y solo puede conseguirse mediante funciones definidas a trozos
f es continua en si cumple las tres siguientes condiciones:
-
Tiene límite finito cuando :
-
Está definida en , esto es, f(c) existe
-
El límite coincide con el valor de la función en c:
Descargar
| Enviado por: | Koni |
| Idioma: | castellano |
| País: | España |
