Matemáticas
Circunferencia
CIRCUNFERENCIA
Definición. Se llama circunferencia al conjunto de puntos de un plano que se encuentran a la misma distancia de un punto fijo llamado centro.
Elementos:
-
Centro. Es el punto fijo que se encuentra a la misma distancia de cualquier punto de la circunferencia.
-
Radio. Es el segmento que une el centro con cualquier punto de la circunferencia, se representa por R o r.
-
Diámetro. Es el segmento que une dos puntos de la circunferencia y que pasa por su centro. El diámetro contiene a dos veces el radio.
-
Cuerda. Segmento que une dos puntos de la circunferencia.
La máxima cuerda es el diámetro.
-
Secante. Es una recta que corta a la circunferencia en dos puntos.
-
Arco. Un arco es una porción de la circunferencia comprendido entre dos Puntos
-
Tangente. Es una recta que tiene un punto común con la circunferencia. Al punto común se le llama punto tangente.
-
Flecha o Sagita. Segmento perpendicular a una cuerda en su su punto medio.
Propiedades Asociadas a los Elementos
-
El radio es perpendicular a la tangente.
-
Arcos comprendidos entre cuerdas paralelas son congruentes.
-
A arcos congruentes le corresponde cuerdas congruentes.
-
Un radio perpendicular a una cuerda, divide a la cuerda y al arco correspondiente en partes congruentes.
-
Por un punto exterior a una circunferencia sólo se puede trazar dos tangentes, estas tangentes son congruentes.
-
Tangentes comunes exteriores
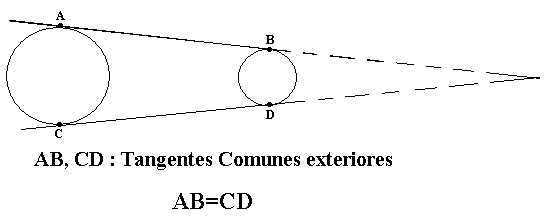
-
Tangente comunes interiores
Definición importante y teoremas
-
Circunferencia Inscrita:
Circunferencia inscrita en un triángulo es la circunferencia que es tangente a los tres lados. Al radio de esta circunferencia tambien se llama inradio.
-
La circunferencia es inscrita en el triangulo ABC.
-
El triángulo es circunscrito a la circunferencia.
-
r se llama inradio.
-
Cuadrilátero Circunscrito
Un cuadrilátero es circunscrito a una circunferencia cuando sus cuatro lados son congruentes a dicha circunferencia.
-
El cuadrilátero ABCD es circunscrito a la circunferencia.
-
La circunferencia es inscrita en el cuadrilatero ABCD
-
Teorema de Poncelet
En todo triángulo rectángulo, la suma de las longitudes de los catetos es igual a la longitud de la hipotenusa, más el doble del radio de la circunferencia inscrita.
-
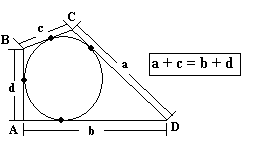
Teorema de Pitot
En todo cuadrilátero circunscrito a una circunferencia, la suma de las longitudes de los lados opuestos, es igual a la suma de las longitudes de los otros dos lados opuestos.
-
Teorema de Steiner
En todo cuadrilátero exinscrito a una circunferencia, la diferencia de las longitudes de dos lados opuestos, es igual a la diferencia de las longitudes de los otros dos lados opuestos.
Ángulos en la Circunferencia
-
Angulo central
El vértice se encuentra en el centro de la circunferencia, sus lados son dos radios. La medida del ángulo central es igual a la medida del arco comprendido entre sus lados.
-
Ángulo inscrito
Su vértice se encuentra sobre la circunferencia, sus lados son dos cuerdas. La medida del ángulo inscrito es igual a la mitad de la medida del arco comprendido entre sus lados.
-
Ángulo seminscrito
El vértice se encuentra sobre la circunferencia, sus lados son una tangente u una cuerda. La medida del ángulo seminscrito es inscrito es igual a la mitad del arco correspondiente a la cuerda.
-
Ángulo exinscrito
Su vértice se encuentra sobre la circunferencia, este ángulo es el adyacente suplementario de un ángulo inscrito.
-
Ángulo interior
El vértice se encuentra en el interior de la circunferencia, sus lados son dos segmentos de cuerda. La medida del ángulo interior es igual a la semisuma de las medidas de los arcos comprendidos entre sus lados y las prolongaciones de los lados.
-
Ángulo exterior
Su vértice es exterior a la circunferencia, sus lados pueden ser dos secantes, una tangente y una secante o dos tangentes. La medida del ángulo interior es igual a la semidiferencia de las medidas de los arcos comprendidos entre sus lados.
EJERCICIOS
Los lados de un triángulo ABC miden AB =12, BC= 13, AC=15, la circunferencia inscrita es tangente a AB en D, a BC en E y a AC en F. calcular (AD)(BD)(CF)
Solución:
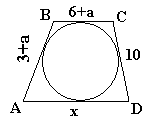
En un cuadrilátero ABCD circunscrito en una circunferencia se cumple que AB=3+a, BC= 6+a CD= 10 calcular AD
Solucion:
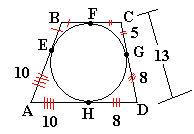
Encontrar AD, si FC = 5, CD = 13, AE = 10
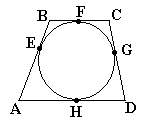
Solución:
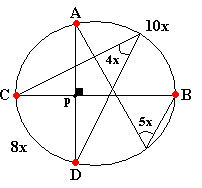
Encontrar x en :
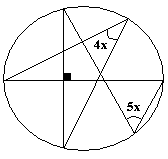
Solución:
En el paralelogramo ABCD calcular x
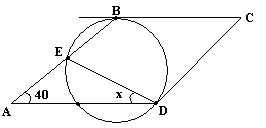
Solución:
En el cuadrante de centro O calcular “X”

Solución:
Como AO y OB son radios entonces AO=OB
Entonces trazo OC que también es radio:

Calcular x en:

Solución:
Calculando todos los datos de la figura se tiene:

El perímetro de un trapecio circunscrito a una circunferencia es 40, la distancia entre los puntos medios de las diagonales es 3. encontrar la longitud de la base mayor.
Solución:

Calcular BE en :

Solución: Encontramos datos en la figura:

-
Aplico T. de Pitot en el trapecio ABED:
12 + ED = x + x + m
ED = 2x + m ………….(1)
-
Aplico El T. de poncelet en el triángulo ECD
12 + m = ED + 2(2) …….(2)
ED = m+8
-
Igualo (1) y (2)
ED = ED
2x + m = m + 8
x = 10
Encontrar x en:

Solución: Encontrando datos en la figuara:

Del triangulo ABC se tienes que 50+X = 80
X = 30
Calcular X en:

Solución:

El lado AD del cuadrado ABCD es el diámetro de la semicircunferencia calcular x

Solución: extraemos datos de la figura

Calculo EC por T. de Pitágoras:
EC2 = BE2 + BC2
EC = 15
Aplico T. Poncelet en el triángulo BEC:_
BE + BC = EC +2x
9 +12 = 15 +2x
x = 3
BIBLIOGRAFIA
-
MATEMATICA 4, Manuel Coveñas Naquiche
Editorial Bruño
AD= P-BC
BE= P-AC P=(12+13+15)/2 = 20
CF= P-AB
Entonces:
AD= 20-13= 7
BE= 20-15= 5
CF= 20-12= 8
Entonces:
(AD)(BD)(CF) =7x5x8 = 280
Aplico teorema pitot:
AB+CD = BC+AD
3+a+10 = 6+a+x
x = 7
AD = 10+8
En el triángulo OCB:
50 + x + x = 180
2x = 130
x = 64
De la figura:
50 + 2x = 180
x = 65
Según datos:
-
a+b+c+x=40
-
(x-b)/2=3
x-b = 6
b = x - 6
-
Por T. de Pitot
a+b = b+x ……. Reemplazo en perímetro
a+b+c+x = 40
x= 13
Los arcos DE=FG
El angulo FEG = 65
Del triángulo se tiene:
X +65 = 90
X=25
Descargar
| Enviado por: | Jackson Garcia |
| Idioma: | castellano |
| País: | Perú |
