Electrónica, Electricidad y Sonido
Circuitos lógicos
Circuitos Lógicos, Álgebra de Boole y Dominios de Representación
Como se ha visto en los puntos anteriores, un computador es una serie de circuitos electrónicos que mediante el mecanismo de ejecución de instrucciones dan vida a una serie de operaciones que permiten, finalmente, ver lo que se ve al estar frente a la pantalla de uno de ellos y el poder interactuar, con ellos, de manera más o menos inteligente, dependiendo de lo que de ésta tenga el interactuante ya que se sabe que los computadores -como hoy se conocen- no tienen ni una pizca de inteligencia.
Básicamente un computador funciona mediante dos estados o valores conocidos como señales, por ejemplo, -1.5 volts y +4.0 volts. Estos voltajes tienen un significado lógico, con un valor se representa la existencia de una condición particular y el otro representa la ausencia de aquella condición.
Para aclarar los conceptos anteriores, considere algo en el mundo que sólo puede tomar dos estados o posiciones o características, por ejemplo, una puerta que sólo puede estar abierta o cerrada, o el día y la noche o lo que es más preciso si una luz está prendida o apagada. Los casos descritos, exageradamente, pueden tener esa condición dual que es posible representar por estas señales, por ejemplo la señal -1.5 volt podría representar a "la puerta abierta", "al día", "a la luz encendida" y en cambio la señal de +4.0 volt podría representar el otro estado de los hechos: "la puerta cerrada", "la noche", "la luz apagada".
Es decir, si se representa mediante estas señales el que una puerta esté cerrada o abierta, y se quiere saber cuál es la condición actual de la puerta, sólo se debe medir la señal: si ella tiene -1.5 volts entonces aquello significa que la puerta está abierta, en cambio, si ella estuviese cerrada, la señal que mediríamos sería la que corresponde a +4.0 volts.
Note que en los párrafos anteriores siempre se ha hablado de representar, esta acción es una de las piedras angulares de cualquier trabajo que se quiera hacer por medio de computadores. Para que se pueda representar es necesario que existan dos dominios, uno desde el cual se extraen los elementos que son usados para representar y, otro, de donde se distingue los elementos a representar. En el ejemplo anterior, el dominio que se usó para representar corresponde al dominio de las señales en el computador, en el cual existen dos elementos { -1.5 volts, +4.0 volts } y el dominio de los elementos a representar corresponde al de los estados de una puerta { "puerta abierta", "puerta cerrada" }.
Así la acción de representar es una que permite establecer relaciones entre estos dos dominios; lo que se hizo en el párrafo anterior al crear: ("puerta abierta", -1.5 volts) y ("puerta cerrada", +4.0 volts).
¿Por qué la representación resulta ser importante cuando se trabaja con computadores? Si se observa, mediante la representación anterior se relacionó un dominio básico del computador -el de las señales- y un dominio del mundo real -el estado de una puerta. Ahora, si esta puerta es la de la bóveda de un banco, esta representación por señales podría permitir saber si la puerta está abierta o cerrada sin necesidad de estar observándola directamente y, eso no es todo, dada esta posibilidad se podría pensar en determinar acciones considerando algunas condiciones que también es posible representar.
Por ejemplo, si se representa de la misma forma anterior los siguientes estados para el dominio de la bóveda { "bóveda vacía", "bóveda con gente" }, es decir, creando las relaciones ("bóveda vacía", -1.5 volts) y ("bóveda con gente", +4.0 volts). Así, se podría pensar en que es posible implementar un procedimiento como el siguiente:
Si está la "puerta abierta" y la "bóveda vacía" entonces realizar cerrar la puerta.
Que usando la representación definida, quedaría:
Si señal_puerta = -1.5 volts y señal_bóveda = -1.5 volts entonces realizar cerrar la puerta.
Cerrar la puerta sería la acción a realizar mediante un dispositivo automático o, si no existe tal dispositivo se podría avisar al guardia que lo haga, por ejemplo, prendiendo una luz en el tablero de la sala de guardias, la cual representa esa situación y la orden que un guardia vaya y cierre la puerta de la bóveda.
En el simplificado ejemplo anterior se tienen todos las características que permiten describir la solución de un problema mediante el uso de un computador -en este caso un dispositivo digital. Lo que primero se debe indicar son los dominios. En el dominio del problema se hace abstracción en muchos aspectos y, con ello, se identifican los objetos del problema; en este caso la puerta y sus estados { "puerta abierta", "puerta cerrada" } y la bóveda, también con sus dos estados { "bóveda vacía", "bóveda con gente" }.
Por otro lado existe el dominio de las señales del computador y sus dos estados { -1.5 volts, +4.0 volts } los que se utilizan para representar los objetos que se identifican en el problema, con ello se crea el dominio de las relaciones entre el dominio del problema y el dominio del computador, a este dominio se le llamará el dominio de las representaciones operacionales. Más adelante, en la segunda unidad 2, se profundizará más sobre este dominio.
Se observa que para el problema de la bóveda se realiza una acción que se denomina abstracción. Esta acción es tanto o más importante que la de representación. La acción de hacer abstracción consiste en preocuparse de una cosa y prescindir de las demás que están junto a ella. Un buen ejemplo de lo anterior, es que se prescindió de una serie de estados intermedios de abertura en la puerta y sólo se consideró los dos extremos. Del mismo modo no interesa la cantidad de gente que hay en la bóveda y las características que tiene ese tipo de gente, también se obvia todo lo que la bóveda es o tiene, sólo importa cuatro estados y la combinación de ellos, -(bóveda vacía, puerta abierta), (bóveda vacía, puerta cerrada), (bóveda con gente, puerta abierta), (bóveda con gente, puerta cerrada).
¿Por qué es necesario el hacer abstracción? Como se ha visto, el dominio de representación del ejemplo, sólo tiene dos estados posibles { -1.5 volts, +4.0 volts }, lo que lo hace un dominio sumamente simple. Frente a este dominio, la complejidad del mundo que rodea al problema de "cerrar la puerta de la bóveda" es inmensamente grande, hay miles de cosas que podrían ocurrir, por ejemplo: "Juan Pérez está entrando, en este instante, por la puerta de la bóveda en dirección de las cajas de valores clasificados, lleva una bolsita con $xxx.- en joyas correspondientes a diamantes y topacios.
El anda con la misma corbata amarilla que llevaba en la fiesta del fin de semana... etc. etc. etc." Hay un cantidad impresionante de objetos que no son necesarios para la solución del problema de "cerrar la puerta de la bóveda" y, además, dados los elementos que se posee para representarlos, sería imposible diseñar una solución "computacional" que considere todos aquellos elementos.
Para ello es necesario hacer abstracción: se debe reducir la complejidad del mundo-problema para poder representarlo y darle solución mediante el uso del computador.
Dominio Lógico
El funcionamiento del computador se basa en el dominio de las señales que se describieron en el ejemplo anterior, pero también un computador es mucho más complejo que aquellas señales, el sólo hecho de mirar la pantalla y ver la metáfora del mundo que aquella representa, hace surgir preguntas tales: ¿cómo funciona esto? O sí algo ya se sabe ¿cómo de un dominio tan pequeño, el de las señales, es posible obtener otro tan complejo como lo que se observa en la pantalla?
Para responder aquellas preguntas se debe partir desde el mismo dominio simple de los dos estado originales, el cual es posible representar por un conjunto de símbolos como { 0, 1 } o { V, F }, símbolos que describen a { -1.5 volts, +4.0 volts } respectivamente.
Pero se está frente a la misma situación anterior, sólo se ha cambiado la forma, pero ese conjunto de símbolos no tiene ninguna potencialidad, de ninguna forma es posible construir algo con aquellos símbolos.
Existe, en las matemáticas, un álgebra llamada Algebra de Boole. Fue desarrollada originalmente por George Boole, alrededor de 1850. La importancia de esta álgebra deriva de los trabajos de Claude Shannon en 1937, quién la utiliza para describir los circuitos digitales.
Un álgebra es posible definirla, muy simplificadamente, como un dominio en que además de un conjunto de elementos existe un conjunto de operadores u operaciones que permiten operar con aquellos elementos, generando elementos del propio dominio o de otros.
Así, el Algebra de Boole se describe como el siguiente dominio = ( { 0, 1 }, { And, Or, Not } ), donde el conjunto { And, Or, Not } corresponde al conjunto de operadores. Los símbolos con qué se representan estas operaciones son propios de esta visión simplificada del álgebra, ya que en el original son { ^, v, ~ } o desde el punto de vista del diseño de circuitos en ingeniería los símbolos que se utilizan son { ·, +, - }.
Otra propiedad de un Algebra es la utilización de variables que permiten representar, en general, cualquiera de los elementos del conjunto. Esta característica permite definir nuevas operaciones a partir de las originales o primitivas del álgebra. Así, una variable X definida sobre le Algebra de Boole puede tomar valores { 0, 1 }, por ejemplo X = 1, o X = 0. Para que sea más simple de entender se recomienda considerar 0 = falso y 1 = verdadero.
Operaciones Básicas
And. La operación And requiere que todas las señales sean simultáneamente verdaderas para que la salida sea verdadera. Así, el circuito de la figura necesita que ambos interruptores estén cerrados para que la luz encienda.
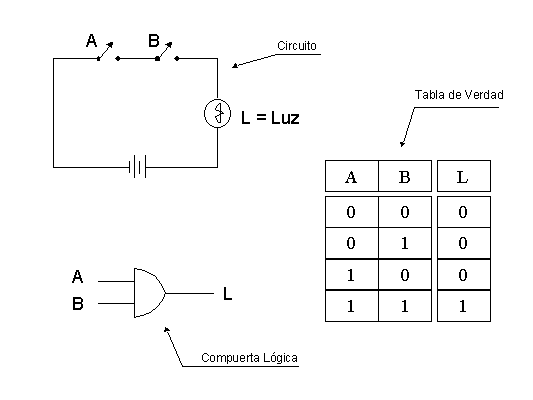
Figura No. 5. Operación And.
Los estados posibles del circuito se pueden modelar en la Tabla de Verdad que tiene asociada. Sabemos que los interruptores sólo pueden tener dos estados, abiertos o cerrados, si el interruptor abierto se representa mediante el cero (0 o falso) y el cerrado mediante el valor uno (1 o verdadero) entonces en la tabla de verdad asociada se puede ver la situación que se describía en el párrafo anterior, cuando se decía que la luz sólo prende cuando ambos interruptores están cerrados, es decir, si A = 1 y B = 1 entonces L = 1.
La compuerta lógica es una forma de representar la operación And pero en el ámbito de los circuitos electrónicos, para ese caso A y B son las señales de entrada (con valores = 0 1) y L es la señal de salida.
Para efectos de este curso, la operación And la representaremos como la función And( A, B ), donde A y B serían los parámetros de entrada (los mismos valores de A y B en el circuito) y L = And( A, B ), correspondería a la forma de asignación de valor a L. En este caso el parámetro de salida es la misma función And.
Or. La operación Or tiene similares características a la operación And, con la diferencia que basta que una señal sea verdadera para que la señal resultante sea verdadera. En la figura se puede ver tal situación.
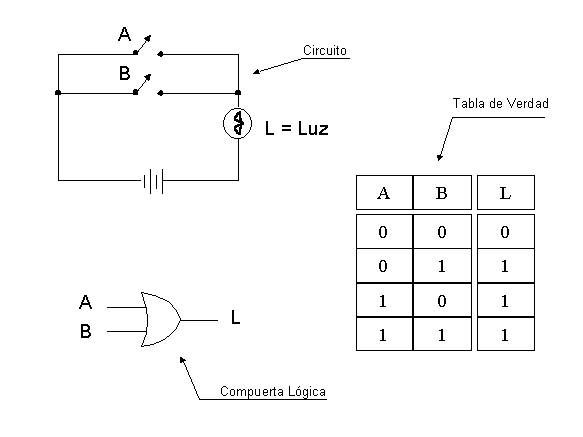
Figura No. 6. Operación Or.
Note que en el circuito los interruptores están en paralelo, por lo cual basta que uno de ellos esté cerrado para que el circuito se cierre y encienda la luz.
La operación Or también tiene una representación funcional como Or( A, B ) donde A y B serían los parámetros de entrada (los mismos valores de A y B en el circuito) y L = Or( A, B ), correspondería a la forma de asignación de valor a L. En este caso, el parámetro de salida es la misma función Or.
Not: La última de la tres operaciones fundamentales, la cual también se conoce como negación, complemento o inversión, es mucho más simple que las anteriores. En la figura se puede observar el circuito, que en este caso tiene la particularidad de que al estar el interruptor abierto la luz enciende, cuando él está en posición de cerrado la luz permanecería apagada.
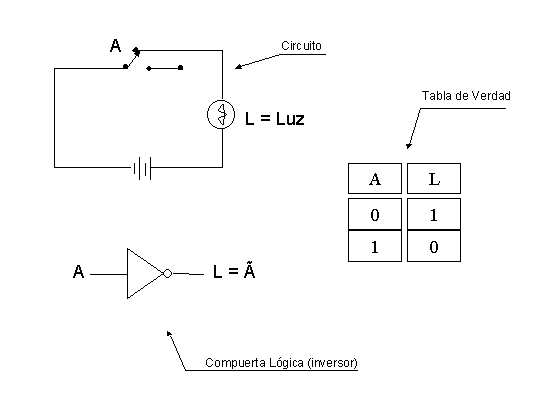
Figura No. 7. Operación Not.
La notación funcional para esta operación será Not( A ), donde A corresponde a la señal de entrada y Not( A ) corresponde al valor complementario de A.
Con las operaciones básicas ya definidas es posible redefinir el Algebra de una manera más formal, por ejemplo, dándole el nombre de Dominio Lógico y caracterizandolo de la siguiente manera:
Dominio Lógico ( l ð Dominio Lógico ) = ( { 0, 1 }, { l: And( l, l ), l:Or( l, l ), l:Not( l ) } )
Note que cada una de las operaciones o funciones de este dominio se ha explicitado claramente la cantidad y el tipo de parámetros con los cuales ellas operan (operandos) y el tipo de valor que la operación devuelve, en este caso todos los parámetros son del tipo lógico ( l ).
Así, cuando se habla del dominio del computador al resolver un problema, este dominio tiene como base el dominio recién descrito. Los circuitos electrónicos que dan vida al computador pueden ser representados todos mediante este Dominio Lógico.
Operaciones compuestas
El conjunto de las operaciones del dominio básico se puede extender mediante un mecanismo de composición de operaciones, por ejemplo, se quiere agregar la operación XOR, que corresponde a un OR Exclusivo mediante el cual: si ambas entradas son iguales el resultado es cero (0 o falso) y si ambas son distintas, entonces el resultado es uno (1 o verdadero). Graficamente se puede ver la implementación de la compuesta XOR en la figura No. 8.
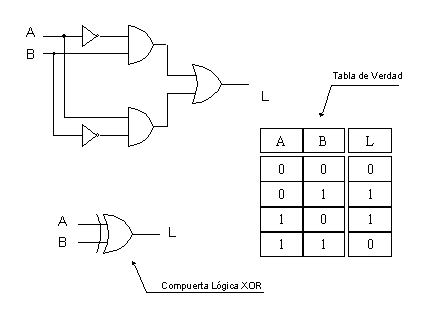
Figura No. 8. Implementación de la Compuesta XOR.
Es claro, en la figura, la forma de composición de la operación XOR a partir de las operaciones básicas and, or y not en el formalismo gráfico de las compuertas lógicas. También es posible usar el formalismo funcional, que se consideró en la definición el Domino Lógico, para componer la operación XOr:
Or( And( Not( A ), B ), And( A, Not( B ))); donde A, B ð Dominio Lógico
De hecho, si se quiere extender el conjunto de las operaciones del Dominio Lógico sería necesario expresar, la operación XOr, en el mismo formato que las operaciones primitivas; sin ser muy rigurosos bastaría con una asignación para que con ello se tenga una forma de definir nuevas operaciones en base a las ya existentes:
XOr( A, B ) ð Or( And( Not( A ), B ), And( A, Not( B ))) ; donde A, B, XOr ð Dominio Lógico
El símbolo ð permitiría trasladar toda la funcionalidad de la expresión a la nueva operación, incluidos los parámetros de entrada y salida (A, B como parámetros de entrada y el nombre de la operación XOr como parámetro de salida). Con la operación XOr ya definida es posible, entonces, ampliar la definición del Dominio Lógico:
Dominio Lógico ( l ð Dominio Lógico ) = ( { 0, 1 }, { l: And( l, l ), l:Or( l, l ), l:Not( l ) l:XOr( l, l ), } )
Por lo cual XOr podría ser utilizado para componer nuevas operaciones de este mismo dominio o, eventualmente, de otros.
Construcción de nuevos dominios
Pese a que se ha formalizado un dominio básico y, además, se ha creado nuevas operaciones dentro de ese dominio, aún no se cumple el objetivo de poder aproximar el mundo de señales del computador a nivel de complejidad actual observado.
En los puntos anteriores se revisó la forma de representación de los números enteros, la cual se basaba en una memoria organizada en palabras de 8 bits. Es decir, si se considera que cada una de las señales básicas puede ser utilizada para componer un bit, entonces sería necesario 8 señales para poder componer un número, donde cada una de estas señales podría tomar los dos estados posibles y, dependiendo de la posición en que ella esté -recuerden lo hablado sobre sistemas numéricos posicionales- tendría más o menos incidencia en el valor del número a representar, por ejemplo, el siguiente número binario, representa al 165 decimal -según la transformación estudiada:
xb = 10100101
X10 = V(xb) = 1× 27+0× 26+1× 25+0× 24+0× 23+1× 22+0× 21+1× 20 = 165
Con esta forma de representación es posible entonces sintetizar un conjunto de números enteros a partir de las señales originales, combinándolas. En este caso el conjunto de enteros puede ser uno que vaya desde 0 a 255, pero si se amplia el número de señales paralelas consideradas, este espectro se puede aumentar o, considerando el signo, se pueden incluir números negativos.
Así, para crear el conjunto de los números enteros a partir del conjunto de las señales se debe organizar éstas en cadenas paralelas -la forma usual de los buses dentro del computador- donde la posición de cada una tiene un peso específico en la síntesis del número que se está representando. En la notación que se está propugnando, un conjunto de estas cadenas puede ser visto de la siguiente forma:
Dominio Enteros Binarios ( nb Î Dominio Enteros Binarios) = ( { Ln...L7L6L5L4L3L2L1L0 / Li Î Dominio Lógico} )
Ahora, si bien existe una representación factible de números enteros a partir de las señales primitivas, un dominio de los enteros (que en este caso se ha denominado enteros binarios por no estar expresados en base decimal) no está completo si es que no existen operaciones que permitan manejarlos, por lo cual es necesario componer tales operaciones a partir de del dominio lógico o de las mismas operaciones ya desarrolladas para este dominio.
Suma en los enteros binarios
La suma de dos números binarios se realiza de la misma manera que la suma en los números decimales. Por ejemplo, la siguiente es una suma decimal:
3 7 6 los números en negrillas corresponden a los dígitos menos significativos
+ 4 6 1
8 3 1
Los dígitos en las posiciones menos significativos son operados primero, produciendo la suma 7. Luego, los dígitos en la segunda posición son sumados para dar el resultado 13, que produce un acarreo de 1 hacia la tercera posición, lo que produce la suma 8.
Los mismos pasos generales son seguidos en la suma binaria. Sin embargo, aquí sólo hay que considerar cuatro casos al sumar dos dígitos binarios:
0 + 0 = 0
1 + 0 = 1
1 + 1 = 0 + acarreo de 1 (uno) a la siguiente posición
1 + 1 + 1 = 1 + acarreo de 1 (uno) a la siguiente posición
El último caso ocurre cuando dos bit de una cierta posición tienen 1 (uno) y además hay un acarreo desde la posición previa. Los siguientes son varios ejemplos de sumas de dos números binarios:
011 (3) 1001 (9) 11,011 (3,375)
+110 (6) +1111 (15) +10,110 (2,750)
1001 (9) 11000 (24) 110,001 (6.125)
No es necesario considerar la suma de más de dos números binarios al mismo tiempo, ya que todos los sistemas de circuitos digitales que actualmente ejecutan la suma sólo pueden manejar dos números a la vez. La suma es una de las operaciones aritméticas más importantes en los sistemas digitales, de hecho, las operaciones de resta, multiplicación y división pueden ser definidas en base a la suma.
Si se quiere entonces sumar dos números enteros binarios en un computador, es necesario para ello que exista la operación suma de enteros binarios. De manera análoga a como se definió la operación XOr, es posible definir ahora una operación de suma.
La unidad aritmética
Todas las operaciones aritméticas se realizan en la unidad aritmética, también conocida como unidad aritmético-lógica -ver punto 1.2 de este apunte-, de un computador. La Figura No. 9 es un diagrama de bloques que describe los principales elementos incluidos en una unidad aritmética típica. El principal propósito de una unidad aritmética es aceptar datos binarios que están almacenados en memoria y ejecutar las operaciones aritméticas sobre aquellos datos de acuerdo a las instrucciones dadas desde la unidad de control.
La unidad aritmética tiene al menos dos registros de flip-flops: el registro B y el registro acumulador. Además contiene los circuitos lógicos que permiten ejecutar las operaciones sobre los números binarios almacenados en ambos registros. La típica secuencia de ejecución para una suma (ADD) puede ser la siguiente:
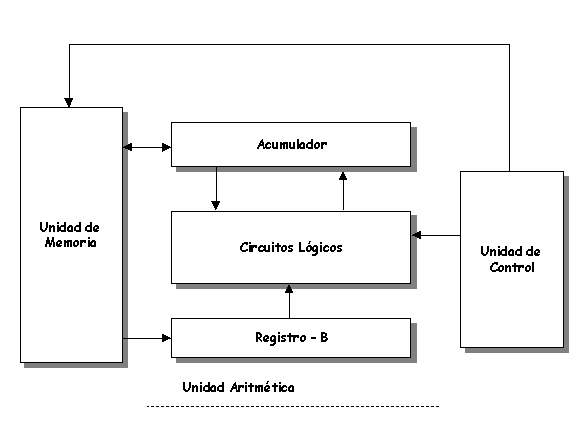
Figura No. 9. Unidad Aritmética
-
La unidad de control recibe una instrucción (desde la unidad de memoria) indicando que un número almacenado en una ubicación particular de memoria (dirección) deberá ser sumado a el número actualmente almacenado en el acumulador.
-
El número a ser sumado es transferido desde la memoria al registro B.
-
El número en el registro B y el número en el acumulador son sumados en los circuitos lógicos (comandados desde la unidad de control). La suma resultante en enviada al acumulador para ser almacenada.
-
Al nuevo número en el acumulador se le puede sumar otro, o si el proceso aritmético en particular ha terminado, el número puede ser transferido a memoria para almacenarlo.
Estos pasos demuestran de donde el registro acumulador deriva su nombre. Este registro "acumula" los valores que resultan de ejecutar sucesivas sumas entre nuevos números extraídos desde memoria y el resultado de las sumas anteriores almacenado en el acumulador. Para cualquier problema aritmético que contienen varios pasos, el acumulador siempre contiene el resultado de los pasos intermedios, así como el resultado final cuando la ejecución ha terminado.
Un sumador binario en paralelo
Los computadores y calculadoras implementan la operación de suma sobre dos números binarios al mismo tiempo, donde cada numero binario puede tener varios dígitos binarios. En la tabla se muestra la suma de dos números binarios de cinco bits. Uno de los operandos es almacenado en el acumulador; esto es, el acumulador contienen cinco Flip-Flops, almacenando, en cada uno, los dígitos 10101. De la misma forma el otro de los operandos, el que será sumado al primero, es almacenado en el registro B (en este caso, 00111).
El proceso de suma comienza por la suma de los bit menos significativos de ambos operandos. Así, 1+1 = 10, que significa que la suma para esa posición es 0 y el acarreo es 1.
| 1º Operando, almacenado en el acumulador | 1 | 0 | 1 | 0 | 1 |
| 2º Operando, almacenado en el Registro B | 0 | 0 | 1 | 1 | 1 |
| Suma | 1 | 1 | 1 | 0 | 0 |
| Acarreo (para ser agregado a la siguiente posición) | 0 | 0 | 1 | 1 | 1 |
Este acarreo (o bit de carry) será sumado a la siguiente posición, junto a los bit correspondientes de los operandos. Así, en la segunda posición 1+0+1 = 10, que corresponde nuevamente a la suma 0 y el carry 1. Este carry será sumado a la siguiente posición junto a los correspondientes bits de los operandos y así sucesivamente hasta las últimas posiciones.
A cada paso en el proceso de suma se realiza la adición de tres bits; los dos de los operandos y el de carry que viene de la posición previa. El resultado de la suma de estos 3 bits produce 2 bits: un bit de suma y otro de carry que deberá ser sumado a la siguiente posición. Este mismo proceso es usado para cada posición. Ahora, si se quiere diseñar un circuito lógico que permita implementar este proceso, entonces simplemente se deberá usar el mismo circuito para cada una de las posiciones. Esto se ilustra en la Figura No. 10.
En este diagrama las variables Ai representan los bits del operando almacenados en el acumulador (que también puede ser llamado el registro A). Las variables Bi representan los bits del segundo operando almacenados en el registro B. Las variables Ci representan los bits de carry entre las correspondientes posiciones. Las variables Si son los bits de la suma para cada posición.
Los circuitos Full-Adder usados en cada posición tienen tres entradas: un bit A, un bit B y un bit C; y producen dos salidas: un bit de suma (S) y un bit de carry (C). Por ejemplo, el Full-Adder No. 0 tienen como entradas A0, B0 y C0, y produce las salidas S0 y C1. Lo anterior se repite para todos los bits de los operandos. Actualmente los computadores usan palabras de 32 y 64 bits, al contrario del de la figura que sólo es un sumador de 5 bits.
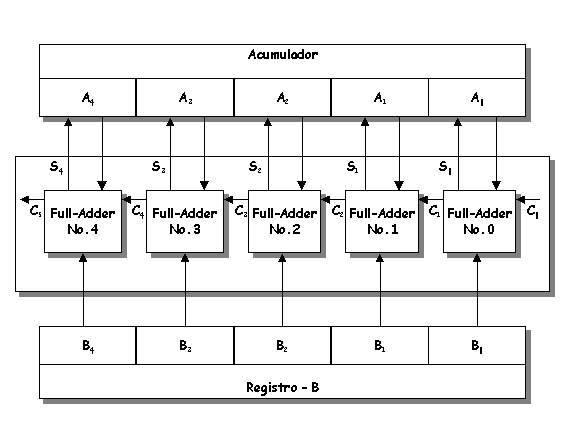
Figura No. 10. Diagrama de Bloques de un sumador paralelo de 5-bits usando full-adders.
El arreglo de la figura No. 10 se llama sumador paralelo (parallel adder) por que todos los bits de los operandos se usan simultáneamente en todos los circuitos. Esto significa que la suma en cada posición ocurre al mismo tiempo. Que es distinto de las sumas que se hacen en papel. Ya que se toma cada posición una a la vez, comenzando desde las posiciones menos significativas.
El diseño de un Full-Adder
El diseño de un Full-Adder es un típico problema de ingeniería -en este caso de electrónica- y resulta muy interesante y didáctico seguirlo paso a paso, se recomienda para ello consultar el libro "Digital Systems: Principles and Applications" de Ronald J. Tocci en las páginas 146 y 147.
Lo primero que se hará es construir una Tabla de Verdad que muestre los valores de entrada y salida para todos los casos (recuerde que sólo se intenta diseñar un Full-Adder). En la siguiente tabla se puede ver aquello, con tres entradas (A, B y Cin) y dos salidas (S y Cout). Existen ocho posibles casos para las tres entradas, y para cada caso se desea la salida listada en los valores de salida. Por ejemplo, considere el caso A = 1, B = 0, y Cin = 1. Un Full-Adder (que abreviaremos FA) puede sumar estos bits para obtener las salidas S = 0 y Cout = 1.
| A | B | Cin | S | Cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
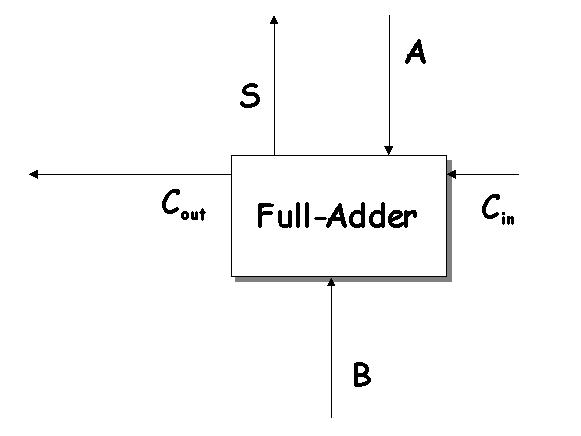
Como existen dos salidas, se puede diseñar el circuito por cada salida individualmente, comenzando con la salida de la suma S. Por la tabla de verdad se ve que hay cuatro casos donde S tiene valor 1. Si se compone una expresión para ello, usando el Dominio Lógico, y luego de refinarla, según un método que no es el caso desarrollar acá, se obtienen la siguiente expresión final:
S = Xor( A, Xor( B, Cin )) (a)
Si se considera ahora la salida Cout, también se puede componer una operación, en el dominio lógico, que permita realizarla:
Cout = Or( And( B, Cin ), Or( And( A, Cin ), And( A, B ))) (b)
Las expresiones a y b pueden ser implementadas como se muestra en la Figura No. 11, cada Full-Adder de la Figura No. 10 puede ser implementado según el circuito lógico que aparece en esta figura.
Para desarrollar este circuito en términos del formato que se ha estado propugnando para los dominios, es necesario ampliar a la capacidad de definición de operaciones. Para ello es necesario que las nuevas operaciones, además de permitir combinaciones directas de las ya definidas, permitan otro tipo de combinaciones con más poder de cómputo. Ese es el objetivo de los lenguajes de Programación, permitir ampliar la capacidad de definición de nuevos dominios y operaciones, de manera que esta ampliación permita ampliar a su vez el espectro de los problemas posibles de abordar mediante el uso de un computador.
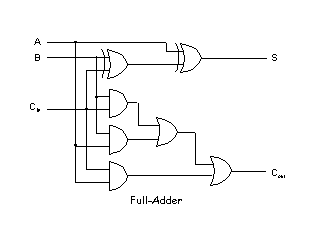
Figura No. 11. Circuito Completo para Full-Adders.
El PseudoLenguaje que se describe en el siguiente punto tiene la cualidad de permitir a quien lo ocupa ampliar su capacidad de resolver problemas mediante el uso de computador.
Descargar
| Enviado por: | Jamiro18 |
| Idioma: | castellano |
| País: | Chile |
