Física
Campo eléctrico
CAPITULO I : CAMPO ELECTRICO
CARGA ELECTRICA
La carga es una propiedad fundamental y característica de las partículas elementales que forman la materia.
La materia está formada por cantidades enormes de átomos y moléculas.
Todo átomo está constituido por un núcleo, en torno al cual giran partículas llamados electrones. El núcleo de un átomo está básicamente formado por protones y neutrones.
Los protones son partículas cargadas positivamente, mientras que los electrones lo son negativamente. Los neutrones son partículas sin carga.
Si la materia es eléctricamente neutra, esto se debe a que el número de protones en un átomo (Z) es igual al número electrones y la carga del electrón es igual a la carga del protón.
Desde el punto de vista macroscópico, la carga se refiere a la carga neta o al exceso de carga, cuando decimos que un objeto está cargado, lo que queremos decir es que tiene un exceso de electrones (cargada negativa) o un exceso de protones (cargado positivamente).
En un sistema cerrado, las cargas pueden reagruparse y combinarse en distintas formas; sin embargo, podemos establecer que la carga neta dentro de dicho sistema se conserva. Lo anterior constituye el principio de conservación de la carga.
Experimentalmente se ha encontrado que la carga se presenta en múltiplos de una cantidad fundamental, así:

lo que se conoce como “cuantización de la carga”
Uno de los muchos experimentos para demostrar esto es el ideado por Millikan (experimento de la gota de aceite). El estudiante puede encontrarlo en la mayoría de textos de Física General.
LEY DE COULUMB
Describe la interacción eléctrica entre dos partículas cargadas bajo las condiciones:
Las partículas cargadas se encuentran en reposo en el sistema inercial de referencia del observador o, cuando mas moviéndose a una velocidad muy pequeña.
Las cargas pueden considerarse “puntuales”
Las cargas se encuentran en el espacio libre (vacío)
El espacio libre se comporta como un medio homogéneo, isométrico y lineal.
Homogéneo: Las propiedades eléctricas no son función de la posición.
Isótropo: Las propiedades eléctricas no son función de la dirección que une las cargas.
Lineal: el factor de proporcionalidad K0, entre las causas y el efecto, debe ser constante sin importar la magnitud del fenómeno.
La ley de Coulumb nos dice:
“La interacción eléctrica entre dos partículas cargadas es proporcional a sus cargas e inversamente proporcional al cuadrado de la distancia entre ellas, y su dirección es según la recta que las une”
Expresada matemáticamente y en concordancia con la Fig. 01
En ejercicios de aplicación usaremos
Por razones prácticas y de cálculo numérico es conveniente expresar en la forma:
, Usaremos esto cuando sea necesario.
Donde es una nueva constante que llamaremos permitividad del vacío.
El lector puede verificar que (1) también podemos expresarlo asi:
Calculamos la fuerza sobre ![]()
, es decir , cambiando en (1) o en (2) cada subíndice i a j y cada j a i podemos mostrar de este modo que .
Dependiendo de que los signos de las cargas sean iguales u opuestos, estaos serán repulsivas o atractivas, respectivamente.
Si se considera un sistema de N cargas puntuales interactuando, la fuerza sobre la iésima carga, , está dada por la aplicación repetida de la ecuación (1) o (2), asi:
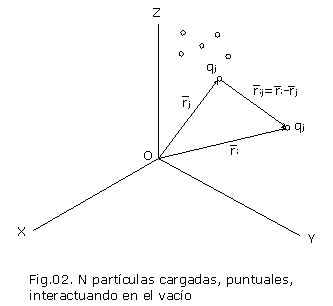
Notemos que la expresión (3) nos da la fuerza sobre una carga puntual , debido a su interacción con una distribución discreta de cargas. Ver fig.02.
FUERZA SOBRE UNA CARGA PUNTUAL DEBIDO A UNA DISTRIBUCIÓN DE CARGA CONTINUA: LINEAL, SUPERFICIAL Y VOLUMÉTRICA.
Esta es una simple extensión de la idea de N cargas puntuales interactuando. Tomando a como nuestra carga puntual y reemplazamos la sumatoria por una integral extendida a toda la distribución contínua así:
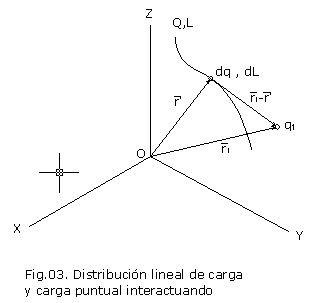
Las expresiones (4), (5) y (6) nos dan la fuerza sobre una carga puntual debido a su interacción con una distribución continua de carga: lineal, superficial y volumétrica respectivamente.
La variable r' se usa para localizar un punto en la distribución de cargas, esto es, hace el papel de en la ecuación (3), ver figuras 03,04 y 05.
CAMPO ELECTRICO DE UNA CARGA PUNTUAL
Observamos las ecuaciones (2), (3), (4), (5) y (6) notamos que la fuerza sobre una carga puntual ![]()
(que en adelante la denominaremos “carga testigo”) es proporcional a ![]()
, esta observación nos conduce a introducir un campo vectorial independiente de ![]()
, al cual denominaremos “Campo Eléctrico”.
Operacionalmente podemos definir la intensidad del campo eléctrico en un punto, como la fuerza por unidad de carga (testigo) colocada en ese punto asi:
El campo eléctrico lo expresamos, de acuerdo con la relación (7), en unidades de
Si usamos la ecuación (2), el campo eléctrico producido por una carga puntual (carga fuente) evaluando en el punto donde esté ubicada ![]()
, será:
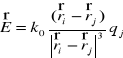
..... (8)
Si hacemos coincidir en la Fig 01, el origen O con el punto donde está ubicado la caraga , la expresión (8) se simplifica, obteniendo:
![]()
..... (9)
Ahora; ![]()
, y ![]()
, es el vector unitario en la dirección de ![]()
, ver Fig. 07
(b)
Fig. 07. orientación del campo eléctrico producido por una carga puntual a) positiva y b) negativa.
CAMPO ELECTRICO DE UNA DISTRIBUCIÓN DISCRETA DE CARGAS
Siguiendo el mismo criterio adoptado en la sección anterior, el campo eléctrico producido por una distribución discreta de cargas (cargas puntuales), a partir de la ecuación (3), será:

.... .(10)
Esta ecuación nos da el campo eléctrico producido por todas las cargas (excepto qi) en la posición en que está ubicada qi.
En este caso, qi es la carga testigo y todas las cargas que producen el campo, las cargas fuente.
CAMPO ELECTRICO DE UNA DISTRIBUCIÓN CONTINUA DE CARA: LINEAL, SUPERFICIAL Y VOLUMÉTRICA
La generalización a los casos en que el campo eléctrico es producido por una distribución continua de carga es inmediato, reemplazando en la expresión (10) la sumatoria por una integral, de acuerdo a la distribución que se trate:

..... (11)
..... (12)
..... (13)
Las ecuaciones (11), (12) y (13), nos dan el campo eléctrico producido por una distribución continua, lineal, superficial y volumétrica, respectivamente, evaluados en la posición donde está ubicado qi. Una vez más hacemos notar que la variable ![]()
, se usa para localizar un punto en la distribución de carga y ![]()
, es el vector de posición del punto donde estamos evaluando el campo (o donde esta ubicado la carga testigo qi).
De lo expuesto concluimos que, cualquier región del espacio en donde una carga eléctrica (carga testigo qi) experimenta una fuerza, se llama campo eléctrico. La relación entre el campo eléctrico y la fuerza sobre la carga ubicada en ese punto, en todos los casos descritos será:
![]()
..... (14)
De tal manera que, si qi es positivo, la fuerza que actúa sobre la carga es paralela al campo eléctrico y antiparalelo si qi es negativo.
Por tanto, si aplicamos un campo eléctrico en una región donde haya iones positivos y negativos, el campo tenderá a mover los cuerpos cargados en direcciones opuestas, según que sean las cargas positivas o negativas, lo cual da como resultado una separación de cargas, efecto éste llamado polarización (ver Fig. 08)
Fig 08. Separación de cargas de signos opuestos por una campo eléctrico.
LEY DE GAUSS EN FORMA INTEGRAL
Consideremos una carga o, si se quiere, un sistema de cargas puntuales, positivas o negativas, encerradas por una superficie cerrada de forma arbitraria, como se muestra en la Fig. 09.
La ley de Gauss en forma integral establece que:
“ El flujo eléctrico que pasa a través de cualquier superficie cerrada es proporcional a la carga total encerrada por esa superficie”
Si el medio es el vacío, la constante de proporcionalidad es ![]()
.
Expresada en forma integral:
![]()
..... (15)
En la ecuación (15), la sumatoria sobre las N cargas se hace considerando el signo positivo o negativo de cada una de ellas.
Esto conduce a utilizar el término de carga neta, pero, aquí conservaremos el término de carga total.
LEY DE GAUSS EN FORMA DIFERENCIAL
La relación anterior, puede generalizarse de inmediato al caso de una distribución continua de carga encerrada por una superficie de forma arbitraria cerrada, al igual que antes, la sumatoria sobre las N cargas la reemplazamos por la integral extendida sobre todo el volumen que contiene a la carga. La nueva expresión para el flujo eléctrico será:
![]()
.....(16)
Recordemos ahora el teorema de la divergencia.
Teorema de la divergencia
“La integral de la divergencia de un vector sobre un volumen V es igual a la integral de superficie de la componente normal del vector sobre la superficie que limita V”, así:
![]()
En nuestro caso, tomando el vector ![]()
como el campo eléctrico:
![]()
.....(17)
A partir de las relaciones (16) y (17), obtenemos:
![]()
.....(18)
Esta ecuación es válida para cualquier elección del volumen y la única forma de que esto sea cierto es que:
![]()
.....(19)
Esto se conoce como la ley de Gauss para el campo eléctrico en forma diferencial.



O
+q
O
-q

Fig. 09. N cargas puntuales encerradas por una superficie cerrada de forma arbitraria
Descargar
| Enviado por: | EDGAR RONAL |
| Idioma: | castellano |
| País: | Perú |
