Equipos e instalaciones electrotécnicas
Campo creado por un solenoide
Campo creado por un solenoide
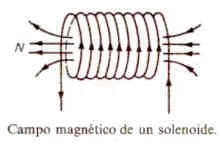
El campo magnético creado por un solenoide tiene las líneas de fuerza en su interior, son perpendiculares al plano de la espira y cerradas sobre sí mismas Fig. izq.
De acuerdo con la regla de la mano derecha, para determinar el sentido del vector inducción, bastara coger la espira en uno cualquiera de sus puntos con el dedo pulgar señalando el sentido de la corriente y verificar el giro de los restantes dedos de la mano.
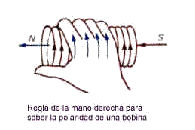
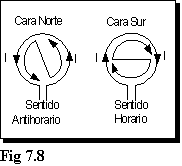
Ese será el sentido del vector inducción. Puesto que una corriente eléctrica se comporta de forma similar a un imán, vamos a ver como pueden determinarse sus polos magnéticos para el caso de una espira, solenoide, etc. Como regla general puede establecerse que en toda espira, si la corriente que la recorre tiene sentido antihorario cuando se la observa frontalmente, esa cara es NORTE, en tanto si el sentido de circulación es horario, la cara que presenta es SUR. La Fig. 7.8 aclara lo expuesto.
Nuestro objetivo va un poco más lejos, pues queremos determinar el valor del módulo del vector inducción en el centro de la espira. De la fórmula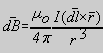
, teniendo en cuenta que los vectores y son perpendiculares en todo punto de la espira y que el radio de la misma es R, puede escribirse:
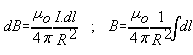
que integrada a lo largo del perímetro de la circunferencia resulta:
![]()
Si se trata de una bobina de N espiras muy próximas entre sí de radio medio R, la inducción magnética en su centro es:
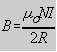
Puede extenderse esta expresión para el cálculo de la inducción magnética en puntos del eje de simetría de un solenoide (bobina) de gran longitud ( l»R). Si está formado por N espiras, su longitud es l y su radio R, verificándose entre estos dos últimos la anterior condición, resulta:
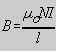

Para un solenoide que no cumpla lo anteriormente establecido (l»R), el valor de la inducción para un punto P de su eje e interior a él (Fig 8.8) es:

expresión que coincide con la (10) si ![]()
.(Solenoide de gran longitud).

Descargar
| Enviado por: | Miguel Campo |
| Idioma: | castellano |
| País: | España |
