Matemáticas
Cálculo de la matriz inversa
Cálculo de la matriz inversa usando determinantes
Dada una matriz cuadrada A, se llama matriz adjunta de A, y se representa por Adj(A), a la matriz de los adjuntos, Adj(A) = (Aij).
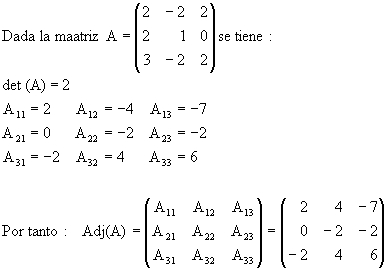
Si tenemos una matriz tal que det (A) ¹ 0, se verifica:
![]()
Esto es fácil probarlo puesto que sabemos que la suma de los productos de los elementos de una fila por sus adjuntos es el valor del determinante, y que la suma de los productos de los elementos de una fila por los adjuntos de otra fila diferente es 0 (esto sería el desarrollo de un determinante que tiene dos filas iguales por los adjuntos de una de ellas).
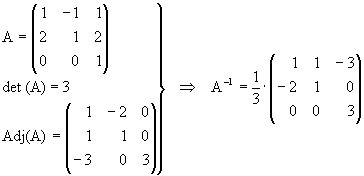
Método de Gauss-Jordan para el cálculo de la matriz inversa
El método de Gauss - Jordan para calcular la matriz inversa de una dada se basa en una triangularización superior y luego otra inferior de la matriz a la cual se le quiere calcular la inversa.
![]()
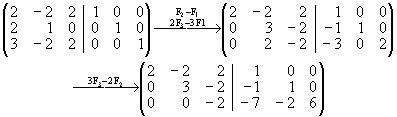
Para aplicar el método se necesita una matriz cuadrada de rango máximo. Sabemos que no siempre una matriz tiene inversa, por lo cual comprobaremos que la matriz tenga rango máximo al aplicar el método de Gauss para realizar la triangularización superior. Si al aplicar el método de Gauss (triangularización inferior) se obtiene una línea de ceros, la matriz no tiene inversa.
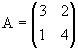
Descargar
| Enviado por: | José Ríos Saldaña |
| Idioma: | castellano |
| País: | México |
