Ingeniero Técnico Industrial
Biela-manivela: Problema dinámico-inverso
PRÁCTICA DE TEORÍA DE MÁQUINAS
Mecanismo 3. Biela-Manivela. Introducción.
En este mecanismo, el movimiento de rotación de una manivela o cigüeñal provoca el movimiento rectilíneo, alternativo, de un pistón o émbolo. Una biela sirve para unir las dos piezas. Con la ayuda de un empujón inicial o un volante de inercia, el movimiento alternativo del pistón se convierte en movimiento circular de la manivela. El movimiento rectilíneo es posible gracias a una guía o un cilindro, en el cual se mueve. Este mecanismo se usa en los motores de muchos vehículos.
El recorrido máximo que efectúa el pistón se llama carrera del pistón. Los puntos extremos del recorrido corresponden a dos posiciones diametralmente opuestas de la manivela. Por lo tanto, el brazo de la manivela (distancia del eje al punto de unión con la biela) equivale a la mitad de la carrera del pistón.
El pistón completa dos carreras por cada vuelta de la manivela, de manera que la relación entre velocidades es
Vm = 2 ð R / ð
donde
Vm : velocidad media del pistón
ð : velocidad de giro de la manivela
R : brazo de la manivela
El cálculo de la velocidad máxima que adquiere el pistón es más complicado, y depende básicamente de la longitud de la biela. Cuando la biela es bastante mayor que el brazo de la manivela, la máxima velocidad se produce aproximadamente a medio recorrido, y toma por valor
VM = ð R
donde
VM : velocidad máxima del pistón
PROBLEMA CINÉMATICO.
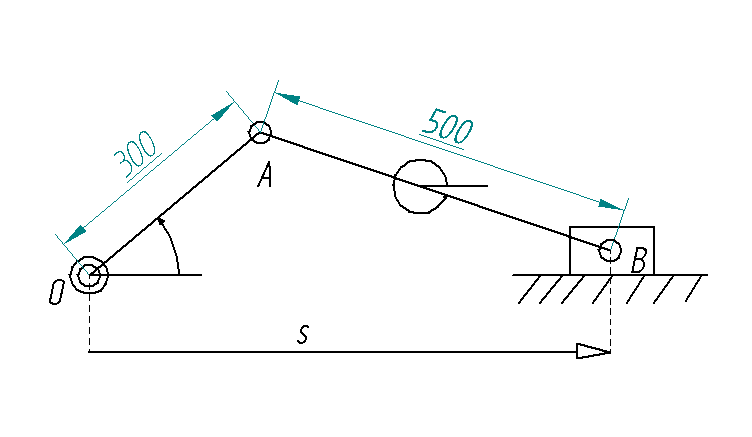
El problema cinématico consiste en conocer las posiciones, velocidades y aceleraciones de todas las barras, esto lo voy a hacer mediante tres pasos, primero resolveré el problema de posición para pasar después al problema de velocidad y por ultimo resolveré el problema de aceleración. Representaré gráficamente la evolución frente al tiempo de posición, velocidad y aceleración de la barra de salida en mi caso la corredera del mecanismo biela manivela.
Problema de posición:
El problema de posición lo resuelvo empleando las ecuaciones de lazos, así el lazo que uso es:
Tomando las cotas en centímetros, las pasamos a metros.
![]()
Con lo que tengo un sistemas de dos ecuaciones con dos incógnitas, resolviéndolo obtengo, s y ,
Del que obtengo: (1)
(2)
En los datos de la practica se dicen que la barra de entrada evoluciona con velocidad constante durante el recorrido considerado, por tanto
Dando valores numéricos, de lo que sacamos que:
Representando gráficamente la posición del barra de salida; s frente t.
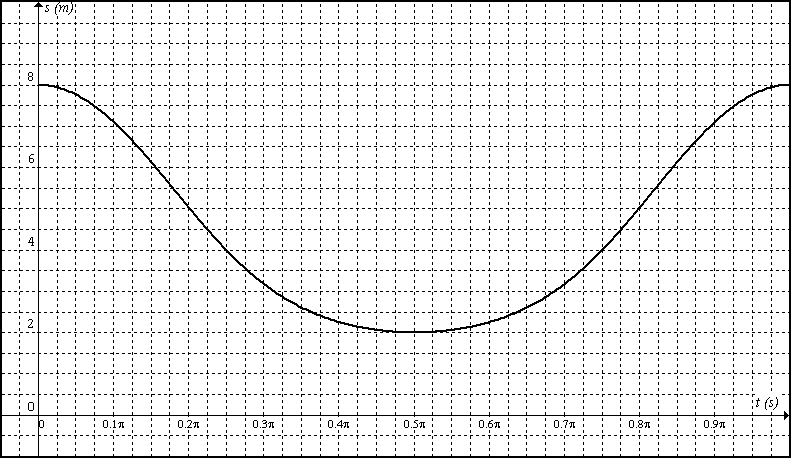
3cos(2x)+5cos(asen(-0.6sin(2x)))
Problema de velocidad
Derivando las ecuaciones de lazo del problema de posición obtenemos la solución del problema de velocidad, aunque también podríamos obtener las velocidades derivando las expresiones (1) y (2) directamente, pero he usado la primera opción:
Valores numéricos:
Resolviendo llegamos: (3)
(4)
Representando gráficamente frente a t
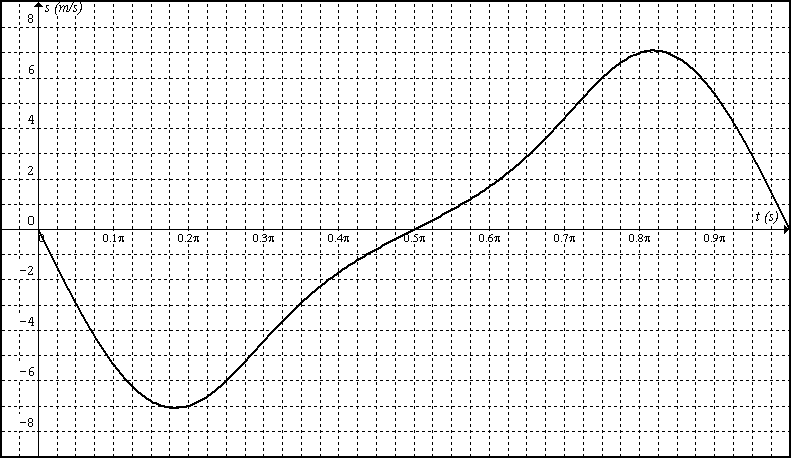
-6sin(2x)+6cos(2x)*tan(asen(-0.6sin(2x)))
Problema de aceleración.
Derivando las ecuaciones del problema de velocidad obtenemos la solución del problema de aceleración, aunque también podríamos obtener las aceleraciones derivando las expresiones (3) y (4) directamente, pero otra vez he usado la primera opción:
Con lo que del sistema de ecuaciones sacamos:
(5)
(6)
con:
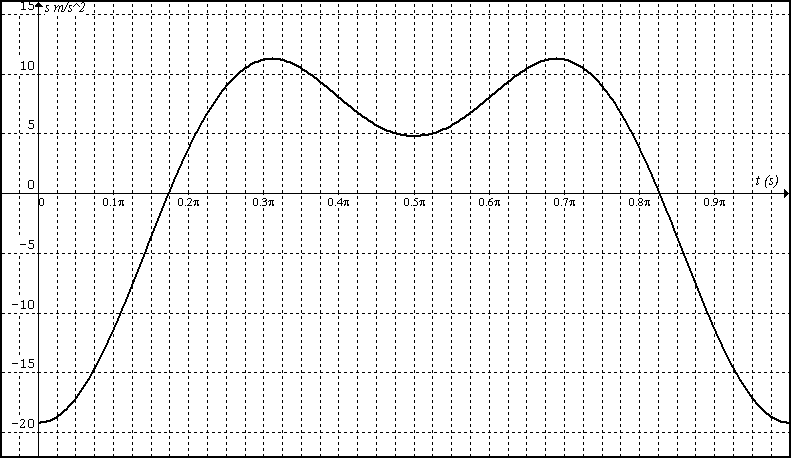
-12cos(2x)-7.2 ((cos(2x))^2)/cos(asen(-0.6sin(2x)))-tan(asen(-0.6sin(2x)))*(12sin(2x)+4.32sin(2x)*(cos(2x)/cos(asen(-0.6sin(2x))))^2)
Problema Dinámico Inverso.
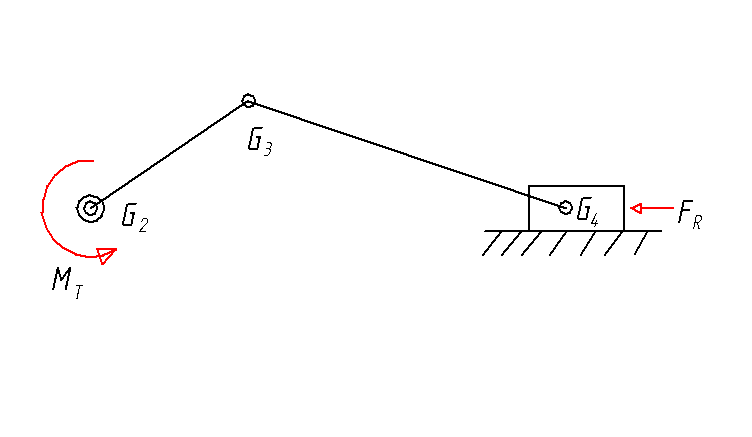
Las condiciones para que actúe la fuerza resistente F son: 5<s<8 y que la velocidad de la corredera sea positiva, esto se cumple pata t>2,5 s, así pues la fuerza resistente actuará en el intervalo de tiempo 2,5<t<3.14 s
Tomando los centros de gravedad como se indica en la figura y las masas de todos los cuerpos como 1 Kg:
Energía potencial:
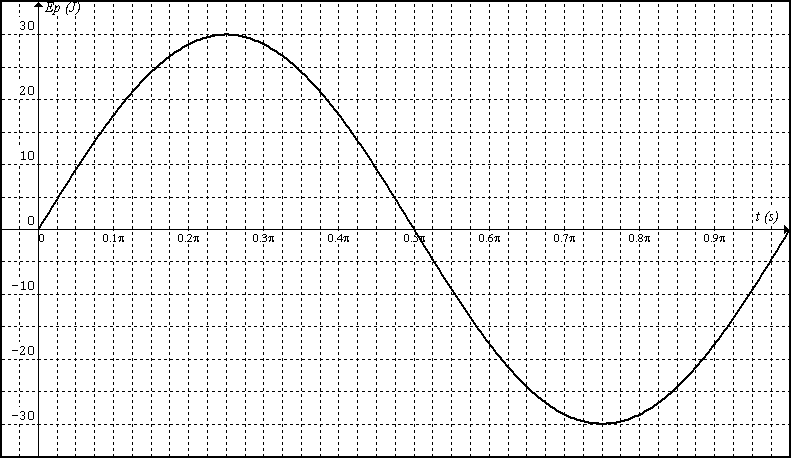
30sen(2x)
Energía cinética: Tomamos las inercias respecto a los centros de gravedad 0,1
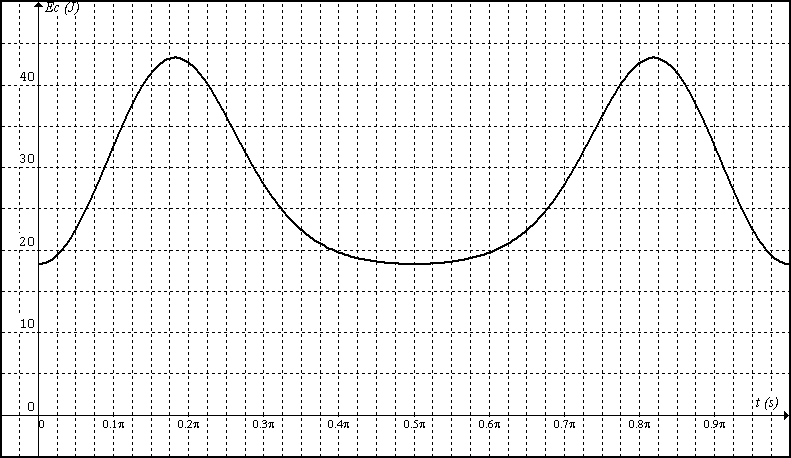
0.2+0.05 (-1.2cos(2x)/cos(ase(-0.6sen(2x))))^2+18+0.5(-6sen(2x)+6cos(2x)*tan(ase(-0.6sen(2x))))^2
Trabajo fuerza resistente:
=
W=(3cos(2t)+5cos(ase(-0.6sen(2t)))-5)*1000
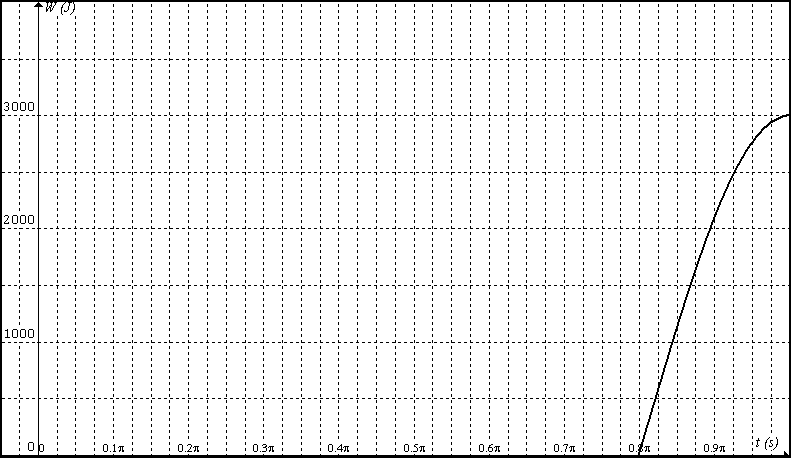
Cálculo de T: Usando el PPV.
Cálculos previos:
Para t<2,5 s
T=30cos(2t)+ +0.5()
Para t>2,5 s
T=30cos(2t)+ +0.5(+1000)
Representándolo en una sola gráfica queda:
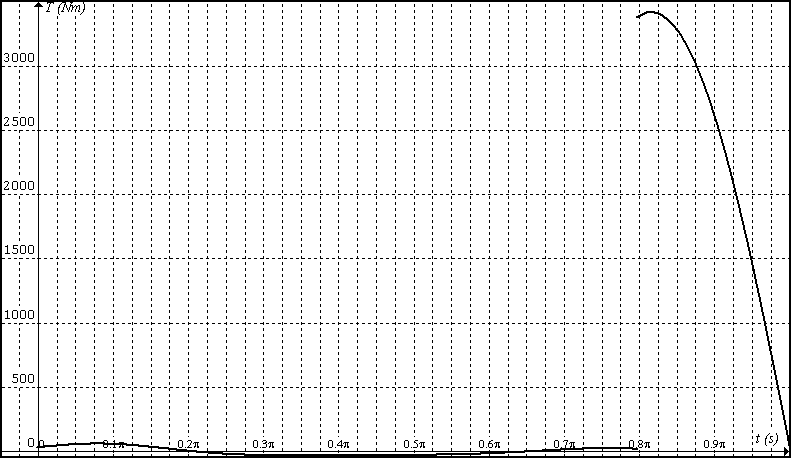
Trabajo del par motor
pero como para s actúa F tenemos que particionar la integral.
=
Descargar
| Enviado por: | Oscar Linares Vita |
| Idioma: | castellano |
| País: | España |
