Informática
Aproximación por mínimos cuadrados
APROXIMACIÓN POR MÍNIMOS CUADRADOS
Es conocido que cuando realizamos cualquier medición, estamos cometiendo errores de diferente indole según la magnitud de medida del instrumento utilizado. Por lo tanto los métodos vistos hasta ahora no nos interesan porque nos daban polinomios que pasaban por dichos puntos. Lo que nos interesa ahora el que el error que haya entre los puntos y la hipotética función sea mínima.
Nosotros tenemos (n+1) puntos y tenemos que calcular una función de la cual desconocemos (m+1) parámetros. Los datos que debemos de calcular son las siguientes: a0,a1,a2,...am.
El objetivo que nosotros perseguiremos será la de minimizar la suma del cuadrado de las distancias desde la f(x) hasta los puntos. Utilizando una expresión matemática nos quedará de la siguiente manera:
![]()
Mediante la wi (i=1,2,3..n) nos permite introducir en la función valores que nos permitirán variar el grado de importancia que tienen los distintos datos. En el caso de que no se aprecie variación en las importancias, la w será 1
Para llegar al caso general utilizaremos el caso de líneas rectas.
P1(x)=a0+a1x donde a0 y a1 se eligen de tal manera que la suma de los cuadrados minimice el error de todos los datos. Lo ahora mencionado lo podemos representar de la siguiente forma:
![]()
Para que tengamos unos mínimos deberemos derivarlo con respecto a0 y a1, realizando algunas simplificaciones después para que el resultados sea más visual. Estas son las ecuaciones obtenidas:
![]()
![]()
Consideraremos que el factor de importancia w es igual para todos los casos, siendo entonces su valor 1. Las ecuaciones anteriormente escritas las podemos representar mediante la siguiente matriz:
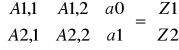
A continuación explicaremos que es cada elemento de la matriz:
![]()
![]()
![]()
![]()
![]()
Lo que deberíamos hacer a continuación sería resolver los valores de a0 y a1 lo cual no tiene ningún misterio.
A partir del caso de líneas rectas ahora podemos generalizar para un conjunto de n datos. Siguiendo los mismos pasos que para el caso de líneas rectas, obtendremos la expresión que minimice la suma de los cuadrados de las distancias de error de todos los datos, derivandolo a continuación con respecto a0,a1,...am.
Desarrollando estas ecuaciones obtendremos el siguiente sistema de ecuaciones:
![]()
![]()
... ... ... ...
![]()
Ahora tenemos un sistema de m+1 ecuaciones lineales, para m+1 coeficientes a0,a1,a2...am (las incognitas) siendo m el grado de la misma.
Se puede deducir que los coeficientes son: ![]()
Siendo los términos independientes:![]()
A continuación introduciremos el programa que utilizaremos para resolver los ejercicios de aproximación por mínimos cuadrados.
PROGRAMA
program min_cuad;
const
limite=7;
type
matriz=array [1..limite+1,1..limite] of real;
var
m:matriz;
procedure introducir_datos (var m:matriz);
var
i:integer;
begin
for i:=1 to limite do
begin
writeln ('Introduce el valor de x',i,':');
readln (m[1,i]);
writeln ('Introduce el valor de y',i,':');
readln (m[2,i]);
end;
end;
procedure calcular (var m:matriz);
var
i:integer;
a12,z1,a22,z2,a11,d,a0,a1:real;
begin
for i:=1 to limite do
begin
m[3,i]:=m[1,i];
m[4,i]:=m[2,i];
m[5,i]:=sqr(m[1,i]);
m[6,i]:=(m[1,i]*m[2,i]);
writeln ('Introduce la influencia del punto ',i);
readln (m[7,i]);
end;
a12:=0;
z1:=0;
a22:=0;
z2:=0;
a11:=0;
for i:=1 to limite do
begin
a11:=a11+(m[7,i]);
a12:=a12+(m[3,i]*m[7,i]);
z1:=z1+(m[4,i]*m[7,i]);
a22:=a22+(m[5,i]*m[7,i]);
z2:=z2+(m[6,i]*m[7,i]);
end;
d:=(a11*a22)-(a12*a12);
a0:=((a22*z1)-(a12*z2))/d;
a1:=((a11*z2)-(a12*z1))/d;
writeln ('P(x)= ',a0,'+',a1,'x');
end;
begin
introducir_datos (m);
calcular (m);
end.
DATOS: 1
| i | x | y | w |
| 1 | 0.1 | 0.61 | 1 |
| 2 | 0.4 | 0.92 | 1 |
| 3 | 0.5 | 0.99 | 1 |
| 4 | 0.7 | 1.52 | 1 |
| 5 | 0.7 | 1.47 | 1 |
| 6 | 0.9 | 2.03 | 1 |
Como resultado hemos obtenido, un polinomio de primer grado, siendo su valor: 0.28616033755+1.764556962x
DATOS:2
| i | w | x | y |
| 1 | 1 | -5 | 18 |
| 2 | 1 | -3 | 7 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 3 | 7 |
| 5 | 20 | 4 | 16 |
| 6 | 1 | 6 | 50 |
| 7 | 1 | 8 | 67 |
El polinomio obtenido a partir de los datos introducidos ha sido: 8.8990918264+2.6402623613x
Para el caso en el cual el grado del polinomio es superior a uno, mediante el programa que viene a continuación realizariamos la colocación en la matriz de los datos y utilizando el método de Gauss realizariamos los cálculos de a , y .
PROGRAMA
program min_cua2;
const
limite1=11;
limite2=7;
fila=3;
columna=4;
type
matriz=array [1..limite1,1..limite2] of real;
matriz1=array [1..fila,1..columna] of real;
var
m:matriz;
m1:matriz1;
i,j:integer;
procedure introducir_datos (var m:matriz);
var
i:integer;
begin
for i:=1 to limite2 do
begin
writeln ('Introduce el valor de x',i,':');
readln (m[1,i]);
writeln ('Introduce el valor de y',i,':');
readln (m[2,i]);
writeln ('Introduce el valor de w',i,':');
readln (m[3,i]);
end;
end;
procedure calcular (var m:matriz;var m1:matriz1);
var
i:integer;
a11,a12,a22,a23,a33,z1,z2,z3:real;
begin
for i:=1 to limite2 do
begin
m[4,i]:=m[3,i];
m[5,i]:=m[1,i];
m[6,i]:=sqr (m[1,i]);
m[7,i]:=m[6,i]*m[1,i];
m[8,i]:=sqr (m[6,i]);
m[9,i]:=m[2,i];
m[10,i]:=m[1,i]*m[2,i];
m[11,i]:=m[6,i]*m[2,i];
end;
a11:=0;
a12:=0;
a22:=0;
a23:=0;
a33:=0;
z1:=0;
z2:=0;
z3:=0;
for i:=1 to limite2 do
begin
a11:=a11+m[4,i];
a12:=a12+(m[3,i]*m[5,i]);
a22:=a22+(m[3,i]*m[6,i]);
a23:=a23+(m[3,i]*m[7,i]);
a33:=a33+(m[3,i]*m[8,i]);
z1:=z1+(m[3,i]*m[9,i]);
z2:=z2+(m[3,i]*m[10,i]);
z3:=z3+(m[3,i]*m[11,i]);
end;
m1[1,1]:=a11;
m1[1,2]:=a12;
m1[1,3]:=a22;
m1[1,4]:=-z1;
m1[2,1]:=a12;
m1[2,2]:=a22;
m1[2,3]:=a23;
m1[2,4]:=-z2;
m1[3,1]:=a22;
m1[3,2]:=a23;
m1[3,3]:=a33;
m1[3,4]:=-z3;
end;
begin
introducir_datos (m);
calcular (m,m1);
for i:=1 to fila do
begin
for j:=1 to columna do
write (m1[i,j],' ');
writeln;
end;
end.
DATOS:3
| i | w | x | y |
| 1 | 1 | -5 | 18 |
| 2 | 1 | -3 | 7 |
| 3 | 1 | 1 | 0 |
| 4 | 1 | 3 | 7 |
| 5 | 20 | 4 | 16 |
| 6 | 1 | 6 | 50 |
| 7 | 1 | 8 | 67 |
Si quisieramos realizar un polinomio de grado 2, mediante el procedimiento anterior, obtendriamos la siguiente matriz:
Una vez de obtener esta matriz, utilizando el método de Gauss obtendremos los valores , y siendo la ecuación:
-3.4079+0.6964+1.0667
1
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | España |
