Matemáticas
Aplicaciones de la integral definida
Tutoría de matemáticas
Investigar las definiciones y formulas de las principales aplicaciones de la integral definida:
Integral Definida.
![]()
Definición de integral definida; La integral (denominada algunas veces la integral definida) de una función f(x). Entre x = a y x = b, se escribe como:
Inclusive, se interpreta como el área de la región limitada por la gráfica y = f(x) el eje “x” y las líneas verticales de x = a, y x = b (a<b); Si el área esta por encima del eje “x”, es positiva y si esta por debajo del eje “x”, es negativa.
y
y = f(x)
+ x
( - )
Coeficientes de desigualdad para distribución de ingreso
La curva de Lorenz se utiliza en la economía y ecología para describir la desigualdad de abundancia o tamaño. La curva de Lorenz es una función de la proporción acumulativa de individuos pedidos tras sobre la proporción acumulativa correspondiente de su tamaño. Dado una muestra de n pidió a individuos con el tamaño del individuo i y,
después está el polígono la curva de Lorenz de la muestra que
ensambla los puntos, donde h = 0, 1, 2… n, y Alternativamente, la curva de Lorenz se puede expresar como donde está la función de distribución acumulativa de individuos pedidos y es el medio F(y) clasificar.
Si todos los individuos son del mismo tamaño, la curva de Lorenz es una línea diagonal recta, llamada la línea de la igualdad. Si hay alguna desigualdad de tamaño, entonces la curva de Lorenz cae debajo de la línea de la igualdad. La cantidad total de desigualdad se puede resumir por el coeficiente de Gini (también llamado el cociente de Gini), que es el cociente entre el área incluida por la línea de la igualdad y la curva de Lorenz, y el área triangular total bajo línea de la igualdad. El grado de la asimetría alrededor del eje de la simetría es medido por el coeficiente supuesto de la asimetría de Lorenz
-
Ejercicio
Encuentre el coeficiente de desigualdad de la distribución de ingreso dada por la curva ![]()
, en donde X es la proporción acumulada de captadores de ingresos y Y es la proporción acumulada del ingreso nacional.
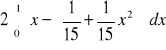
![]()
![]()
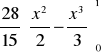
![]()
![]()
![]()
R//
Curvas de aprendizaje
Las curvas de aprendizaje, también llamadas economías de escala dinámicas, hacen referencia al aumento de la productividad que se produce a través de la experiencia acumulada. Cuando una empresa lleva más de un periodo produciendo un bien aprende a producirlo mejor, se hace con el know how del proceso productivo, lo que se traduce en una disminución del coste unitario a medida que aumenta la producción acumulada.
La importancia de esta relación puede llevar a que determinadas empresas produzcan más que la cantidad de equilibrio durante los primeros periodos con el fin de bajar por su curva de aprendizaje más rápidamente que sus competidores, es decir, para crear una barrera de entrada.
Formula
![]()
-
Ejercicio
Después de observar las primeras 400 unidades de su producto, una empresa determina que el tiempo de mano de obra requerido a fin de ensamblar la unidad (x+1) fue de
![]()
. Calcule el total de horas de mano de horas requeridas con el objeto de producir 500 unidades adicionales
![]()
![]()

![]()
![]()
![]()
10000 R//
Maximización de la utilidad con respecto al tiempo
En ciertas empresas como la explotación de minas, se tornan no rentables con el tiempo. En tales operaciones, la tasa de ingreso R´(t) puede ser muy alta al inicio de la operación pero puede decrecer a medida que transcurre el tiempo debido al agotamiento de recursos. La tasa de costo C´(t) es pequeña al principio , pero se incrementa con el tiempo por costo de extracción mas altos ,etc. En tales operaciones existe un instante en el que el administrador debería cerrar la fabrica antes de perder dinero, lo que resultaría en la utilidad máxima obtenida.
Formula
![]()
-
Ejercicio
La función costo marginal e ingreso marginal, de una empresa y , en donde X denota el # de unidades producidas y los costos fijos son de 25$
Encuentre el nivel de producción que maximizaría las utilidades de la empresa.
Calcule la utilidad total de la empresa con este nivel de producción
Determine la utilidad si el nivel de producción se incrementa en 2 unidades, mas allá del nivel de utilidad máxima
I´(x)=C´(x) U = I - C
x=-8 x=4 r //

= 74.6 r//


-72-72+192 = 48r//
Valor presente de un ingreso continuo
Donde un ingreso esta repartido a lo largo de un numero de años futuros , a veces es útil calcular el valor presente de este ingreso. Esto puede ser particularmente valioso cuando una compañía tiene que elegir entre tasas alternativas para explotar recursos.
Como en estos casos el ingreso se obtiene continuamente sobre un periodo, es necesario utilizar descuentos continuos para calcular el valor presente.
Formula
VP =
-
Ejercicio
Una inversión inicial de P dólares, crece continuamente a una tasa anual del 6%. Si la inversión tiene un valor de 26997 $ después de 5 Años, determina la inversión inicial
u = -0.06t
du = -0.06dt
(-33333.1)-(-449950)
116618.85 r//
Superávit del consumidor y del productor
El superavit de los consumidores esta dado por el área entre la curva de demanda p = F(x) y la línea horizontal P = Po
En un mercado de libre competencia existen también productores que estarían dispuestos a vender el articulo a un precio menor que el de los productores también se benefician: este beneficio de los productores se denomina el superávit de los productores.
Formula
SC = ![]()
SP = ![]()
-
Ejercicio
No existe demanda para una nueva marca de filmadoras, si el precio por cámara es de 1700$ o mas, por cada disminución de 100 $ en el precio la demanda se incrementará en 200 unidades. El fabricante no esta dispuesto a considerar un precio unitario de 500 $ para empezar su oferta, y ofrecerán 1400 cámaras a un precio de 850 $
Determine las ecuaciones de ofertas y demandas
Cual es la cantidad y precio de equilibrio
Cuanto están dispuestos a gastar los consumidores por el producto
Determine el superávit del consumidor y del productor para el caso
Demanda ferta
P Q P Q
1600 200 500 0
1700 0 850 1400
![]()
*![]()
*![]()
*![]()
*![]()
*![]()
*![]()
*![]()
*![]()
R//
*![]()
R//
![]()
-0.5x-0.25x=500-1700
(-) -0.75x=-1200
x=1600 R//
p=900 R//
![]()
![]()
![]()
-2560000+2720000
160000 R//
SC= SP =
![]()
![]()





1440000-320000-800000
320000 R//
-640000+2720000-1440000
640000 R//
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Descargar
| Enviado por: | Juan Carlos |
| Idioma: | castellano |
| País: | Ecuador |
