Estadística
Análisis estadístico
Unidad I: Distribución de Probabilidades
Experimento Aleatorio
Un experimento es un proceso de observación de sucesos y del cual se desconoce su ocurrencia.
Ejemplo, Se observa el número de personas que fuman mientras manejan, en la ave. 27 de Febrero.
Espacio Muestral
El espacio muestral es el conjunto de todos los resultados posibles.
Ejemplo, El espacio muestral si lanzamos un dado es el siguiente:
{1,2,3,4,5,6}
Eventos o Sucesos
Un evento es uno o más de los resultados posibles de hacer algo.
Ejemplo, cuando se tira el dado cae en la cara 1.
Los eventos pueden ser mutuamente excluyentes, que es cuando solo uno de ellos puede tener lugar a un tiempo, y no mutuamente excluyente.
Variable Aleatoria
Se llama así cuando toma diferentes valores como resultado de un experimento aleatorio. Puede ser discreta o continua.
Es discreta cuando toma un número limitado de valores, sin embargo, es continua cuando toma cualquier valor dentro de un intervalo determinado.
Ejemplos:
El número de niñas que nacen en la clínica San Rafael semanalmente va desde 2 a 10.
El número de mujeres atendidas en un día en la Clínica San Rafael.
Distribución de Probabilidades
Es una lista de los resultados de un experimento con las probabilidades que se esperarían ver asociados con cada resultados. Pueden ser al igual que las variables discretas o continuas.
Peso | Niño | Niña |
5,8 |
|
|
5,9 |
|
|
6 |
|
|
6,1 |
|
|
6,2 |
|
|
6,3 |
|
|
6,4 |
|
|
6,5 |
|
|
6,6 |
|
|
Valor Esperado o Esperanza matemática
Es el promedio pesado de los resultados de un experimento. Para obtenerlo se multiplica cada valor que la variable puede tomar por la probabilidad de ese valor y se suman los productos. El valor esperado es un solo número.
Ejemplo,
Valores Posibles | Probabilidad | Valor Esperado |
1 | 0.0476 | 0.0476 |
2 | 0.0952 | 0.1904 |
3 | 0.1429 | 0.4287 |
4 | 0.1905 | 0.7620 |
5 | 0.2381 | 1.1905 |
6 | 0.2857 | 1.7142 |
21 | 1 | 4.3334 |
Desviación Standard
Representa el alejamiento de una serie de números de su valor medio. Se calcula a partir de todas las desviaciones individuales con respecto a la media. La desviación estándar es la raíz de la varianza.
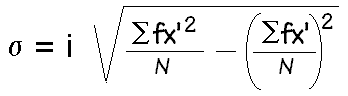
La desviación estandar nos permite determinar donde están localizados los valores en una distribución con relación a la media.
Distribución Binomial
Es una distribución discreta que describe los resultados de un experimento conocido como proceso Bernoulli.
Las características de una distribución binomial son las siguientes:
cada intento tiene solo 2 resultados posibles.
La proporción de éxito permanece fijo con respecto al tiempo
Cada intento es independiente.
La fórmula para las distribuciones binomiales es la siguiente:
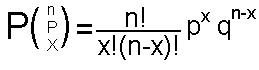
En un partido de football, hay un 20% de que a algun jugador obtenga una tarjeta amarilla, y 80% de que no.
Cual el la probabilidad de que de 10 jugadores nadie obtenga una tarjeta amarilla?
Datos Procedimientos Significa
P= 0.20 La probabilidad que nadie obtenga
Q= 0.80 tarjeta amarilla es de 10.73%
N= 10
Distribución de Poisson
Es una distribución discreta en la que la probabilidad de presentación de un evento en un intervalo es muy pequeño, es un número también muy pequeño.
Su formula es
Distribución Normal
Es una distribución cuya curva tiene un solo pico, es unimodal, y debido a su simetría, la mediana y la moda se encuentran en el centro. Además sus dos extremos se extienden indefinidamente.
La distribución se emplea cuando la variable aleatoria sea continua o n tienda a ser grande.
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | República Dominicana |
