Matemáticas
Álgebra
23. Construir la tabla de la verdad de las siguientes expresiones:
![]()
y demostrar dicha igualdad.
24. Aplicando los teoremas del álgebra de Boole. Simplifique la siguiente
función:
![]()
25. Efectúe la representación por bloques de la siguiente función
booleana:
![]()
26. Simplifique la siguiente función utilizando los teoremas del álgebra de
Boole:
![]()
27. Construya el circuito de la función del ejercicio anterior.
28. Construya el circuito correspondiente a la función booleana del
ejercicio 25.
29. Construya una tabla de la verdad con dos variables booleanas en la
que aparezcan todos los operadores lógicos.
30. Construya el circuito correspondiente a la función:
![]()
31. Demuestre los teoremas de Morgan mediante tablas.
32. ¿Para qué se utiliza el álgebra de Boole en los ordenadores?
33. Calcule las siguientes expresiones.
NOTA: Para las potencias se utiliza el doble asterisco. Así, la base A
elevada al exponente B se escribe así: ![]()
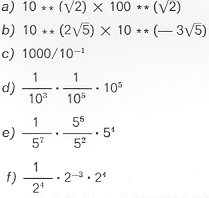
34. Calcule el valor de las siguientes expresiones:

35. Sea un conjunto R formado por los subconjuntos
A={1,2,3} B={4,5,6} y C={0,7,8}
Calcule:
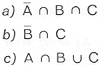
36 Calcule:
a) Log10 1000 + Log10 100
b) Log10 10000 - Log10 1000
37. Demuestre que ![]()
38. Demuestre que
![]()
39. Calcule:
![]()
40. ¿Qué es el conjunto universal?
41. Calcule el valor de log2 10000
42. ¿Cuál es el conjunto de las partes del conjunto X = {2,3,5,7}?
Descargar
| Enviado por: | El remitente no desea revelar su nombre |
| Idioma: | castellano |
| País: | España |
