Informática
Álgebra de Boole y puertas lógicas
Álgebra De Boole
y
Puertas Lógicas
Álgebra De Boole
SUMA
0 + 0 = 0 1 + 1 = 1
0 + 1 = 1 1 + 0 = 1
MULTIPLICACIÓN
![]()
COMPLEMENTACION
![]()
= 1
![]()
= 0
Ejemplo con otros signos:
![]()
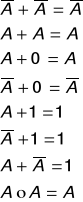
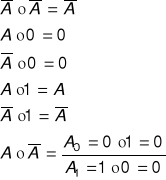
TEOREMA DE MORGAN
![]()
![]()
Ejemplo:
-
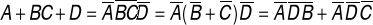
-
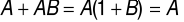
Factor Común
Ejercicios:
Puertas Lógicas
PUERTA NOT O INVERSORA
Se trata de una operación que solo maneja una variable de entrada y otra de salida. La salida toma el estado opuesto o inverso del que tiene la entrada.
![]()
Tabla De La Verdad De La Puerta Inversora NOT
| VALOR EN LA ENTRADA | VALOR EN LA SALIDA |
| 0 | 1 |
| 1 | 0 |
PUERTA OR O SUMADORA
Cuando distintas variables lógicas se combinan mediante la función OR, el resultado toma el estado alto, verdadero o 1 si alguna de ellas tiene dicho estado. La ecuación que representa la función OR de dos variables de entrada es la siguiente:
X = A + B

Tabla De La Verdad De La Puerta Sumadora OR
| VALOR EN LA PARTE A | VALOR EN LA PARTE B | VALOR OBTENIDO EN LA SALIDA |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
PUERTA NOR O SUMADORA INVERSORA
Esta puerta produce la función inversa de la puerta OR, es decir, la negación de la suma lógica de las variables de entrada. Su comportamiento es equivalente a la de la puerta OR seguida de una NOT.
Tabla De La Verdad De La Puerta Sumadora Inversora NOR
| VALOR EN LA PARTE A | VALOR EN LA PARTE B | VALOR OBTENIDO EN LA SALIDA |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
PUERTA AND O MULTIPLICADORA
Cuando varias variables lógicas, de tipo binario, se combinan mediante la operación lógica AND, producen una variable de salida, que solo toma el nivel lógico 1, estado alto o verdadero, si todas ellas tienen dicho nivel o estado. La ecuación lógica de la función AND para dos variables de entrada es la siguiente:

Tabla De La Verdad De La Puerta Multiplicadora AND
| VALOR EN LA PARTE A | VALOR EN LA PARTE B | VALOR OBTENIDO EN LA SALIDA |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
PUERTA NAND O MULTIPLICADORA INVERSORA
La puerta NAND produce la función inversa de la AND, o sea, la negación del producto lógico de las variables de entrada. Actúa como una puerta AND seguida de una NOT.

Tabla De La Verdad De La Puerta Multiplicadora Inversora NAND
| VALOR EN LA PARTE A | VALOR EN LA PARTE B | VALOR OBTENIDO EN LA SALIDA |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
PUERTA OR EXCLUSIVA (OREX)
La salida de esta compuerta es 1, estado alto o verdadero si cada entrada es 1 pero excluye la combinación cuando las dos entradas son 1. La función OR exclusiva tiene su propio símbolo gráfico o puede expresarse en términos de operaciones complementarias AND, OR.

Tabla De La Verdad De La Puerta OR Exclusiva (OREX)
| VALOR EN LA PARTE A | VALOR EN LA PARTE B | VALOR OBTENIDO EN LA SALIDA |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
PUERTA NOR EXCLUSIVA (NOREX)

Tabla De La Verdad De La Puerta NOR Exclusiva (NOREX)
| VALOR EN LA PARTE A | VALOR EN LA PARTE B | VALOR OBTENIDO EN LA SALIDA |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |



Ejercicios:
-
Implementar solo con NAND las puertas: NOT, OR, NOR y AND.

NOT OR

NOR AND


-
Implementar solo con NOR las puertas: NOT, OR, NAND y AND
NOT OR


NAND AND ![]()


-
Implementar solo con NAND la puerta OREX.

-
Implementar solo con NOR la puerta OREX

-
Implementar solo con NAND la puerta NOREX

-
Implementar solo con NOR la puerta NOREX

-
Implementar Y+W con NAND Implementar Y+W con NOR


-
Implementar

con AND

-
Implementar

con NOR

Ejercicios Hoja1:
Obtener simplificada la señal de salida.
Implementar con puertas la salida ya simplificada.
Esquema 1



Implementar con NOR Implementar con NAND

Implementar con las menos puertas posibles



Esquema 2

![]()
Implementar con NOR Implementar con NAND


Implementar con las menos puertas posibles

Esquema 3


Implementar con NOR Implementar con NAND



Esquema 4


![]()
Implementar solo con NOR Implementar solo con NAND


Implementar con las menos puertas posibles

Esquema 5


![]()
Implementar con NOR Implementar con NAND


Esquema 6


Implementar con NOR Implementar con NAND


Esquema 7


Implementar con NOR Implementar con NAND


![]()
![]()
COMPUERTA OREX
A
B
![]()
COMPUERTA NOREX
![]()
MASA (0)
PILA (1)
AL AIRE (1)
![]()
![]()
![]()
![]()
![]()
![]()
A + B
![]()
A + B
![]()
![]()
A B
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A + B
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
YX
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ENTRADA/INPUT
SALIDA/OUTPUT
![]()
Descargar
| Enviado por: | Victor |
| Idioma: | castellano |
| País: | España |







